The Gatlinburg and Householder Symposia
By Cleve Moler, MathWorks
Start MATLAB and issue these commands:
load gatlin image(X) colormap(map)
You will see a photo of the organizing committee for the 1964 Gatlinburg Symposium on Numerical Algebra (Figure 1). If you have been following my blog, you will know that I have written a great deal about the men on this committee. Here, I want to describe the conferences themselves. They have played an important role in the history of MATLAB® and in my own professional life.
In 1961, Gatlinburg was a quiet resort town near the Great Smoky Mountains National Park in eastern Tennessee. Alston Householder, who was in charge of computing at Oak Ridge National Laboratory (ORNL), chose the Mountain View Hotel in Gatlinburg as the site of a week-long research workshop on matrix computations (Figure 2). The town was easy to reach but far from the distractions of a big city. The hotel had excellent facilities for the kind of workshop he had in mind.
In a paper published in SIAM Review, Householder recalled that the suggestion for holding such a meeting had been made a year earlier at the Old German restaurant and pub in Ann Arbor during a University of Michigan summer school session on numerical analysis. Householder formed an organizing committee, which invited about 75 participants. Funding was obtained from the National Science Foundation and the Atomic Energy Commission to support attendees who could not pay their own expenses.
The format for the meeting, repeated in later years, consisted of two or three invited talks in the morning, two or three in the afternoon, and several impromptu, small sessions that ran simultaneously in the evening. Everyone ate in the hotel, and efforts were made to vary the groups of people seated together at each meal.
In 1963, a second meeting was held in Gatlinburg. This one, which focused on approximation theory, was chaired by Frank Olver. The organizers did not know at the time that this meeting was the second in a series, and it wasn’t until some years later that it became known as Gatlinburg II.
My First Meeting
In 1964, a meeting later known as Gatlinburg III was held at the Mountain View Hotel. All six members of the committee—Jim Wilkinson, Wallace Givens, George Forsythe, Alston Householder, Peter Henrici, and Fritz Bauer—had been at the Old German that evening in 1960. I saved the 1964 photo of the group that is now distributed with MATLAB. At the time, I was a Stanford graduate student working for Forsythe. Students had not been invited to previous Gatlinburg meetings. In what had apparently been a contentious move within the committee, Forsythe obtained an invitation for me.
I was the only student at Gatlinburg III. It was enormously important for me to meet the leaders in the field where I would spend most of my professional life.
There have been 16 Gatlinburg meetings since 1964, and I have been to all but one. Originally, the meetings were criticized because attendance was by invitation only from a self-appointed organizing committee. Today, the meetings are still by invitation, but there is now an open application process, and graduate students and other young people are encouraged to apply.
Gatlinburg IV, held in 1969, was the last of the series to take place in Gatlinburg. Householder retired from ORNL and from the conference organizing committee. (Coincidentally, in 1966, I became an assistant professor at the University of Michigan and organizer of the summer school. So it fell to me to invite Householder, Wilkinson, and the others to Ann Arbor, and thus, back to the Old German.)
The Gatlinburg Symposia were on numerical algebra, a topic general enough to allow attendees latitude to talk about their own research. The titles and speakers for some of the presentations at Gatlinburg IV provide a sense of the range of topics covered:
- “Some Basic Results in Automatic Solution of Polynomial Equations,” A. M. Ostrowski
- “Alternating Direction Methods for Galerkin Approximations for Parabolic Problems,” J. Douglas
- “Another Algorithm for Minimizing a Sum of Squares of Nonlinear Functions,” M. J. D. Powell
- “Natural Norms in Algebraic Processes,” V. N. Faddeeva
- “The Ax = λBx and Related Problems,” J. H. Wilkinson
- “Bounds for the Abscissa of Stability of a Stable Polynomial,” P. Henrici
- “The Method of Odd/Even Reduction with Application to Poisson’s Equation,” G. H. Golub
Vera Faddeeva was from the Steklov Institute in what was then called Leningrad. She made the trip at a time when it was not easy for Russians to visit the United States, and was one of several attendees from Eastern Europe. The symposia have always had a rich mix of international participants.
I gave short evening talks on the L-shaped membrane at both Gatlinburg III and IV. Gatlinburg III took place in 1964, when I was still working on my thesis, so the talk was about finite difference methods for the membrane eigenvalues. My thesis, and that talk, used the L-shaped membrane as the archetypical example of a region where the singularity at the 270⁰ corner causes slow convergence of the finite difference eigenvalues.
Gatlinburg IV was in 1969. By then, finite difference methods had been replaced by vastly superior methods that employed expansions in fractional order Bessel functions. These had been described in a 1967 paper by Fox, Henrici, and Moler, but in my Gatlinburg IV talk I was able to describe improvements to the original computational techniques. We use these improved techniques to compute the MathWorks logo today.
A Change of Name and a Change of Venue
The fifth meeting was held in 1972 at Los Alamos National Laboratory in New Mexico, with Richard Varga as the chairman. The present-day pattern for the series began to emerge. The conference is held roughly every three years in venues alternating between Europe and North America. Members of the organizing committee serve limited terms, and the committee itself appoints new members. While the conferences are not formally SIAM activities, SIAM provides logistic and organizational support. At some point, the name of the series changed from the Gatlinburg to the Householder Symposia.
A particularly proud moment in my professional life occurred at Householder V in Los Alamos. For some time before the meeting, Pete Stewart and I had been working on the development of the QZ algorithm for the generalized matrix eigenvalue problem Ax = λBx. The theoretical foundation of the algorithm was Pete’s idea, but we had worked together on the algorithmic aspects and the computer code. Pete was invited to give a talk about our work. Afterwards, Jim Wilkinson stood up and said, “I wish I had thought of that.” It was a wonderful moment.
In 1974, Householder VI was organized by Bauer at the Kurhotel Enzensberg in Hopfen am See, at the foot of the Bavarian Alps. This was the first European meeting in the series.
In 1977, Householder VII, organized by Gene Golub, was held at Asilomar, a spectacular California state park and conference center on scenic 17-Mile Drive on the Monterey Peninsula. The lectures took place in the historic chapel (Figure 3).
Introducing MATLAB
In 1981, Householder VIII, organized by Leslie Fox and Jim Wilkinson, was held in Oxford (Figure 4). (The city of Oxford certainly violates the rule of being isolated from other distractions.) This meeting marks the beginning of the close association between the Householder Symposia and MATLAB that continues to this day.
It was before MathWorks existed. I had installed the code for classic Fortran MATLAB on the mainframe in the campus computer center, and provided show-and-tell from a remote terminal during the coffee breaks and at one of the evening sessions. Some attendees were interested in using the code at their own universities, and so I sent them copies. We can trace many of the early academic adoptions of MATLAB to people who were at this meeting.
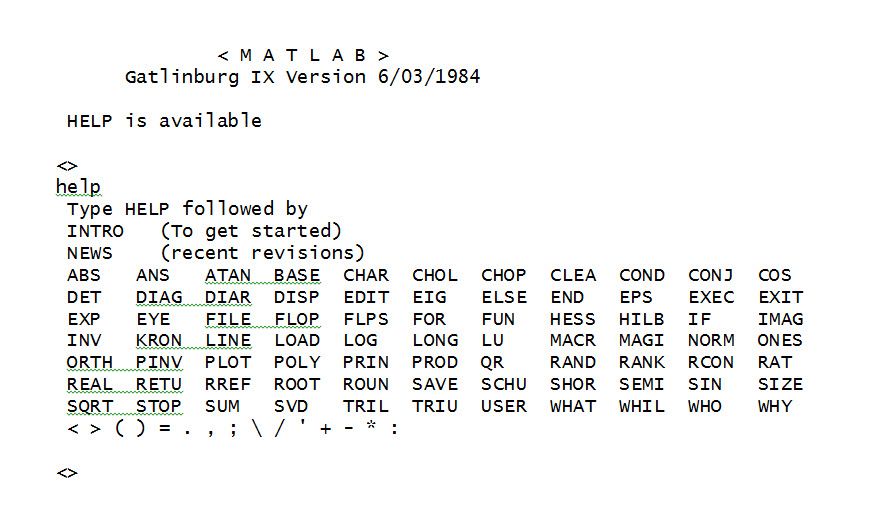
In 1984, Householder IX was organized by Alan George at the University of Waterloo. At the time of this meeting, the IBM PC had been available for over a year. In California, Jack Little was already at work on the MathWorks version of MATLAB, but we could not show that yet. I had ported my Fortran code to the PC. I borrowed a PC AT from Alan, and again, set up near the coffee area. This time, instead of a mag tape with source code, I could promise that a powerful new professional version of MATLAB was on its way.
Figure 5 shows a recreation of what appeared when you started up that classic Fortran MATLAB compiled for Householder IX. There were only 77 functions and keywords. That’s all. There were no M-files, no toolboxes, and only very crude graphics. If you wanted to add new functions, you had to write Fortran subroutines and modify the source code. Basically, MATLAB was just a simple matrix calculator.
In 1987, Householder X was organized by Bob Ward and Pete Stewart and held in Fairfield Glade, Tennessee. Unfortunately, I couldn’t attend. This conference was the only one in the series that I’ve ever missed. It would have been the first at which I could have shown the MathWorks version of MATLAB.
In 1990, Householder XI was organized by Åke Björck and held in Tylösand, on the west coast of Sweden, about 100 miles north of Copenhagen. In an evening talk, I gave a preview of the capabilities for sparse matrices in MATLAB that John Gilbert, Rob Schreiber, and I were then developing. Many of the symposia participants were involved in research on the numerical solution of partial differential equations, and were particularly interested in sparse matrices. We did not have many powerful tools to demonstrate—those would come later—but the idea of having sparse matrices in MATLAB was enthusiastically received.
In 1993, Householder XII was organized by Tony Chan and Gene Golub and held at the UCLA Lake Arrowhead Conference Center in the San Bernardino Mountains, east of Los Angeles. When I demonstrated the latest features of MATLAB at one of the evening sessions, I had some valuable help. Eleven-year-old Tor Bjørstad had come to Lake Arrowhead with his father, Petter, a professor at the University of Bergen in Norway. MATLAB was available on the Bjørstad family computer because Petter had been a fan since his grad student days at Stanford. Tor was a proficient MATLAB user, and so I asked him to operate the computer while I gave the talk. We were listed as co-presenters on the day’s program.
In 1996, 1999, and 2002, there were Householder conferences in Pontresina, Switzerland; Whistler, British Columbia; and Peebles, Scotland, respectively. By this time it would have been presumptuous to give coffee-break demonstrations of MATLAB because almost all the attendees were using MATLAB themselves. Or, at least, their students were. Most of the talks included computational results presented in MATLAB plots. Today, I see MATLAB plots at every conference I attend, but they are more frequent at Householder meetings than at any other.
Announcing Parallel MATLAB
In 2005, Householder XVI was organized by Jesse Barlow and colleagues. It was held at Seven Springs, Pennsylvania, a resort and conference center in the foothills of the Appalachian Mountains, an hour southeast of Pittsburgh. This meeting was particularly significant for me because I made the announcement of parallel MATLAB. Ten years earlier, I had written a one-page Cleve’s Corner article entitled “Why There Isn’t a Parallel MATLAB.” There were three primary reasons:
- Memory model: Matrices are inconsistent with distributed memory.
- Granularity: Efficiency requires large parallel tasks.
- Business situation: The number of users with parallel machines is too small.
This article became one of my most widely cited papers.
My talk at Householder XVI showed how the world of technical computing, and MATLAB, had changed in 10 years. The introduction of distributed arrays provided a much improved memory model. The introduction of the parfor construct provided coarser granularity. By 2005, many MATLAB users had access to parallel computing environments and were anxiously awaiting parallel MATLAB.
In 2008 and 2011, there were Householder conferences in Zeuthen, Germany, and Lake Tahoe, California. In 2014, Householder XIX is being organized by Ilse Ipsen and Paul Van Dooren. It will be held at Domain Sol Cress near the town of Spa in eastern Belgium.
The Gatlinburg and Householder Symposia, 1961–2014
| I | 1961 | Gatlinburg, Tennessee | USA |
| II | 1963 | Gatlinburg, Tennessee | USA |
| III | 1964 | Gatlinburg, Tennessee | USA |
| IV | 1969 | Gatlinburg, Tennessee | USA |
| V | 1972 | Los Alamos, New Mexico | USA |
| VI | 1974 | Hopfen am See | Germany |
| VII | 1977 | Asilomar, California | USA |
| VIII | 1981 | Oxford | England |
| IX | 1984 | Waterloo | Canada |
| X | 1987 | Fairfield Glade, Tennessee | USA |
| XI | 1990 | Tylösand | Sweden |
| XII | 1993 | Lake Arrowhead, California | USA |
| XIII | 1996 | Pontresina | Switzerland |
| XIV | 1999 | Whistler, British Columbia | Canada |
| XV | 2002 | Peebles | Canada |
| XVI | 2005 | Seven Springs, Pennsylvania | USA |
| XVII | 2008 | Zeuthen | Germany |
| XVIII | 2011 | Lake Tahoe, California | USA |
| XIX | 2014 | Spa | Belgium |
Further Reading
Alston S. Householder, “The Gatlinburgs,” SIAM Review 16-3, 1974, pp. 340–343, epubs.siam.org/doi/abs/10.1137/1016054.
Josef Stoer, “The Gatlinburg Symposia and Their Influence on the Development of Numerical Linear Algebra,” IMAGE, The Bulletin of the International Linear Algebra Society 46, 2011, pp. 13–25, www.ilasic.math.uregina.ca/iic/IMAGE/IMAGES/image46.pdf.
Published 2013 - 92138v00