Loma Prieta Earthquake Analysis
This example shows how to store timestamped earthquake data in a timetable and how to use timetable functions to analyze and visualize the data.
Load Earthquake Data
The example file quake.mat contains 200 Hz data from the October 17, 1989, Loma Prieta earthquake in the Santa Cruz Mountains. The data are courtesy of Joel Yellin at the Charles F. Richter Seismological Laboratory, University of California, Santa Cruz.
Start by loading the data.
load quake whos e n v
Name Size Bytes Class Attributes e 10001x1 80008 double n 10001x1 80008 double v 10001x1 80008 double
In the workspace there are three variables, containing time traces from an accelerometer located in the Natural Sciences building at UC Santa Cruz. The accelerometer recorded the main shock amplitude of the earthquake wave. The variables n, e, v refer to the three directional components measured by the instrument, which was aligned parallel to the fault, with its N direction pointing in the direction of Sacramento. The data are uncorrected for the response of the instrument.
Create a variable, Time, containing the timestamps sampled at 200Hz with the same length as the other vectors. Represent the correct units with the seconds function and multiplication to achieve the Hz () sampling rate. This results in a duration variable which is useful for representing elapsed time.
Time = (1/200)*seconds(1:length(e))';
whos TimeName Size Bytes Class Attributes Time 10001x1 80010 duration
Organize Data in Timetable
Separate variables can be organized in a table or timetable for more convenience. A timetable provides flexibility and functionality for working with time-stamped data. Create a timetable with the time and three acceleration variables and supply more meaningful variable names. Display the first eight rows using the head function.
varNames = {'EastWest', 'NorthSouth', 'Vertical'};
quakeData = timetable(Time, e, n, v, 'VariableNames', varNames);
head(quakeData) Time EastWest NorthSouth Vertical
_________ ________ __________ ________
0.005 sec 5 3 0
0.01 sec 5 3 0
0.015 sec 5 2 0
0.02 sec 5 2 0
0.025 sec 5 2 0
0.03 sec 5 2 0
0.035 sec 5 1 0
0.04 sec 5 1 0
Explore the data by accessing the variables in the timetable with dot subscripting. (For more information on dot subscripting, see Access Data in Tables.) Choose the "East-West" amplitude and plot it as function of the duration.
plot(quakeData.Time,quakeData.EastWest)
title('East-West Acceleration')
Scale Data
Scale the data by the gravitational acceleration, or multiply each variable in the table by the constant. Since the variables are all of the same type (double), you can access all variables using the dimension name, Variables. Note that quakeData.Variables provides a direct way to modify the numerical values within the timetable.
quakeData.Variables = 0.098*quakeData.Variables;
Select Subset of Data for Exploration
Examine the time region where the amplitude of the shockwave starts to increase from near zero to maximum levels. Visual inspection of the above plot shows that the time interval from 8 to 15 seconds is of interest. For better visualization draw black lines at the selected time spots to draw attention to that interval. All subsequent calculations involve this interval.
t1 = seconds(8)*[1;1]; t2 = seconds(15)*[1;1]; hold on plot([t1 t2],ylim,'k','LineWidth',2) hold off

Store Data of Interest
Create another timetable with data in this interval. Use timerange to select the rows of interest.
tr = timerange(seconds(8),seconds(15)); dataOfInterest = quakeData(tr,:); head(dataOfInterest)
Time EastWest NorthSouth Vertical
_________ ________ __________ ________
8 sec -0.098 2.254 5.88
8.005 sec 0 2.254 3.332
8.01 sec -2.058 2.352 -0.392
8.015 sec -4.018 2.352 -4.116
8.02 sec -6.076 2.45 -7.742
8.025 sec -8.036 2.548 -11.466
8.03 sec -10.094 2.548 -9.8
8.035 sec -8.232 2.646 -8.134
Visualize the three acceleration variables on three separate axes.
figure subplot(3,1,1) plot(dataOfInterest.Time,dataOfInterest.EastWest) ylabel('East-West') title('Acceleration') subplot(3,1,2) plot(dataOfInterest.Time,dataOfInterest.NorthSouth) ylabel('North-South') subplot(3,1,3) plot(dataOfInterest.Time,dataOfInterest.Vertical) ylabel('Vertical')

Calculate Summary Statistics
To display statistical information about the data use the summary function.
summary(dataOfInterest)
RowTimes:
Time: 1400x1 duration
Values:
Min 8 sec
Median 11.498 sec
Max 14.995 sec
TimeStep 0.005 sec
Variables:
EastWest: 1400x1 double
Values:
Min -255.09
Median -0.098
Max 244.51
NorthSouth: 1400x1 double
Values:
Min -198.55
Median 1.078
Max 204.33
Vertical: 1400x1 double
Values:
Min -157.88
Median 0.98
Max 134.46
Additional statistical information about the data can be calculated using varfun. This is useful for applying functions to each variable in a table or timetable. The function to apply is passed to varfun as a function handle. Apply the mean function to all three variables and output the result in format of a table, because the time is not meaningful after computing the temporal means.
mn = varfun(@mean,dataOfInterest,'OutputFormat','table')
mn=1×3 table
mean_EastWest mean_NorthSouth mean_Vertical
_____________ _______________ _____________
0.9338 -0.10276 -0.52542
Calculate Velocity and Position
To identify the speed of propagation of the shockwave, integrate the accelerations once. Use cumulative sums along the time variable to get the velocity of the wave front.
edot = (1/200)*cumsum(dataOfInterest.EastWest); edot = edot - mean(edot);
Next perform the integration on all three variables to calculate the velocity. It is convenient to create a function and apply it to the variables in the timetable with varfun. In this example, the function is included at the end of this example and is named velFun.
vel = varfun(@velFun,dataOfInterest); head(vel)
Time velFun_EastWest velFun_NorthSouth velFun_Vertical
_________ _______________ _________________ _______________
8 sec -0.56831 0.44642 1.8173
8.005 sec -0.56831 0.45769 1.834
8.01 sec -0.5786 0.46945 1.832
8.015 sec -0.59869 0.48121 1.8114
8.02 sec -0.62907 0.49346 1.7727
8.025 sec -0.66925 0.5062 1.7154
8.03 sec -0.71972 0.51894 1.6664
8.035 sec -0.76088 0.53217 1.6257
Apply the same function velFun to the velocities to determine the position.
pos = varfun(@velFun,vel); head(pos)
Time velFun_velFun_EastWest velFun_velFun_NorthSouth velFun_velFun_Vertical
_________ ______________________ ________________________ ______________________
8 sec 2.1189 -2.1793 -3.0821
8.005 sec 2.1161 -2.177 -3.0729
8.01 sec 2.1132 -2.1746 -3.0638
8.015 sec 2.1102 -2.1722 -3.0547
8.02 sec 2.107 -2.1698 -3.0458
8.025 sec 2.1037 -2.1672 -3.0373
8.03 sec 2.1001 -2.1646 -3.0289
8.035 sec 2.0963 -2.162 -3.0208
Notice how the variable names in the timetable created by varfun include the name of the function used. It is useful to track the operations that have been performed on the original data. Adjust the variable names back to their original values using dot notation.
pos.Properties.VariableNames = varNames;
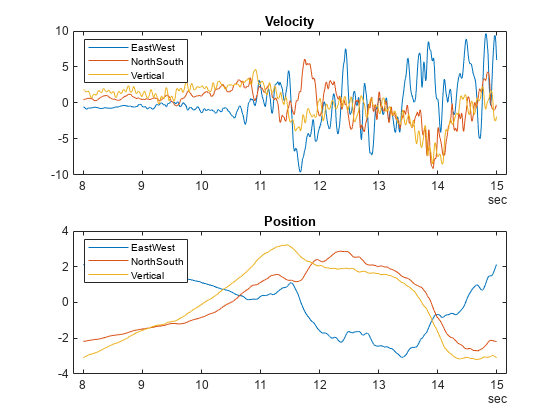
Plot the three components of the velocity and position for the time interval of interest.
figure subplot(2,1,1) plot(vel.Time,vel.Variables) legend(quakeData.Properties.VariableNames,'Location','NorthWest') title('Velocity') subplot(2,1,2) plot(vel.Time,pos.Variables) legend(quakeData.Properties.VariableNames,'Location','NorthWest') title('Position')
Visualize Trajectories
The trajectories can be plotted in 2D or 3D by using the component value. This plot shows different ways of visualizing this data.
Begin with 2-dimensional projections. Here is the first with a few values of time annotated.
figure plot(pos.NorthSouth,pos.Vertical) xlabel('North-South') ylabel('Vertical') % Select locations and label nt = ceil((max(pos.Time) - min(pos.Time))/6); idx = find(fix(pos.Time/nt) == (pos.Time/nt))'; text(pos.NorthSouth(idx),pos.Vertical(idx),char(pos.Time(idx)))

Use plotmatrix to visualize a grid of scatter plots of all variables against one another and histograms of each variable on the diagonal. The output variable Ax, represents each axes in the grid and can be used to identify which axes to label using xlabel and ylabel.
figure [S,Ax] = plotmatrix(pos.Variables); for ii = 1:length(varNames) xlabel(Ax(end,ii),varNames{ii}) ylabel(Ax(ii,1),varNames{ii}) end

Plot a 3-D view of the trajectory and plot a dot at every tenth position point. The spacing between dots indicates the velocity.
step = 10; figure plot3(pos.NorthSouth,pos.EastWest,pos.Vertical,'r') hold on plot3(pos.NorthSouth(1:step:end),pos.EastWest(1:step:end),pos.Vertical(1:step:end),'.') hold off box on axis tight xlabel('North-South') ylabel('East-West') zlabel('Vertical') title('Position')

Supporting Functions
Functions are defined below.
function y = velFun(x) y = (1/200)*cumsum(x); y = y - mean(y); end
See Also
timetable | head | summary | varfun | duration | seconds | timerange
