schur
Schur decomposition
Description
T = schur(A,mode)A is a real matrix, returns a real quasitriangular Schur matrix if mode is
"real" or returns a complex triangular Schur matrix if
mode is "complex". If A is a
complex matrix, then schur returns the complex Schur form regardless of
the value of mode.
[
also returns a unitary matrix
U,T] = schur(___)U such that A = U*T*U'.
Examples
Schur Form of Matrix
Create a 3-by-3 matrix and calculate its Schur form. The result is a matrix with the eigenvalues of A (which are 1, 2, and 3) on the diagonal.
A = [-149 -50 -154; 537 180 546; -27 -9 -25]; T = schur(A)
T = 3×3
1.0000 -7.1119 815.8706
0 2.0000 55.0236
0 0 3.0000
The large off-diagonal elements indicate that this matrix has poorly conditioned eigenvalues, which can be confirmed by finding the condition numbers using the condeig function.
condeig(A)
ans = 3×1
603.6390
395.2366
219.2920
Schur Form of Matrix with Complex Eigenvalues
Create a 3-by-3 matrix with complex eigenvalues.
A = [3 1 1; 0 2 0; -2 1 1]
A = 3×3
3 1 1
0 2 0
-2 1 1
Calculate the real Schur form of A. The 2-by-2 block matrix on the diagonal represents a pair of conjugate complex eigenvalues.
T1 = schur(A)
T1 = 3×3
2.0000 0.3820 1.3764
-2.6180 2.0000 0.3249
0 0 2.0000
Find the eigenvalues of the real Schur form using the ordeig function.
ordeig(T1)
ans = 3×1 complex
2.0000 + 1.0000i
2.0000 - 1.0000i
2.0000 + 0.0000i
Calculate the complex Schur form of A by specifying mode as "complex". The diagonal values of T2 are the eigenvalues of the Schur form of A, which are the same as the output of ordeig.
T2 = schur(A,"complex")T2 = 3×3 complex
2.0000 + 1.0000i 2.2361 + 0.0000i -0.3035 - 0.4911i
0.0000 + 0.0000i 2.0000 - 1.0000i 1.2858 + 0.1159i
0.0000 + 0.0000i 0.0000 + 0.0000i 2.0000 + 0.0000i
Schur Decomposition of Matrix
Create a 3-by-3 magic square matrix and calculate its Schur decomposition factors.
A = magic(3); [U,T] = schur(A)
U = 3×3
-0.5774 -0.8131 -0.0749
-0.5774 0.4714 -0.6667
-0.5774 0.3416 0.7416
T = 3×3
15.0000 0.0000 -0.0000
0 4.8990 -3.4641
0 0 -4.8990
Verify that the norms of A-U*T*U' and U'*U - eye(size(U)) are 0, within machine precision.
norm(A-U*T*U')
ans = 6.7711e-15
norm(U'*U - eye(size(U)))
ans = 5.0471e-16
Input Arguments
A — Input matrix
square matrix
Input matrix, specified as a real or complex square matrix. A
must be dense.
Data Types: single | double
Complex Number Support: Yes
mode — Schur form system
"real" (default) | "complex"
Schur form system, specified as "real" or
"complex".
If
Ais real, thenmodecan be"real"or"complex". Ifmodeis"real", thenschurreturns real quasitriangularT. Ifmodeis"complex", thenschurreturns complex triangularT.If
Ais complex, thenschurignoresmodeand returns the complex Schur form, which is upper triangular with the eigenvalues ofAon the diagonal.
Output Arguments
T — Schur matrix
square matrix
Schur matrix, returned as a real or complex square matrix. If
mode is "complex", then T
is triangular. If mode is "real", then
T is quasitriangular.
More About
Quasitriangular Matrix
An upper quasitriangular matrix can result from the Schur decomposition or generalized Schur (QZ) decomposition of a real matrix. An upper quasitriangular matrix is block upper triangular, with 1-by-1 and 2-by-2 blocks of nonzero values along the diagonal.
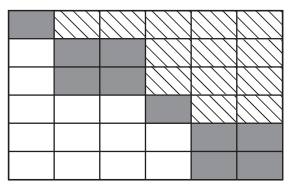
The eigenvalues of these diagonal blocks are also the eigenvalues of the matrix. The 1-by-1 blocks correspond to real eigenvalues, and the 2-by-2 blocks correspond to complex conjugate eigenvalue pairs.
Unitary Matrix
An invertible complex square matrix U is unitary if its conjugate
transpose is also its inverse, that is, if .
Tips
You can use the
rsf2csffunction to convert the real Schur form of a matrix to its complex Schur form.[U,T] = rsf2csf(A)returns the same outputs as[U,T] = schur(A,"complex").
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.
Usage notes and limitations:
Generated code can return a different Schur decomposition than MATLAB® returns.
When the input matrix contains a nonfinite value, the generated code does not issue an error. Instead, the output contains
NaNvalues.Code generation does not support sparse matrix inputs for this function.
Thread-Based Environment
Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool.
This function fully supports thread-based environments. For more information, see Run MATLAB Functions in Thread-Based Environment.
Version History
Introduced before R2006a
Commande MATLAB
Vous avez cliqué sur un lien qui correspond à cette commande MATLAB :
Pour exécuter la commande, saisissez-la dans la fenêtre de commande de MATLAB. Les navigateurs web ne supportent pas les commandes MATLAB.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)