Variable-Displacement Motor
(To be removed) Variable-displacement bidirectional hydraulic motor
The Hydraulics (Isothermal) library will be removed in a future release. Use the Isothermal Liquid library instead. (since R2020a)
For more information on updating your models, see Upgrading Hydraulic Models to Use Isothermal Liquid Blocks.
Libraries:
Simscape /
Fluids /
Hydraulics (Isothermal) /
Pumps and Motors
Description
The Variable-Displacement Motor block represents a device that extracts power from a hydraulic (isothermal liquid) network and delivers it to a mechanical rotational network. The motor displacement varies in proportion to the physical signal input specified at port C or D. The exact port used depends on the block variant selected. See Ports.
Ports A and B represent the motor inlet and outlet, respectively. Port S represents the motor drive shaft. During normal operation, the angular velocity at port S is positive if the pressure drop from port A to port B is positive also. This operation mode is referred to here as forward motor.
Operation Modes

A total of four operation modes are possible. The working mode depends on the pressure drop from port A to port B (Δp), on the angular velocity at port S (ω), and on the instantaneous volumetric displacement of the component (D). The Operation Modes figure maps the modes to the octants of a Δp-ω-D chart. The modes are labeled 1–4:
Mode 1: forward motor — A positive pressure drop generates a positive shaft angular velocity.
Mode 2: reverse pump — A negative shaft angular velocity generates a negative pressure gain (shown in the figure as a positive pressure drop).
Mode 3: reverse motor — A negative pressure drop generates a negative shaft angular velocity.
Mode 4: forward pump — A positive shaft angular velocity generates a positive pressure gain (shown in the figure as a negative pressure drop).
The response time of the motor is considered negligible in comparison with the system response time. The motor is assumed to reach steady state nearly instantaneously and is treated as a quasi-steady component.
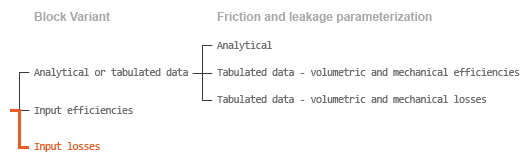
Block Variants and Loss Parameterizations
The motor model accounts for power losses due to leakage and friction. Leakage is
internal and occurs between the motor inlet and outlet only. The block computes the leakage
flow rate and friction torque using your choice of five loss parameterizations. You select a
parameterization using block variants and, in the Analytical or tabulated
data case, the Leakage and friction parameterization parameter.
Loss Parameterizations

The block provides three Simscape™ variants to select from. To change the active block variant, use the Modeling option parameter. The available variants are:
Analytical or tabulated data— Obtain the mechanical and volumetric efficiencies or losses from analytical models based on nominal parameters or from tabulated data. Use the Leakage and friction parameterization parameter to select the exact input type.Input efficiencies— Provide the mechanical and volumetric efficiencies directly through physical signal input ports.Input losses— Provide the mechanical and volumetric losses directly through physical signal input ports. The mechanical loss is defined as the internal friction torque. The volumetric loss is defined as the internal leakage flow rate.
Displacement Parameterizations
The displacement volume input depends on the block variant selected. If the active block
variant is Input efficiencies or Input
losses, the block obtains the instantaneous displacement volume directly
from the physical signal input at port D.
If the active block variant is Analytical or tabulated data,
the block computes the instantaneous displacement volume from the control member position
specified at port C. This computation depends on the Displacement
parameterization parameter setting:
Maximum displacement and control member stroke— Compute the displacement volume per unit rotation as a linear function of the control member position specified at port C.Displacement vs. control member position table— Compute the displacement volume per unit volume using interpolation or extrapolation of displacement tabular data specified at discrete control member positions.
Flow Rate and Driving Torque
The volumetric flow rate generated at the motor is
where:
q is the net volumetric flow rate.
qIdeal is the ideal volumetric flow rate.
qLeak is the internal leakage volumetric flow rate.
The torque generated at the motor is
where:
τ is the net torque.
τIdeal is the ideal torque.
τFriction is the friction torque.
The ideal volumetric flow rate is
and the ideal generated torque is
where:
DSat is a smoothed displacement computed so as to remove numerical discontinuities between negative and positive displacements.
ω is the instantaneous angular velocity of the rotary shaft.
Δp is the instantaneous pressure drop from inlet to outlet.
The saturation displacement depends on the block variant selected. If the active
variant is Analytical or tabulated data,
where:
D is the instantaneous fluid displacement determined from the physical signal input specified at port C or port D.
DMax is the specified value of the Maximum displacement block parameter.
DThreshold is the specified value of the Displacement threshold for motor-pump transition block parameter.
If the active variant is Input efficiencies or
Input losses, there is no upper bound on the displacement
input and the saturation displacement reduces to:
The internal leakage flow rate and friction torque calculations depend on the block
variant selected. If the block variant is Analytical or tabulated
data, the calculations depend also on the Leakage and friction
parameterization parameter setting. There are five possible permutations of
block variant and parameterization settings.
Case 1: Analytical Efficiency Calculation
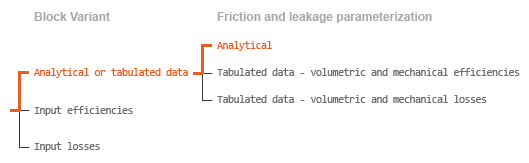
If the active block variant is Analytical or tabulated data
and the Leakage and friction parameterization parameter is set to
Analytical, the leakage flow rate is
and the friction torque is
where:
KHP is the Hagen-Poiseuille coefficient for laminar pipe flows. This coefficient is computed from the specified nominal parameters.
KTP is the specified value of the Friction torque vs pressure drop coefficient block parameter.
τ0 is the specified value of the No-load torque block parameter.
ωThreshold is the threshold angular velocity for the motor-pump transition. The threshold angular velocity is an internally set fraction of the specified value of the Nominal shaft angular velocity block parameter.
The Hagen-Poiseuille coefficient is determined from nominal fluid and component parameters through the equation
where:
νNom is the Nominal kinematic viscosity parameter. This is the kinematic viscosity at which the nominal volumetric efficiency is specified.
ρNom is the Nominal fluid density parameter. This is the density at which the nominal volumetric efficiency is specified.
ρ is the actual fluid density in the attached hydraulic (isothermal liquid) network. This density can differ from the Nominal fluid density parameter.
ωNom is the Nominal shaft angular velocity parameter. This is the angular velocity at which the nominal volumetric efficiency is specified.
v is the fluid kinematic viscosity in the attached hydraulic fluid network.
ΔpNom is the Nominal pressure drop parameter. This is the pressure drop at which the nominal volumetric efficiency is specified.
ηv,Nom is the Volumetric efficiency at nominal conditions parameter. This is the volumetric efficiency corresponding to the specified nominal conditions.
Case 2: Efficiency Tabulated Data
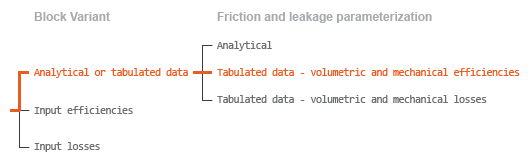
If the active block variant is Analytical or tabulated data
and the Leakage and friction parameterization parameter is set to
Tabulated data — volumetric and mechanical
efficiencies, the leakage flow rate is
and the friction torque is
where:
α is a numerical smoothing parameter for the motor-pump transition.
qLeak,Motor is the leakage flow rate in motor mode.
qLeak,Pump is the leakage flow rate in pump mode.
τFriction,Pump is the friction torque in pump mode.
τFriction,Motor is the friction torque in motor mode.
The smoothing parameter α is given by the hyperbolic function
where:
ΔpThreshold is the specified value of the Pressure drop threshold for motor-pump transition block parameter.
ωThreshold is the specified value of the Angular velocity threshold for motor-pump transition block parameter.
DThreshold is the specified value of the Displacement threshold for motor-pump transition block parameter.
The leakage flow rate is computed from efficiency tabulated data through the equation
in motor mode and through the equation
in pump mode, where:
ηv is the volumetric efficiency obtained through interpolation or extrapolation of the Volumetric efficiency table, e_v(dp,w,D) parameter data.
Similarly, the friction torque is computed from efficiency tabulated data through the equation
in motor mode and through the equation
in pump mode, where:
ηm is the mechanical efficiency obtained through interpolation or extrapolation of the Mechanical efficiency table, e_m(dp,w,D) parameter data.
Case 3: Loss Tabulated Data
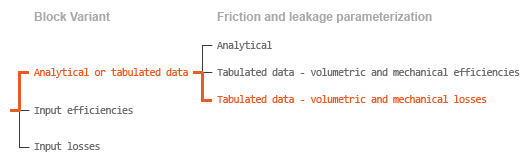
Analytical or tabulated
data and the Leakage and friction parameterization
parameter is set to Tabulated data — volumetric and mechanical
losses, the leakage flow rate equation is
and the friction torque equation is
where qLeak(Δp,ω,DSat) and τFriction(Δp,ω,DSat) are the volumetric and mechanical losses, obtained through interpolation or extrapolation of the Volumetric loss table, q_loss(dp,w) and Mechanical loss table, torque_loss (dp,w) parameter data.
Case 4: Efficiency Physical Signal Inputs
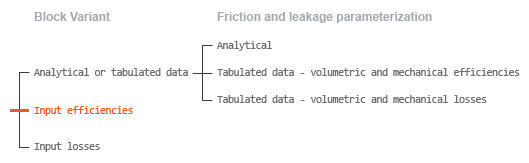
If the active block variant is Input efficiencies, the
leakage flow rate and friction torque calculations are as described for efficiency
tabulated data (case 2). The volumetric and mechanical efficiency lookup tables are
replaced with physical signal inputs that you specify through ports EV and EM.
Case 5: Loss Physical Signal Inputs
If the block variant is Input losses, the leakage flow rate
and friction torque calculations are as described for loss tabulated data (case 3). The
volumetric and mechanical loss lookup tables are replaced with physical signal inputs that
you specify through ports LV and LM.
Assumptions
Fluid compressibility is negligible.
Loading on the motor shaft due to inertia, friction, and spring forces is negligible.

