bfsearch
Breadth-first graph search
Syntax
Description
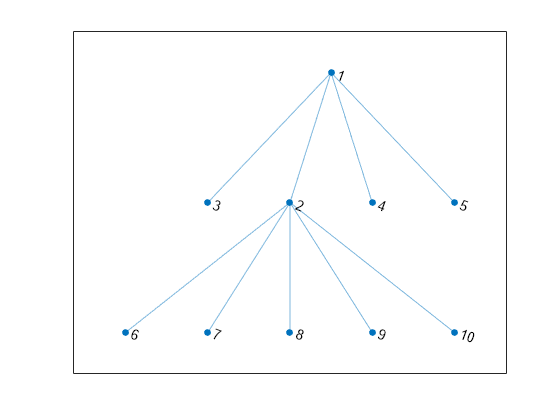
v = bfsearch(G,s)G starting at node s. The result is a vector of
node IDs in order of their discovery.
[___] = bfsearch(___,'Restart',,
where tf)tf is true, restarts the search if no new
nodes are reachable from the discovered nodes. You can use any of the input or output
argument combinations in previous syntaxes. This option ensures that the breadth-first
search reaches all nodes and edges in the graph, even if they are not reachable from the
starting node, s.
Examples
Input Arguments
Output Arguments
Tips
dfsearchandbfsearchtreat undirected graphs the same as directed graphs. An undirected edge between nodessandtis treated like two directed edges, one fromstotand one fromttos.
Algorithms
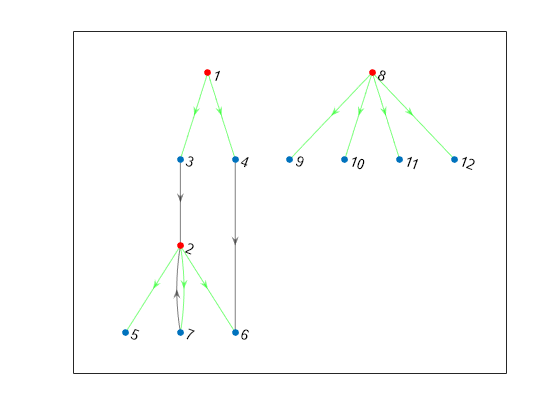
The Breadth-First search algorithm begins at the starting node, s, and
inspects all of its neighboring nodes in order of their node index. Then for each of those
neighbors, it visits their unvisited neighbors in order. The algorithm continues until all
nodes that are reachable from the starting node have been visited.
In pseudo-code, the algorithm can be written as:
Event startnode(S)
Event discovernode(S)
NodeList = {S}
WHILE NodeList is not empty
C = NodeList{1}
Remove first element from NodeList
FOR edge E from outgoing edges of node C, connecting to node N
Event edgetonew(C,E), edgetodiscovered(C,E) or edgetofinished(C,E)
(depending on the state of node N)
IF event was edgetonew
Event discovernode(N)
Append N to the end of NodeList
END
END
Event finishnode(C)
END
bfsearch can return flags to describe the different events in the
algorithm, such as when a new node is discovered or when all of the outgoing edges of a node
have been visited. The event flags are listed here.
| Event Flag | Event Description |
|---|---|
'discovernode' |
A new node has been discovered. |
'finishnode' |
All outgoing edges from the node have been visited. |
'startnode' |
This flag indicates the starting node in the search. |
'edgetonew' |
Edge connects to an undiscovered node |
'edgetodiscovered' |
Edge connects to a previously discovered node |
'edgetofinished' |
Edge connects to a finished node |
For more information, see the input argument description for
events.
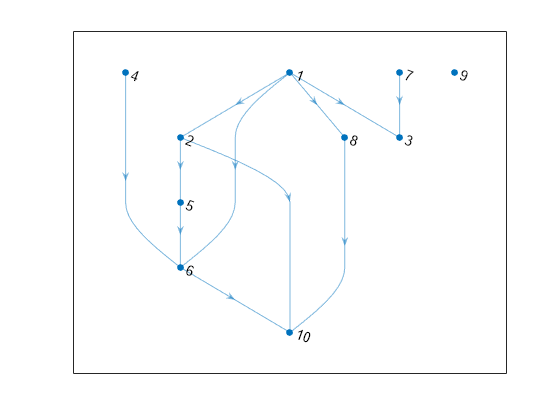
Note
In cases where the input graph contains nodes that are unreachable from the starting
node, the 'Restart' option provides a way to make the search visit every
node in the graph. In that case, the 'startnode' event indicates the
starting node each time the search restarts.
Extended Capabilities
Version History
Introduced in R2015b