Heat Transfer in a Thermal Liquid Pipe
This example shows how changes in mass flow rate, environment, and flow direction impact heat transfer in a pipe. These factors are important when designing cooling systems or heat exchangers. This example uses the Simscape™ Fluids™ Pipe (TL) block. For more information on pressure loss and flow rate in a pipe, see Pressure Loss and Mass Flow Rate in a Thermal Liquid Pipe.
Convective and Conductive Heat Transfer to the Environment
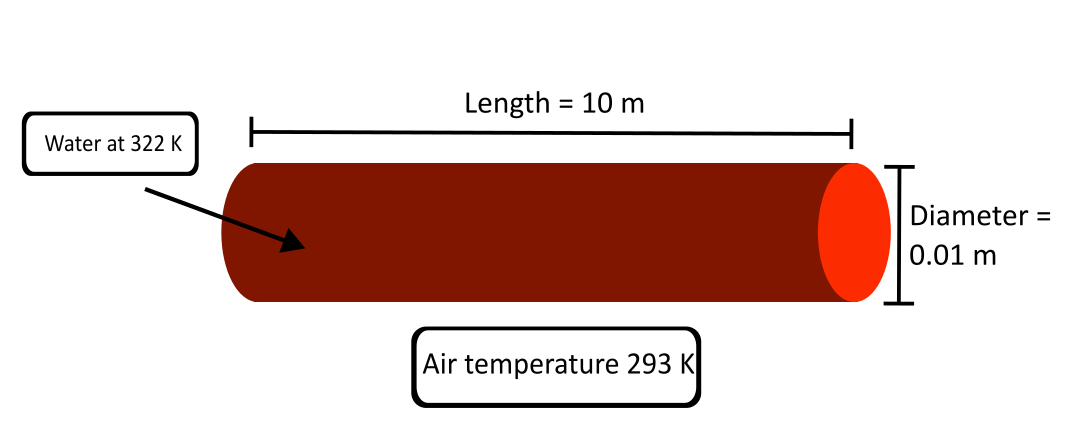
Consider a pipe that is 10 meters long with a circular cross-section and a 0.01 meter diameter. The temperature of the water in the pipe and the water that flows into the pipe is 322 K and the temperature of the air surrounding the pipe is 293 K. The mass flow rate through the pipe is 0.1 kg/s. The pipe wall is 0.005 m thick. You can use this information to calculate the heat transfer between the pipe and the environment while accounting for the convection between the outside pipe wall and the outside air.
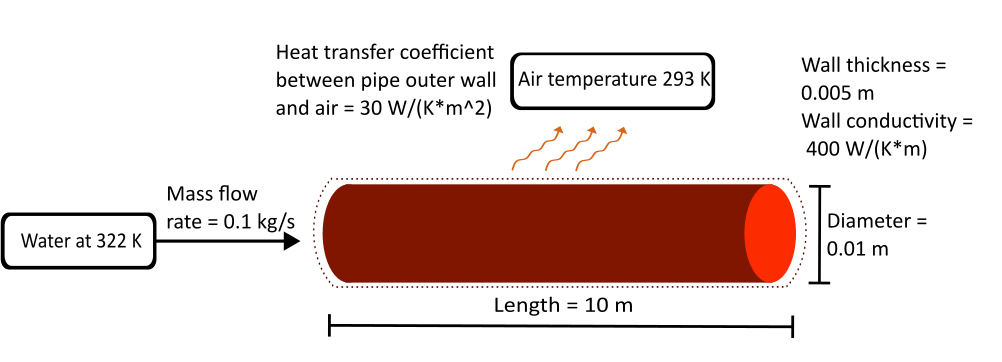
Create MATLAB® parameters to represent the pipe length, pipe diameter, water properties, and air temperature.
D = 0.01; % [m] Pipe diameter L = 10; % [m] Pipe length k = 0.614; % [W/(m*K)] Thermal conductivity of water T_I = 322; % [K] Initial temperature in pipe T_W = 293; % [K] Temperature of air surrounding pipe. This is also the temperature of the pipe wall c = 4181; % [J/(kg*K)] Water specific heat rho = 998; % [kg/m^3] Density of water
Calculate the surface area of the pipe walls and the mass of the water in the pipe.
mass = rho*L*pi*(D/2)^2; % [kg] Water mass in pipe S = pi*D*L; % [m^2] Surface area of pipe
The net heat transfer between the water and the outside air depends on the thermal resistances of the water, the pipe wall, and the convection with the outside air,
![]()
where ![]() is the temperature difference between the water and the outside air.
is the temperature difference between the water and the outside air. ![]() is the sum of the thermal resistances,
is the sum of the thermal resistances,
where the subscripts L, W, and A represent the liquid, wall, and air, respectively. The thermal resistances for water and air are
![]()
![]()
where:
is the thermal conductivity of the pipe wall.
is the heat transfer coefficient between the pipe outer wall and the air.
S is the surface area.
 is the pipe length.
is the pipe length.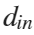 and
and 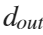 are the pipe inner and outer diameters, respectively.
are the pipe inner and outer diameters, respectively.
Create MATLAB parameters to represent the outer diameter of the pipe, thermal conductivity of the pipe wall, heat transfer coefficient with the outside air, and mass flow rate.
h_A = 30; % [W/(K*m^2)] Heat transfer coefficient between pipe outer wall and air k_W = 400; % [W/(K*m)] Thermal conductivity of pipe wall thick = 0.005; % [m] Pipe wall thickness D_out = D + 2*thick; % [m] Outer diameter of the pipe mdot = 0.1; % [kg/sec] Mass flow rate through pipe
If you assume that the pipe wall has a constant temperature along the entire length and that the pipe flow is thermally fully developed, then the difference between the fluid mean temperature and pipe wall temperature follows an exponential distribution along the pipe length. A pipe flow is thermally fully developed if the flow characteristics, such as the velocity or temperature profile, do not change along the length. The effective thermal resistance between the fluid and pipe for the entire pipe length is
where ![]() is the mass flow rate and is the heat transfer coefficient for flow within pipe, where is the Nusselt number.
is the mass flow rate and is the heat transfer coefficient for flow within pipe, where is the Nusselt number.
Calculate the Nusselt number in a turbulent flow using the Dittus-Boelter correlation,
![]()
where Re is the Reynolds number and Pr is the Prandtl number. Calculate the Nusselt number.
Pr = 7.35; % Prandtl number area = pi/4*D^2; % [m^2] Pipe cross-sectional area mu = 0.00108; % [Pa*s] Dynamic viscosity of water Re = mdot*D/(area*mu); % Reynolds number Nu = 0.023*Re^0.8*Pr^0.4; % Nusselt number
Use the Nusselt number to calculate the heat transfer coefficient for the flow in the pipe.
h_L = Nu*k/D; % [W/(m^2*K)] Heat transfer coefficient for flow within pipeUse the calculated value of ![]() to solve for the net heat transfer over the pipe, pipe wall, and convection with the outside air.
to solve for the net heat transfer over the pipe, pipe wall, and convection with the outside air.
R_L = 1/(c*mdot*(1-exp((-h_L*S)/(c*mdot)))); % [K/W] Thermal resistance due to liquid within the pipe R_W = log(D_out/D)/(2*pi*L*k_W); % [K/W] Thermal resistance due to the pipe wall R_A = 1/(h_A*L*D_out*pi); % [K/W] Thermal resistance due to convection with the outside air Q = (T_W-T_I)/(R_L+R_W+R_A) % [W] Net heat transfer over the pipe, pipe wall, and convection with the outside air
Q = -522.4732
Use the HeatTransferInPipeFlowSource model to confirm the calculated value for net heat transfer. The model settings and parameters match the conditions described above.

Run the model and plot the heat transfer and temperature in the pipe.
mdl = 'HeatTransferInPipeFlowSource'; open_system(mdl); out = sim(mdl); t_model = out; % [sec] Model time Q_H = simlog_HeatTransferInPipeFlowSource.Pipe_TL.segment.Q_H.series.values; % [kW] Model heat transfer temp_flow = simlog_HeatTransferInPipeFlowSource.Pipe_TL.segment.T_I.series.values; % [K] Model pipe temperature figure plot(t_model,Q_H*1000) xlabel('Time (s)') ylabel('Heat Transfer Rate (W)')
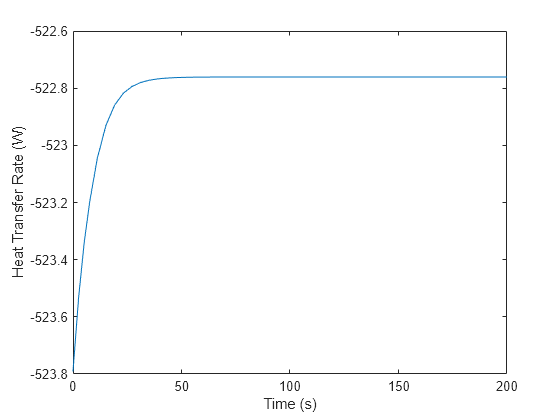
figure plot(t_model,temp_flow) xlabel('Time (s)') ylabel('Temperature (K)')
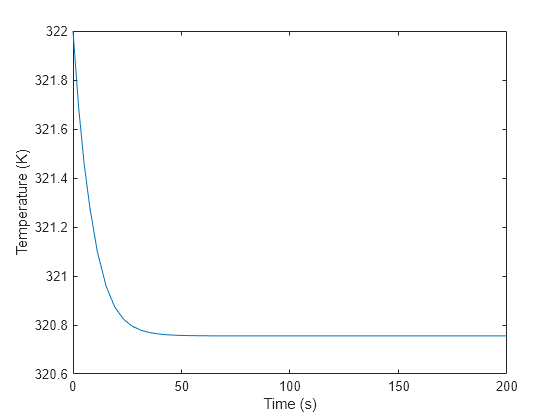
The model steady state heat transfer is about -522.8 W, which agrees with the analytical results. Because the model uses more precise values for fluid attributes and accounts for dynamics, the generated values are slightly different. The steady state temperature in the pipe is about 320.8 K. This is only about 1 K less than the initial temperature and demonstrates that this is not an effective physical scenario for cooling the water in the pipe.
Heat Transfer Between Two Pipes
Suppose that the pipe in the previous section is now surrounded by a larger outer pipe that has a diameter of 0.2 m. Water flows through the outer pipe at the same mass flow rate, but the enters the pipe at 293 K and exits at 307.3 K. Water exits the inner pipe at 307.5 K. Because the outer wall is perfectly insulated, you can ignore the effects of the wall between the two pipes and the outside environment. Initially, the flow is parallel from left to right for both tubes. This scenario represents the simplest version of a shell and tube parallel-flow heat exchanger.
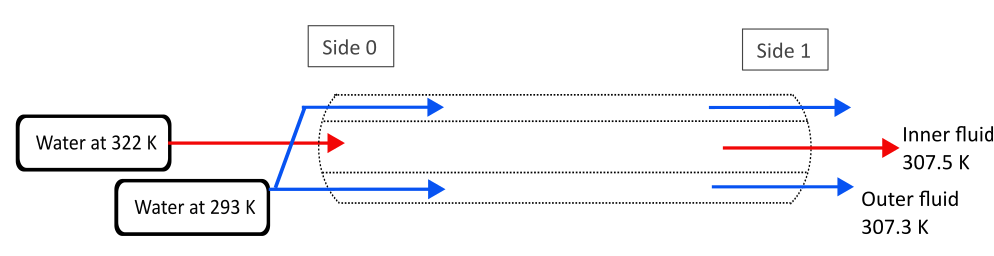
The heat transfer between the pipes is
![]()
where ![]() is the temperature difference between the two pipes on the left side, and
is the temperature difference between the two pipes on the left side, and ![]() is the temperature difference between the pipes on the right side. Assume that
is the temperature difference between the pipes on the right side. Assume that ![]() is the heat transfer coefficient for both pipes. This assumption and the equation for ignores the effect of heat transfer along the outer wall of the outside pipe. Solve for the heat transfer between the two pipes.
is the heat transfer coefficient for both pipes. This assumption and the equation for ignores the effect of heat transfer along the outer wall of the outside pipe. Solve for the heat transfer between the two pipes.
delT_0 = T_I-T_W; % [K] Temperature difference on the left side of the pipe delT_1 = 307.5-307.3; % [K] Temperature difference on the right side of the pipe Q = 1/(2/h_L)*S*(delT_0-delT_1)/log(delT_0/delT_1) % [W] Heat transfer between the pipes
Q = 5.1543e+03
Using a heat exchanger increases the rate of heat transfer, and the two fluid temperatures almost become equal over the length of the pipes.
Compare this solution to the HeatTransferInTwoTLPipes model, which matches these conditions. The Pipe (TL) block uses a lumped parameter model, which means it only models heat transfer at one point and does not model temperature changes along its length. To discretize the temperature model along the length of both pipes, the model divides the pipe into 5 pipe segments, each with length ![]() . For physical scenarios where the changes along the pipe are more dynamic, or for very long pipes, you may need to use more segments. However, for the steady state calculations here, five segments is sufficient.
. For physical scenarios where the changes along the pipe are more dynamic, or for very long pipes, you may need to use more segments. However, for the steady state calculations here, five segments is sufficient.
n_seg=5; % Number of pipe segments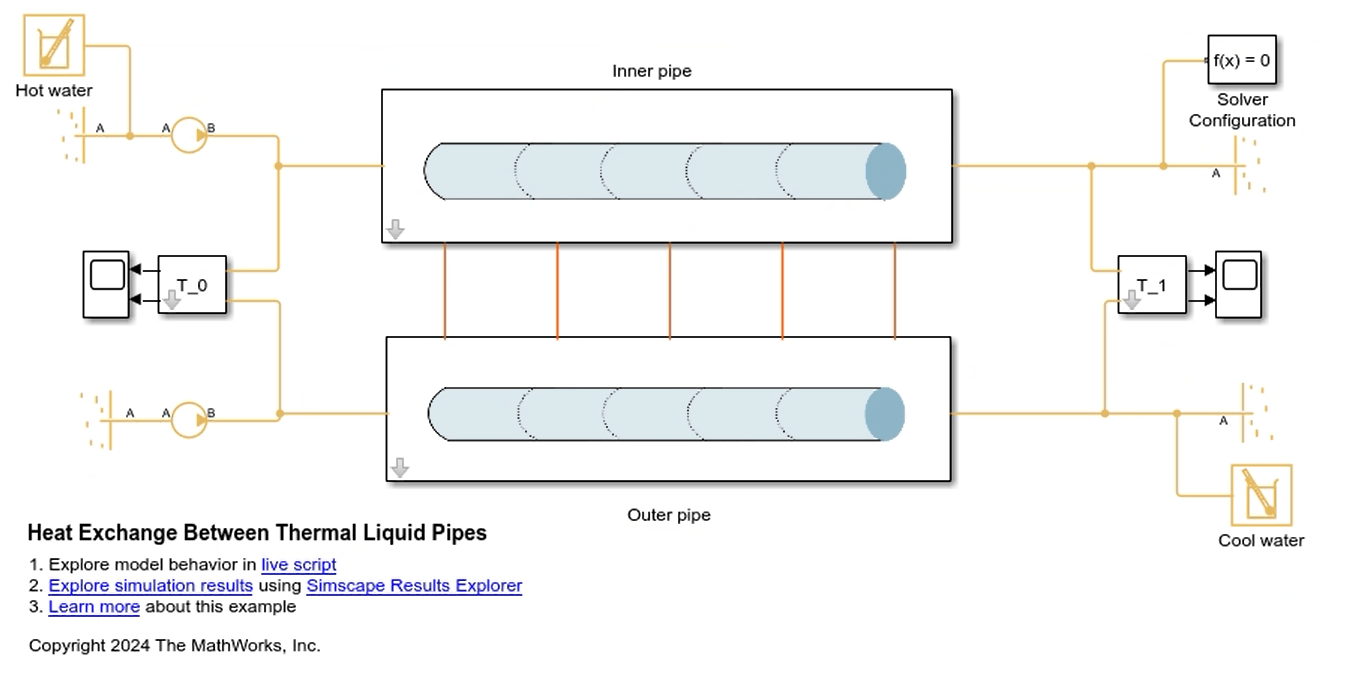
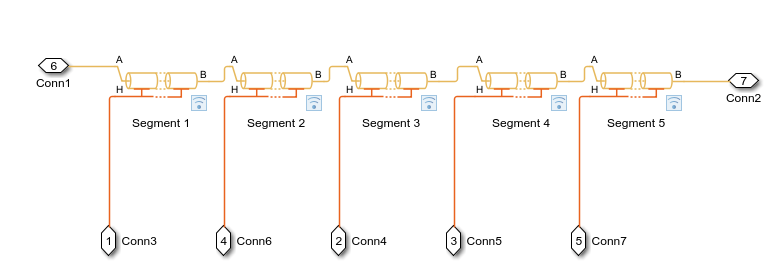
Inside the Inner pipe and Outer pipe subsystems are five Pipe (TL) blocks connected in series.
Simulate the model to confirm the calculated value heat transfer rate between the two pipes.
mdl = 'HeatTransferInTwoTLPipes'; open_system(mdl); out = sim(mdl); Q_1 = log_HeatTransfer.Outer_pipe.Segment_1.segment.Q_H.series.values*1000; % [W] Segment 1 heat transfer Q_2 = log_HeatTransfer.Outer_pipe.Segment_2.segment.Q_H.series.values*1000; % [W] Segment 2 heat transfer Q_3 = log_HeatTransfer.Outer_pipe.Segment_3.segment.Q_H.series.values*1000; % [W] Segment 3 heat transfer Q_4 = log_HeatTransfer.Outer_pipe.Segment_4.segment.Q_H.series.values*1000; % [W] Segment 4 heat transfer Q_5 = log_HeatTransfer.Outer_pipe.Segment_5.segment.Q_H.series.values*1000; % [W] Segment 5 heat transfer
Plot the heat transfer rate for each segment along the pipe and sum over the heat transfer rate for each segment.
plot(L/n_seg*[.5 1.5 2.5 3.5 4.5],[Q_1(end),Q_2(end),Q_3(end),Q_4(end),Q_5(end)],'.','MarkerSize',15) xlim([0 L]) ylim([0 4000]) xlabel('Length (m)') ylabel('Heat Transfer Rate (W)')
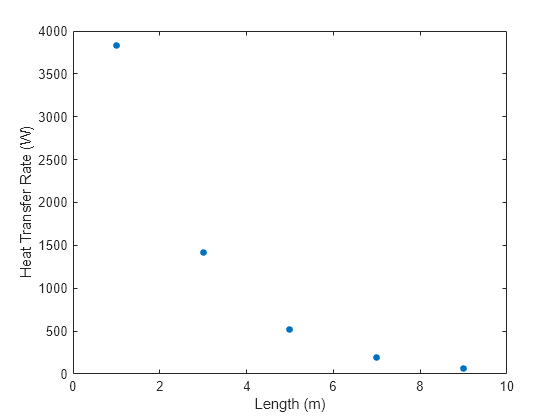
Q_model = Q_1(end)+Q_2(end)+Q_3(end)+Q_4(end)+Q_5(end) % [W] Heat transfer rate over the length of the pipeQ_model = 6.0231e+03
The simulated average heat transfer rate between the pipes is about 868 W higher than the analytical value, which is a 14% difference. This difference is partially because the Simscape model uses different values for fluid properties. Additionally, the Simscape block includes conductive heat transfer, which the analytical solution does not. In most pipe flow heat transfer scenarios, the conductive heat transfer is negligible compared to convective heat transfer.
The heat transfer rate drops in each segment along the direction of the flow of the water as the temperature difference between the two pipes decreases. This design is not effective for a heat exchanger because the rate of heat transfer is directly proportional to the temperature difference, and the majority of the heat transfer happens in the first segment and decreases exponentially in the remaining segments.
You can increase the efficiency of the model by replacing the parallel-flow heat exchanger with a counter-flow heat exchanger. In a counter-flow heat exchanger, where the liquids flow in opposite directions, the temperature difference along the length of the pipes is more constant, and the heat exchanger is more effective. Calculate the length of both pipes in a counter-flow heat exchanger for it to have the same efficiency as the parallel-flow case calculated above, is the rest of the conditions stay the same.

Rearrange the expression for the heat transfer between the pipes to solve for the necessary length of a counter-flow heat exchanger
![]()
Recalculate ![]() and
and ![]() to account for the changes in the water at both ends of the pipes then solve for length of the equivalent counter-flow heat exchanger.
to account for the changes in the water at both ends of the pipes then solve for length of the equivalent counter-flow heat exchanger.
delT_0 = T_I-307.3; % [K] Temperature difference on the left side of the pipe delT_1 = 307.5-T_W; % [K] Temperature difference on the left side of the pipe pipe_length = Q*(2/h_L)/(pi*D)*log(delT_0/delT_1)/(delT_0-delT_1) % [m] Length of equivalent counter-flow heat exchanger
pipe_length = 3.9637
The counter-flow heat exchanger is much more efficient, and only needs to be about a third as long to be as effective.
You can model a counter-flow heat exchanger with the HeatTransferInTwoTLPipes model. Set the mass flow rate through the outer pipe as negative. In this scenario, the water flows the opposite direction through the pipe. Set the length of both pipes to the length you calculated above.
mdl = 'HeatTransferInTwoTLPipes'; open_system(mdl); set_param('HeatTransferInTwoTLPipes/Flow Rate Source (TL)1','mass_flow','-mdot') L = pipe_length; out = sim(mdl); Q_1 = log_HeatTransfer.Outer_pipe.Segment_1.segment.Q_H.series.values*1000; % [W] Segment 1 heat transfer Q_2 = log_HeatTransfer.Outer_pipe.Segment_2.segment.Q_H.series.values*1000; % [W] Segment 2 heat transfer Q_3 = log_HeatTransfer.Outer_pipe.Segment_3.segment.Q_H.series.values*1000; % [W] Segment 3 heat transfer Q_4 = log_HeatTransfer.Outer_pipe.Segment_4.segment.Q_H.series.values*1000; % [W] Segment 4 heat transfer Q_5 = log_HeatTransfer.Outer_pipe.Segment_5.segment.Q_H.series.values*1000; % [W] Segment 5 heat transfer
Plot the rate of heat transfer in each segment.
plot(L/n_seg*[.5 1.5 2.5 3.5 4.5],[Q_1(end),Q_2(end),Q_3(end),Q_4(end),Q_5(end)],'.','MarkerSize',15) xlim([0 L]) ylim([0 4000]) xlabel('Time (s)') xlabel('Length (m)')
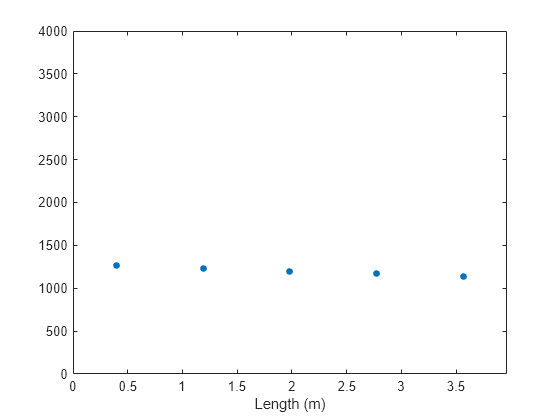
Q_model = Q_1(end)+Q_2(end)+Q_3(end)+Q_4(end)+Q_5(end) % [W] Heat transfer rate over the length of the pipeQ_model = 6.0042e+03
Because the temperature difference between the flows is more consistent along the length of the pipe, the rate of heat transfer in each segment is less varied and around 1200 W for each segment. The heat exchanger is more effective because each section of the pipe contributes more to the overall heat transfer rate, which is why the shorter heat exchanger can accomplish the same amount of cooling.
Conductive Heat Transfer
Suppose the same pipe as before has no mass flow rate. Because the pipe is thin, the wall temperature is constant, the pipe is sealed, and the flow is zero, any fluid motion driven by temperature difference in the pipe is negligible, so you can ignore the effect of convective heat transfer. Assume that the wall of the pipe is arbitrarily thin and does not impact the heat transfer through it. You can use this information to calculate the conductive heat transfer that acts from the center of the pipe outwards through the side walls.
The conductive heat transfer through a cylindrical pipe is
where:
k is the thermal conductivity of water.
L is the pipe length.
D is the pipe diameter.
is the temperature at the pipe wall.
T is the temperature of the water in the pipe.
is the inner diameter in the pipe where the temperature is T. If you model conduction through a pipe wall, is the inner diameter of the pipe. For this example, assume that to approximate the behavior of the Simscape block, which uses a lumped parameter model for the water in the pipe that assumes that the water has a constant temperature profile.
L = 10; % [m] Pipe length Q_cond = 2*pi*L*k*(T_W-T_I)/log(D/(.13*D)) % [W] Conductive heat transfer
Q_cond = -548.3642
The conductive heat transfer is an order of magnitude smaller than the convective heat transfer that you previously calculated. Conductive heat transfer contributes less to overall heat transfer than convective heat transfer in most pipe flows.
You can use the expression for conduction to solve for a closed form solution for the temperature of the water in the pipe. If you treat the pipe as lumped parameter model with a uniform internal temperature,
where:
U is the total internal energy.
is the specific heat.
m is the mass.
 is time.
is time.
The first rule of thermodynamics states that ![]() . Use this relation to express the heat transfer in the pipe in terms of the temperature derivative,
. Use this relation to express the heat transfer in the pipe in terms of the temperature derivative,
This equation is a first order differential equation with the solution where
Use a Simscape model to confirm the analytical results. Open the HeatTransferInPipeConductive model.

mdl = 'HeatTransferInPipeConductive';
open_system(mdl);
out = sim(mdl);Calculate the analytical solution, then plot the simulation results and compare the model and analytical solutions.
t = 0:.5:1000; % [sec] Time for analytical solution T = T_W + (T_I-T_W) .*exp(-t.*((2*k*pi*L)/(log(D/(0.13*D))*c*mass))); % [K] Temperature analytical solution t_model = out; % [sec] Model time temperature_model = simlog_ConductiveHeatTransferInPipe.Pipe_TL.segment.T_I.series.values; % [K] Model temperature figure plot(t,T,t_model,temperature_model) xlabel('Time (s)') ylabel('Temperature (K)') legend('Analytical Solution','Model Results')
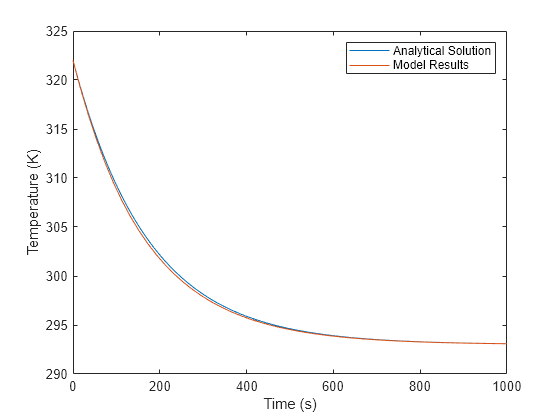
The model results and the analytical solution closely agree. Because there are no additional sources of heat, the temperature in the pipe approaches the air temperature. However, because the heat transfer from convection is smaller, it takes significantly more time to reach cooler temperatures than in the previous models where there is convection.
References
[1] Adrienne S. Lavine, Frank P. Incropera, David P. DeWitt, Theodore L. Bergman. Fundamentals of heat and mass transfer. Vol. 6. New York: Wiley, 1996.