Lateral Driver
Lateral path-tracking controller
Libraries:
Vehicle Dynamics Blockset /
Vehicle Scenarios /
Driver
Description
The Lateral Driver block implements a control model to generate normalized steering commands that track a lateral reference displacement. The normalized steering commands can vary between -1 to 1. To model the dynamics, the block uses a linear single track (bicycle) model. Use the Lateral Driver block to:
Close the loop between a predefined path and actual vehicle motion.
Generate steering commands that track predefined paths. You can connect the Lateral Driver block output to steering block inputs.
Configurations
Use the External Actions parameters to create input ports for signals that can disable, hold, or override the closed-loop steering command. The block uses this priority order for the input commands: disable (highest), hold, override. The block uses this priority order for the input commands: disable (highest), hold, override.
This table summarizes the external action parameters.
| Goal | External Action Parameter | Input Ports | Data Type |
|---|---|---|---|
Override the steering command with an input steering command. | Steering override |
| Boolean |
| double | ||
Hold the steering command at the current value. | Steering hold | SteerHld | Boolean |
Disable the steering command. | Steering disable | SteerZero | Boolean |
Use the Output handwheel angle parameter to specify the units for the steering ports.
Setting | Block Implementation | Port | |
|---|---|---|---|
| Commanded steer angle, normalized from -1 through 1. The block uses the tire wheel angle saturation limit Tire wheel angle limit, theta parameter to normalize the command. |
| |
Overrides the steering command with an input steering command normalized from -1 through 1. |
| ||
| Commanded steer angle, in units specified by Angular units, angUnits. |
| |
Overrides the steering command with an input steering command, in units specified by Angular units, angUnits. |
| ||
Also, you can specify a tire wheel angle saturation limit using the Tire wheel angle limit, theta parameter.
Use the Lateral control type, controlTypeLat parameter to specify the type of lateral control. The table specifies the block implementation.
Setting | Block Implementation | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Optimal single-point preview (look ahead) control model developed by C. C. MacAdam1, 2, 3. The model represents driver steering control behavior during path-following and obstacle avoidance maneuvers. Drivers preview (look ahead) to follow a predefined path. | ||||||||||||
| Controller that uses the Stanley4 method to minimize the position error and the angle error of the current pose with respect to the reference pose. On the Reference Control pane, use the:
|
Use the Angular units, angUnits parameter to specify the angular units for the input and output ports.
Controller: Predictive Lateral Path-Tracking
If you set Lateral control type, controlTypeLat to
Predictive, the Lateral Driver block
implements an optimal single-point preview (look ahead) control model developed by C. C.
MacAdam1, 2, 3. The model represents driver steering control
behavior during path-following and obstacle avoidance maneuvers. Drivers preview (look
ahead) to follow a predefined path. To implement the MacAdam model, the block:
Represents the dynamics as a linear single track (bicycle) vehicle
Minimizes the previewed error signal at a single point T* seconds ahead in time
Accounts for the driver lag deriving from perceptual and neuromuscular mechanisms
This figure illustrates the block implementation of the single-point version of the driver model.
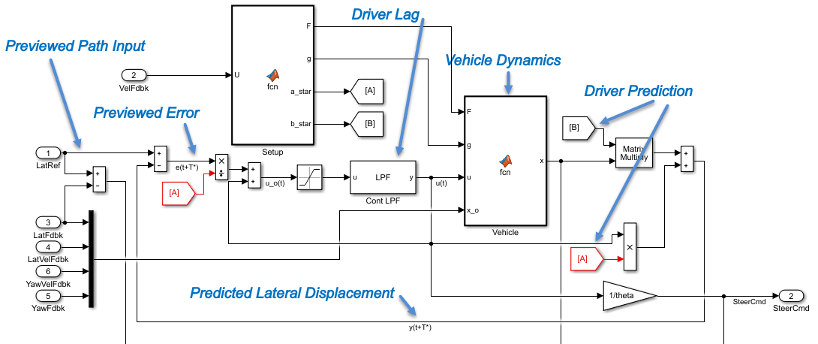
For lateral and yaw motion, the block implements these linear dynamic equations.
In matrix notation:
The single-point model assumes a minimum previewed error signal at a single point T* seconds ahead in time. a* is the driver ability to predict the future vehicle response based on the current steering control input. b* is the driver ability to predict the future vehicle response based on the current vehicle state. The block uses these equations.
The equations use these variables.
| a, b |
Forward and rearward tire location, respectively |
| m |
Vehicle mass |
| I |
Vehicle rotational inertia |
| CɑF |
Front tire cornering coefficient |
| CɑR |
Rear tire cornering coefficient |
| a*, b* |
Driver prediction scalar and vector gain, respectively |
| x |
Predicted vehicle state vector |
| v | Lateral velocity |
| r |
Yaw rate |
| Ψ |
Front wheel heading angle |
| y |
Lateral displacement |
| F |
System matrix |
| δ, δF | Steer angle and front axle steer angle, respectively |
| g |
Control coefficient vector |
| U | Forward (longitudinal) vehicle velocity |
| T* |
Preview time window |
| ƒ(t+T*) |
Previewed path input T* seconds ahead |
| U |
Forward vehicle velocity |
| mT |
Constant observer vector; provides vehicle lateral position |
The single-point model implemented by the block finds the steering command that minimizes a local performance index, J, over the current preview interval, (t, t+T).
To minimize J with respect to the steering command, this condition must be met.
You can express the optimal control solution in terms of a current non-optimal and corresponding nonzero preview output error T* seconds ahead1, 2, 3.
The block uses the preview distance and vehicle longitudinal velocity to determine the preview time window.
The equations use these variables.
| T* | Preview time window |
| ƒ(t+T*) | Previewed path input T* sec ahead |
| y(t+T*) | Previewed plant output T* sec ahead |
| e(t+T*) | Previewed error signal T* sec ahead |
| u(t), uo(t) | Steer angle and optimal steer angle, respectively |
| L | Preview distance |
| J | Performance index |
| U | Forward (longitudinal) vehicle velocity |
The single-point model implemented by the block introduces a driver lag. The driver lag accounts for the delay when the driver is tracking tasks. Specifically, it is the transport delay deriving from perceptual and neuromuscular mechanisms. To calculate the driver transport delay, the block implements this equation.
The equations use these variables.
| τ | Driver transport delay |
| y(t+T*) | Previewed plant output T* sec ahead |
| e(t+T*) | Previewed error signal T* sec ahead |
| u(t), uo(t) | Steer angle and optimal steer angle, respectively |
| J | Performance index |
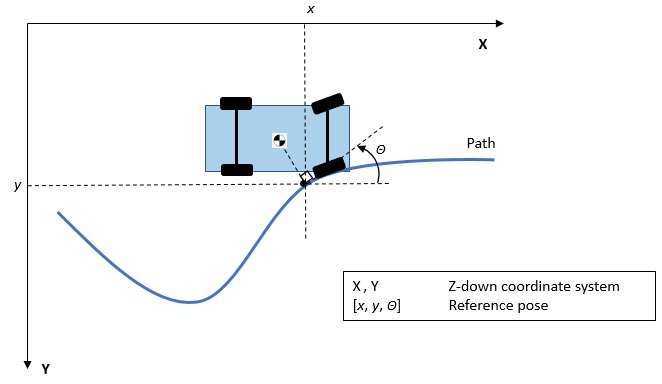
Controller: Stanley Lateral Path-Tracking
If you set Lateral control type, controlTypeLat to
Stanley, the block implements the Stanley
method4. To compute the steering angle command, the Stanley
controller minimizes the position error and the angle error of the current pose with respect
to the reference pose. The driving direction of the vehicle determines these error
values.
To compute the steering angle command, the controller minimizes the position error and the angle error of the current pose with respect to the reference pose.
The position error is the lateral distance from the vehicle center-of-gravity (CG) to the reference point on the path.
The angle error is the angle of the vehicle with respect to reference path.
Examples
Ports
Input
Output
Parameters
References
[1] MacAdam, C. C. "An Optimal Preview Control for Linear Systems". Journal of Dynamic Systems, Measurement, and Control. Vol. 102, Number 3, Sept. 1980.
[2] MacAdam, C. C. "Application of an Optimal Preview Control for Simulation of Closed-Loop Automobile Driving ". IEEE Transactions on Systems, Man, and Cybernetics. Vol. 11, Issue 6, June 1981.
[3] MacAdam, C. C. Development of Driver/Vehicle Steering Interaction Models for Dynamic Analysis. Final Technical Report UMTRI-88-53. Ann Arbor, Michigan: The University of Michigan Transportation Research Institute, Dec. 1988.
[4] Hoffmann, Gabriel M., Claire J. Tomlin, Michael Montemerlo, and Sebastian Thrun. "Autonomous Automobile Trajectory Tracking for Off-Road Driving: Controller Design, Experimental Validation and Racing." American Control Conference. 2007, pp. 2296–2301. doi:10.1109/ACC.2007.4282788
Extended Capabilities
Version History
Introduced in R2018a