isomorphism
Compute isomorphism between two graphs
Description
P = isomorphism(G1,G2)G1 and G2,
if one exists. If no isomorphism exists, then P is an empty
array.
P = isomorphism(___,Name,Value)'NodeVariables' and a list of node
variables to indicate that the isomorphism must preserve these variables to be
valid.
Examples
Compute Isomorphism Permutation
Create and plot two directed graphs, and then calculate the isomorphism relation between them.
G1 = digraph([1 1 1 2 3 4],[2 3 4 4 4 1]); G2 = digraph([3 3 3 2 1 4],[1 4 2 3 2 2]); subplot(1,2,1) plot(G1) subplot(1,2,2) plot(G2)

p = isomorphism(G1,G2)
p = 4×1
3
1
4
2
The result indicates that reordernodes(G2,p) has the same structure as G1.
Compute Isomorphism Between Graphs with Different Labels and Layouts
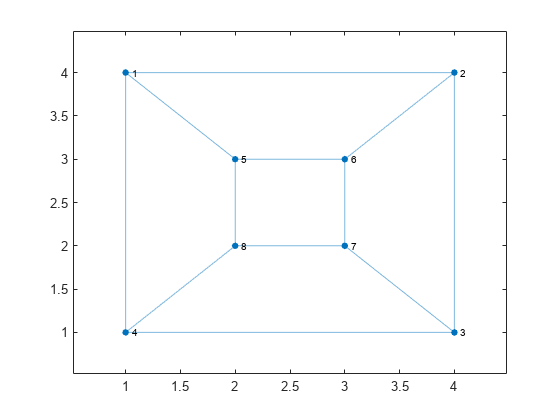
Create and plot two graphs, G1 and G2.
G1 = graph([1 1 1 2 2 3 3 4 5 5 7 7],[2 4 5 3 6 4 7 8 6 8 6 8]); plot(G1,'XData',[1 4 4 1 2 3 3 2],'YData',[4 4 1 1 3 3 2 2])
G2 = graph({'a' 'a' 'a' 'b' 'b' 'b' 'c' 'c' 'c' 'd' 'd' 'd'}, ...
{'g' 'h' 'i' 'g' 'h' 'j' 'g' 'i' 'j' 'h' 'i' 'j'});
plot(G2,'XData',[1 2 2 2 1 2 1 1],'YData',[4 4 3 2 3 1 2 1])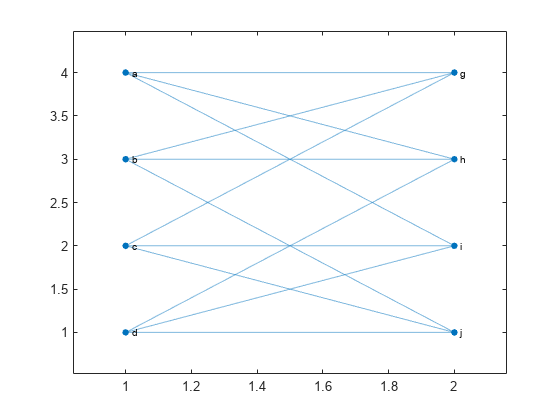
Compute the isomorphism relation between the graphs, if one exists. The result indicates that the graph nodes can be permuted to represent the same graph despite their different labels and layouts.
p = isomorphism(G1,G2)
p = 8×1
1
2
5
3
4
7
6
8
Compute Isomorphism and Preserve Node Properties
Compute two different isomorphism relations between two graphs. One of the relations preserves a node property, while the other ignores it.
Create two similar graphs. Add a node property Color to each of the graphs.
G1 = graph({'d' 'e' 'f'},{'e' 'f' 'd'});
G1.Nodes.Color = {'blue' 'red' 'red'}';
G2 = graph({'a' 'b' 'c'},{'b' 'c' 'a'});
G2.Nodes.Color = {'red' 'red' 'blue'}';Plot the graphs side-by-side in the same figure. Color the nodes red that have Color = 'red'.
subplot(1,2,1)
p1 = plot(G1);
highlight(p1,{'e' 'f'},'NodeColor','r')
subplot(1,2,2)
p2 = plot(G2);
highlight(p2,{'a' 'b'},'NodeColor','r')
Compute the isomorphism between the graphs, ignoring the Color property.
p = isomorphism(G1,G2)
p = 3×1
1
2
3
Compute the isomorphism again, but this time preserve the value of the Color property in the comparison. isomorphism returns a different permutation that preserves the Color property.
p = isomorphism(G1,G2,'NodeVariables','Color')
p = 3×1
3
1
2
View the nodes in G1 and G2 that the isomorphism matches together.
[G1.Nodes.Name, G2.Nodes.Name(p)]
ans = 3x2 cell
{'d'} {'c'}
{'e'} {'a'}
{'f'} {'b'}
Input Arguments
G1,G2 — Input graphs (as separate arguments)
graph objects | digraph objects
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: P = isomorphism(G1,G2,'NodeVariables',{'Var1'
'Var2'})
EdgeVariables — Edge variables to preserve
character vector | string scalar | cell array of character vectors | string array
Edge variables to preserve, specified as the comma-separated pair
consisting of 'EdgeVariables' and a character vector,
string scalar, cell array of character vectors, or string array. Use
this option to specify one or more edge variables that are in both
G1.Edges and G2.Edges. The
isomorphism must preserve the specified edge variables in order to be
valid.
If G is a multigraph, then you can specify the
second output edgeperms to enable reordering edge
variables.
Data Types: char | string | cell
NodeVariables — Node variables to preserve
character vector | string scalar | cell array of character vectors | string array
Node variables to preserve, specified as the comma-separated pair
consisting of 'NodeVariables' and a character vector,
string scalar, cell array of character vectors, or string array. Use
this option to specify one or more node variables that are in both
G1.Nodes and G2.Nodes. The
isomorphism must preserve the specified node variables in order to be
valid.
Data Types: char | string | cell
Output Arguments
P — Permutation vector for isomorphism
column vector | []
Permutation vector for isomorphism, returned as a column vector when an
isomorphism exists or as the empty array [] when an
isomorphism does not exist. If P is not empty, then
reordernodes(G2,P) has the same structure as
G1.
edgeperm — Edge permutation
column vector
Edge permutation, returned as a column vector. When working with
multigraphs, the edge permutation vector enables you to preserve edge
variables specified by the 'EdgeVariables' name-value
pair. Use these commands to reorder the edge variables of repeated
edges:
[p,edgeperm] = isomorphism(g1,g2,'EdgeVariables',edgevars); g2perm = reordernodes(g2, p); g2perm.Edges(:, 2:end) = g2perm.Edges(edgeperm, 2:end);
More About
Graph Isomorphism
Two graphs, G1 and G2, are
isomorphic if there exists a permutation of the nodes P such that
reordernodes(G2,P) has the same structure as
G1.
Two graphs that are isomorphic have similar structure. For example, if a graph contains one cycle, then all graphs isomorphic to that graph also contain one cycle.
Extended Capabilities
Thread-Based Environment
Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool.
Version History
Introduced in R2016b
Commande MATLAB
Vous avez cliqué sur un lien qui correspond à cette commande MATLAB :
Pour exécuter la commande, saisissez-la dans la fenêtre de commande de MATLAB. Les navigateurs web ne supportent pas les commandes MATLAB.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)