Specify GARCH Models
Default GARCH Model
The default GARCH(,) model in Econometrics Toolbox™ is of the form
,
with Gaussian innovation distribution and
.
The default model has no mean offset, and the lagged variances and squared innovations are at consecutive lags. For more details on GARCH models, see What Is a GARCH Model?
You can specify a model of this form using the shorthand syntax garch(P,Q). For the input arguments P and Q, enter the number of lagged conditional variances (GARCH terms), , and lagged squared innovations (ARCH terms), , respectively. The following restrictions apply:
and must be nonnegative integers.
If , the GARCH(,) model reduces to an ARCH() model.
If , you must also specify .
When you use this shorthand syntax, garch creates a garch model object with these default property values.
Property | Default Value |
|---|---|
| Number of GARCH terms |
| Number of ARCH terms |
|
|
|
|
| Cell vector of |
| Cell vector of |
|
|
To assign nondefault values to any properties, you can modify the created model using dot notation.
For example, use garch to create the GARCH(1,1) model
,
with Gaussian innovation distribution and
.
Mdl = garch(1,1)
Mdl =
garch with properties:
Description: "GARCH(1,1) Conditional Variance Model (Gaussian Distribution)"
SeriesName: "Y"
Distribution: Name = "Gaussian"
P: 1
Q: 1
Constant: NaN
GARCH: {NaN} at lag [1]
ARCH: {NaN} at lag [1]
Offset: 0
The returned model Mdl has NaNs for all model parameters. A NaN value signals to object functions, such as estimate, that a parameter needs to be estimated or otherwise specified by you. You must specify all parameters to, for example, forecast or simulate the model using forecast or simulate.
To estimate parameters, input the model and data to the estimate function. This function returns a fitted garch model object. The properties of the fitted model contain parameter estimates for the corresponding NaN values of the input model.
When you call garch without specifying input arguments, garch returns a GARCH(0,0) model object containing default property values. Inspect the default values of a default garch model object.
DefaultMdl = garch
DefaultMdl =
garch with properties:
Description: "GARCH(0,0) Conditional Variance Model (Gaussian Distribution)"
SeriesName: "Y"
Distribution: Name = "Gaussian"
P: 0
Q: 0
Constant: NaN
GARCH: {}
ARCH: {}
Offset: 0
Create GARCH Model By Using Shorthand Syntax
Use the shorthand garch(P,Q) syntax to create the GARCH(1,1) model
,
with Gaussian innovation distribution and
Mdl = garch(1,1)
Mdl =
garch with properties:
Description: "GARCH(1,1) Conditional Variance Model (Gaussian Distribution)"
SeriesName: "Y"
Distribution: Name = "Gaussian"
P: 1
Q: 1
Constant: NaN
GARCH: {NaN} at lag [1]
ARCH: {NaN} at lag [1]
Offset: 0
The output shows that the model Mdl has NaN values for these model parameters:
Constant— the conditional variance model constant termGARCH— the lag 1 GARCH coefficientARCH— the lag 1 ARCH coefficient
The default innovation model offset, specified by Offset, is 0.
You can modify the model by using dot notation or by passing it and data to the estimate function.
Using Name-Value Arguments
The most flexible way to specify GARCH models is using name-value arguments. You
do not need, nor are you able, to specify a value for every model property.
garch assigns default values to any properties you do not (or
cannot) specify.
The general GARCH(P,Q) model is of the form
where and
The innovation distribution can be Gaussian or Student’s t. The default distribution is Gaussian.
In order to estimate, forecast, or simulate a model, you must specify the
parametric form of the model (for example, which lags correspond to nonzero
coefficients, the innovation distribution) and any known parameter values. You can
set any unknown parameters equal to NaN, and then input the model
to estimate (along with data) to get estimated parameter values.
garch (and estimate) returns a model corresponding to the model specification. You can modify models to change or update the specification. Input models (with no NaN values) to forecast or simulate for forecasting and simulation, respectively. Here are some example specifications using name-value arguments.
| Model | Specification |
|---|---|
| garch('GARCH',NaN,'ARCH',NaN) or garch(1,1) |
| garch('Offset',NaN,'GARCH',NaN,'ARCH',NaN,... |
| garch('Constant',0.1,'GARCH',0.6,'ARCH',0.3,... |
Here is a full description of the name-value arguments you can use to specify GARCH models.
Note
You cannot assign values to the properties P and Q. garch sets these properties equal to the largest GARCH and ARCH lags, respectively.
Name-Value Arguments for GARCH Models
| Name | Corresponding GARCH Model Term(s) | When to Specify |
|---|---|---|
Offset | Mean offset, μ | To include a nonzero mean offset. For example, By default, |
Constant | Constant in the conditional variance model, κ | To set equality constraints for κ. For example, if a model has known constant 0.1, specify By default, |
GARCH | GARCH coefficients, | To set equality constraints for the GARCH coefficients. For example, to specify the GARCH coefficient in the model specify You only need to specify the nonzero elements of Any coefficients you specify must satisfy all stationarity and positivity constraints. |
GARCHLags | Lags corresponding to nonzero GARCH coefficients |
Use this argument as a shortcut for specifying specify Use |
ARCH | ARCH coefficients, | To set equality constraints for the ARCH coefficients. For example, to specify the ARCH coefficient in the model specify You only need to specify the nonzero elements of Any coefficients you specify must satisfy all stationarity and positivity constraints. |
ARCHLags | Lags corresponding to nonzero ARCH coefficients |
Use this argument as a shortcut for specifying specify Use |
Distribution | Distribution of the innovation process | Use this argument to specify a Student’s t innovation distribution. By default, the innovation distribution is Gaussian. For example, to specify a t distribution with unknown degrees of freedom, specify To specify a t innovation distribution with known degrees of freedom, assign |
Specify GARCH Model Using Econometric Modeler App
You can specify the lag structure and innovation distribution of GARCH models using the Econometric Modeler app. The app treats all coefficients as unknown and estimable, including the degrees of freedom parameter for a t innovation distribution.
At the command line, open the Econometric Modeler app.
econometricModeler
Alternatively, open the app from the apps gallery (see Econometric Modeler).
In the app, you can see all supported models by selecting a time series variable for the response in the Time Series pane. Then, on the Econometric Modeler tab, in the Models section, click the arrow to display the models gallery.
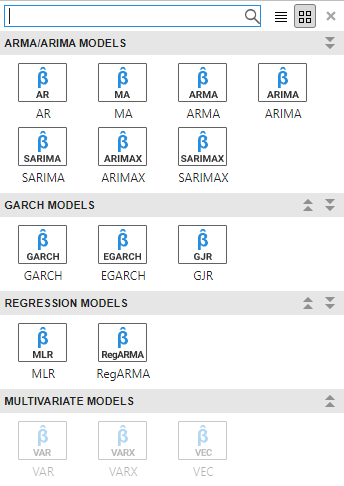
The GARCH Models section contains all supported conditional variance models. To specify a GARCH model, click GARCH. The GARCH Model Parameters dialog box appear.
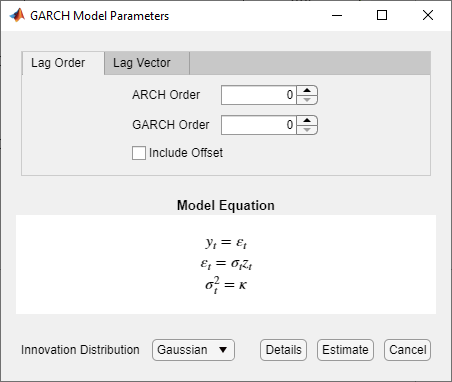
Adjustable parameters include:
GARCH Degree – The order of the GARCH polynomial
ARCH Degree – The order of the ARCH polynomial
Include Offset – The inclusion of a model offset
Innovation Distribution – The innovation distribution
As you adjust parameter values, the equation in the Model Equation section changes to match your specifications. Adjustable parameters correspond to input and name-value pair arguments described in the previous sections and in the garch reference page.
For more details on specifying models using the app, see Fitting Models to Data and Specifying Univariate Lag Operator Polynomials Interactively.
Specify GARCH Model with Mean Offset
This example shows how to specify a GARCH(P, Q) model with a mean offset. Use name-value pair arguments to specify a model that differs from the default model.
Specify a GARCH(1,1) model with a mean offset,
where and
Mdl = garch('Offset',NaN,'GARCHLags',1,'ARCHLags',1)
Mdl =
garch with properties:
Description: "GARCH(1,1) Conditional Variance Model with Offset (Gaussian Distribution)"
SeriesName: "Y"
Distribution: Name = "Gaussian"
P: 1
Q: 1
Constant: NaN
GARCH: {NaN} at lag [1]
ARCH: {NaN} at lag [1]
Offset: NaN
The mean offset appears in the output as an additional parameter to be estimated or otherwise specified.
Specify GARCH Model with Known Parameter Values
This example shows how to specify a GARCH model with known parameter values. You can use such a fully specified model as an input to simulate or forecast.
Specify the GARCH(1,1) model
with a Gaussian innovation distribution.
Mdl = garch('Constant',0.1,'GARCH',0.7,'ARCH',0.2)
Mdl =
garch with properties:
Description: "GARCH(1,1) Conditional Variance Model (Gaussian Distribution)"
SeriesName: "Y"
Distribution: Name = "Gaussian"
P: 1
Q: 1
Constant: 0.1
GARCH: {0.7} at lag [1]
ARCH: {0.2} at lag [1]
Offset: 0
Because all parameter values are specified, the created model has no NaN values. The functions simulate and forecast don't accept input models with NaN values.
Specify GARCH Model with t Innovation Distribution
This example shows how to specify a GARCH model with a Student's t innovation distribution.
Specify a GARCH(1,1) model with a mean offset,
where and
Assume follows a Student's t innovation distribution with eight degrees of freedom.
tdist = struct('Name','t','DoF',8); Mdl = garch('Offset',NaN,'GARCHLags',1,'ARCHLags',1,... 'Distribution',tdist)
Mdl =
garch with properties:
Description: "GARCH(1,1) Conditional Variance Model with Offset (t Distribution)"
SeriesName: "Y"
Distribution: Name = "t", DoF = 8
P: 1
Q: 1
Constant: NaN
GARCH: {NaN} at lag [1]
ARCH: {NaN} at lag [1]
Offset: NaN
The value of Distribution is a struct array with field Name equal to 't' and field DoF equal to 8. When you specify the degrees of freedom, they aren't estimated if you input the model to estimate.
Specify GARCH Model with Nonconsecutive Lags
This example shows how to specify a GARCH model with nonzero coefficients at nonconsecutive lags.
Specify a GARCH(3,1) model with nonzero GARCH coefficients at lags 1 and 3. Include a mean offset.
Mdl = garch('Offset',NaN,'GARCHLags',[1,3],'ARCHLags',1)
Mdl =
garch with properties:
Description: "GARCH(3,1) Conditional Variance Model with Offset (Gaussian Distribution)"
SeriesName: "Y"
Distribution: Name = "Gaussian"
P: 3
Q: 1
Constant: NaN
GARCH: {NaN NaN} at lags [1 3]
ARCH: {NaN} at lag [1]
Offset: NaN
The unknown nonzero GARCH coefficients correspond to lagged variances at lags 1 and 3. The output shows only nonzero coefficients.
Display the value of GARCH.
Mdl.GARCH
ans=1×3 cell array
{[NaN]} {[0]} {[NaN]}
The GARCH cell array returns three elements. The first and third elements have value NaN, indicating these coefficients are nonzero and need to be estimated or otherwise specified. By default, garch sets the interim coefficient at lag 2 equal to zero to maintain consistency with MATLAB® cell array indexing.
What Is a GARCH Model?
A generalized autoregressive conditional heteroscedastic (GARCH) model is a type of conditional variance model, a dynamic model that addresses conditional heteroscedasticity, or volatility clustering, in an innovations process εt. Volatility clustering occurs when an innovations process does not exhibit significant autocorrelation, but the variance of the innovations process changes with time and exhibits autocorrelation.
A GARCH model posits that the current conditional variance is the sum of these linear processes, with coefficients for each term:
Past conditional variances (the GARCH component or polynomial)
Past squared innovations (the ARCH component or polynomial)
Constant offsets for the innovation mean and conditional variance models
Conditional Variance Model
Consider the time series
where . Here, zt is an independent and identically distributed series of standardized random variables (Econometrics Toolbox™ supports standardized Gaussian and standardized Student’s t innovation distributions). The constant term, , is a mean offset.
A conditional variance model specifies the dynamic evolution of the innovation variance,
where Ht–1 is the history of the process. The history includes:
Past variances,
Past innovations,
Conditional variance models are appropriate for time series that do not exhibit significant autocorrelation, but are serially dependent. The innovation series is uncorrelated, because:
E(εt) = 0.
E(εtεt–h) = 0 for all t and
However, if depends on , for example, then εt depends on εt–1, even though they are uncorrelated. This kind of dependence exhibits itself as autocorrelation in the squared innovation series,
GARCH Model
The generalized autoregressive conditional heteroscedastic (GARCH) model is an extension of Engle’s ARCH model for variance heteroscedasticity [1]. If a series exhibits volatility clustering, this suggests that past variances might be predictive of the current variance.
The GARCH(P,Q) model is an autoregressive moving average model for conditional variances, with P GARCH coefficients associated with lagged variances, and Q ARCH coefficients associated with lagged squared innovations. The form of the GARCH(P,Q) model in Econometrics Toolbox is
where and
Note
The Constant property of a garch model corresponds to κ, and the Offset property corresponds to μ.
For stationarity and positivity, the GARCH model has the following constraints:
To specify Engle’s original ARCH(Q) model, use the equivalent GARCH(0,Q) specification.
References
[1] Engle, Robert F. “Autoregressive Conditional Heteroskedasticity with Estimates of the Variance of United Kingdom Inflation.” Econometrica. Vol. 50, 1982, pp. 987–1007.
See Also
Objects
Functions
Related Topics
- Analyze Time Series Data Using Econometric Modeler
- Specifying Univariate Lag Operator Polynomials Interactively
- Modify Properties of Conditional Variance Models
- Specify Conditional Variance Model Innovation Distribution
- Specify Conditional Variance Model for Exchange Rates
- Specify Conditional Mean and Variance Models
