tfest
Estimate transfer function model
Syntax
Description
Estimate Transfer Function Model
sys = tfest(tt,np)sys with
np poles, using all the input and output signals in the timetable
tt. The number of zeros in sys is max(np-1,0).
You can use this syntax for SISO and MISO systems. The function assumes that the last
variable in the timetable is the single output signal.
You cannot use tfest to estimate time-series models, which are
models that contain no inputs. Use ar, arx, or armax for time-series models instead.
sys = tfest(u,y,np)u,y. The software
assumes that the data sample time is 1 second. You cannot change this assumed sample time.
If you want to estimate a model from data with a sample time other than 1 second, you have
two alternatives:
Estimate a discrete-time system instead by setting the sample time using the
'Ts'name-value argument. For example,sys = tfest(u,y,np,'Ts',0.1)sets the sample time to0.1. You can use this syntax with SISO, MISO, and MIMO systems.Convert your matrix data to a
timetableoriddataobject prior to estimating a continuous-time system. These formats allow you to incorporate sample-time knowledge into the data. For more information, seeu,y.
Estimating continuous-time models from matrix-based data is not recommended.
sys = tfest(data,np)data. Use this
syntax especially when you want to estimate a transfer function using frequency-domain or
frequency response data, or when you want to take advantage of the additional information,
such as intersample behavior, data sample time, or experiment labeling, that data objects
provide.
sys = tfest(___,Name,Value)sys = tfest(um,ym,np,'Ts',0.1). Specify input and output signal
variable names that correspond with the variables to use for MIMO timetable data using
sys =
tfest(data,np,nz,'InputNames',["u1","u2"],'OutputNames',["y1","y3"]).
Configure Initial Parameters
Specify Additional Estimation Options
Return Estimated Initial Conditions
[
returns the estimated initial conditions as an sys,ic] = tfest(___)initialCondition
object. Use this syntax if you plan to simulate or predict the model response using the
same estimation input data and then compare the response with the same estimation output
data. Incorporating the initial conditions yields a better match between measured and
simulated or predicted data during the early stage of the simulation.
Examples
Estimate Transfer Function Model by Specifying Number of Poles
Load the time-domain system-response data in timetable tt1.
load sdata1.mat tt1;
Set the number of poles np to 2 and estimate a transfer function.
np = 2; sys = tfest(tt1,np);
sys is an idtf model containing the estimated two-pole transfer function.
View the numerator and denominator coefficients of the resulting estimated model sys.
sys.Numerator
ans = 1×2
2.4554 176.9856
sys.Denominator
ans = 1×3
1.0000 3.1625 23.1631
To view the uncertainty in the estimates of the numerator and denominator and other information, use tfdata.
Specify Number of Poles and Zeros in Estimated Transfer Function
Load time-domain system response data z2 and use it to estimate a transfer function that contains two poles and one zero.
load iddata2 z2; np = 2; nz = 1; sys = tfest(z2,np,nz);
sys is an idtf model containing the estimated transfer function.
Estimate Transfer Function Containing Known Transport Delay
Load the data z2, which is an iddata object that contains time-domain system response data.
load iddata2 z2;
Estimate a transfer function model sys that contains two poles and one zero, and which includes a known transport delay iodelay.
np = 2; nz = 1; iodelay = 0.2; sys = tfest(z2,np,nz,iodelay);
sys is an idtf model containing the estimated transfer function, with the IODelay property set to 0.2 seconds.
Estimate Transfer Function Containing Unknown Transport Delay
Load time-domain system response data z2 and use it to estimate a two-pole one-zero transfer function for the system. Specify an unknown transport delay for the transfer function by setting the value of iodelay to NaN.
load iddata2 z2; np = 2; nz = 1; iodelay = NaN; sys = tfest(z2,np,nz,iodelay);
sys is an idtf model containing the estimated transfer function, whose IODelay property is estimated using the data.
Estimate Discrete-Time Transfer Function
Load time-domain system response data, which is contained in input and output matrices umat2 and ymat2.
load sdata2.mat umat2 ymat2
Estimate a discrete-time transfer function with two poles and one zero. Specify the sample time Ts as 0.1 seconds and the transport delay iodelay as 2 seconds.
np = 2;
nz = 1;
iodelay = 2;
Ts = 0.1;
sysd = tfest(umat2,ymat2,np,nz,iodelay,'Ts',Ts)sysd =
From input "u1" to output "y1":
1.8 z^-1
z^(-2) * ----------------------------
1 - 1.418 z^-1 + 0.6613 z^-2
Sample time: 0.1 seconds
Discrete-time identified transfer function.
Parameterization:
Number of poles: 2 Number of zeros: 1
Number of free coefficients: 3
Use "tfdata", "getpvec", "getcov" for parameters and their uncertainties.
Status:
Estimated using TFEST on time domain data.
Fit to estimation data: 80.26%
FPE: 2.095, MSE: 2.063
By default, the model has no feedthrough, and the numerator polynomial of the estimated transfer function has a zero leading coefficient b0. To estimate b0, specify the Feedthrough property during estimation.
Estimate Discrete-Time Transfer Function with Feedthrough
Load the estimation data z5.
load iddata5 z5
First, estimate a discrete-time transfer function model with two poles, one zero, and no feedthrough. Get the sample time from the Ts property of z5.
np = 2;
nz = 1;
sys = tfest(z5,np,nz,'Ts',z5.Ts);The estimated transfer function has the following form:
By default, the model has no feedthrough, and the numerator polynomial of the estimated transfer function has a zero leading coefficient b0. To estimate b0, specify the Feedthrough property during estimation.
sys = tfest(z5,np,nz,'Ts',z5.Ts,'Feedthrough',true);
The numerator polynomial of the estimated transfer function now has a nonzero leading coefficient:
Analyze Origin of Delay in Measured Data
Compare two discrete-time models with and without feedthrough and transport delay.
If there is a delay from the measured input to output, it can be attributed either to a lack of feedthrough or to an actual transport delay. For discrete-time models, absence of feedthrough corresponds to a lag of one sample between the input and output. Estimating a model using Feedthrough = false and iodelay = 0 thus produces a discrete-time system that is equivalent to a system estimated using Feedthrough = true and iodelay = 1. Both systems show the same time- and frequency-domain responses, for example, on step and Bode plots. However, you get different results if you reduce these models using balred or convert them to their continuous-time representations. Therefore, a best practice is to check if the observed delay can be attributed to a transport delay or to a lack of feedthrough.
Estimate a discrete-time model with no feedthrough.
load iddata1 z1 np = 2; nz = 2; sys1 = tfest(z1,np,nz,'Ts',z1.Ts);
Because sys1 has no feedthrough and therefore has a numerator polynomial that begins with , sys1 has a lag of one sample. The IODelay property is 0.
Estimate another discrete-time model with feedthrough and with a reduction from two zeros to one, incurring a one-sample input-output delay.
sys2 = tfest(z1,np,nz-1,1,'Ts',z1.Ts,'Feedthrough',true);
Compare the Bode responses of the models.
bode(sys1,sys2);
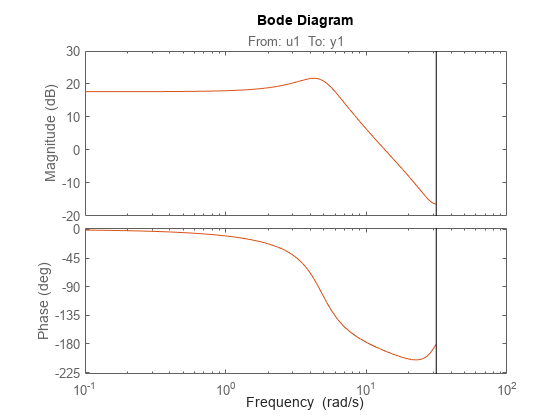
The discrete equations that underlie sys1 and sys2 are equivalent, and so are the Bode responses.
Convert the models to continuous time and compare the Bode responses for these models.
sys1c = d2c(sys1); sys2c = d2c(sys2); bode(sys1c,sys2c); legend
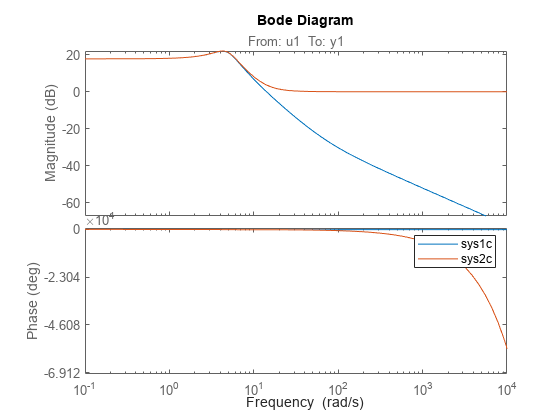
As the plot shows, the Bode responses of the two models do not match when you convert them to continuous time. When there is no feedthrough, as with sys1c, there must be some lag. When there is feedthrough, as with sys2c, there can be no lag. Continuous-time feedthrough maps to discrete-time feedthrough. Continuous-time lag maps to discrete-time delays.
Estimate MISO Discrete-Time Transfer Function with Feedthrough and Delay Specifications for Individual Channels
Estimate a two-input, one-output discrete-time transfer function with a delay of two samples on the first input and zero samples on the second input. Both inputs have no feedthrough.
Load the data and split the data into estimation and validation data sets.
load iddata7 z7 ze = z7(1:300); zv = z7(200:400);
Estimate a two-input, one-output transfer function with two poles and one zero for each input-to-output transfer function.
Lag = [2;0]; Ft = [false,false]; model = tfest(ze,2,1,'Ts',z7.Ts,'Feedthrough',Ft,'InputDelay',Lag);
The Feedthrough value you choose dictates whether the leading numerator coefficient is zero (no feedthrough) or not (nonzero feedthrough). Delays are generally expressed separately using the InputDelay or IODelay property. This example uses InputDelay only to express the delays.
Validate the estimated model. Exclude the data outliers for validation.
I = 1:201;
I(114:118) = [];
opt = compareOptions('Samples',I);
compare(zv,model,opt)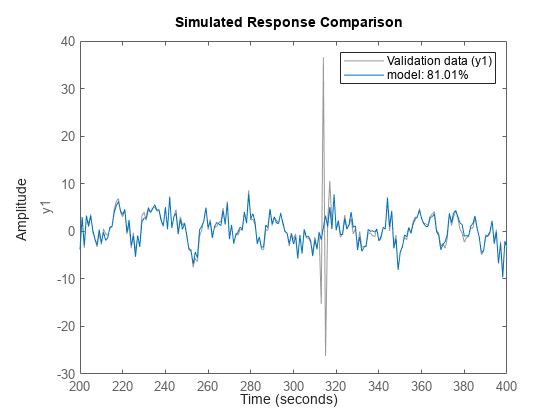
Estimate Transfer Function Model Using Regularized Impulse Response Model
Identify a 15th order transfer function model by using regularized impulse response estimation.
Load the data.
load regularizationExampleData m0simdata;
Obtain a regularized impulse response (FIR) model.
opt = impulseestOptions('RegularizationKernel','DC'); m0 = impulseest(m0simdata,70,opt);
Convert the model into a transfer function model after reducing the order to 15.
m = idtf(balred(idss(m0),15));
Compare the model output with the data.
compare(m0simdata,m);
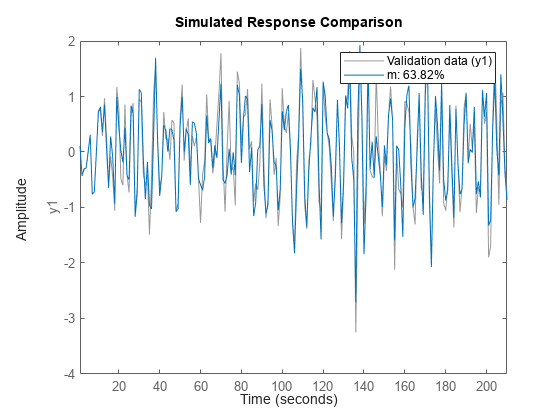
Estimate Transfer Function Using Estimation Option Set
Create an option set for tfest that specifies the initialization and search methods. Also set the display option, which specifies that the loss-function values for each iteration be shown.
opt = tfestOptions('InitializeMethod','n4sid','Display','on','SearchMethod','lsqnonlin');
Load time-domain system response data z2 and use it to estimate a transfer function with two poles and one zero. Specify opt for the estimation options.
load iddata2 z2; np = 2; nz = 1; iodelay = 0.2; sys = tfest(z2,np,nz,iodelay,opt);
sys is an idtf model containing the estimated transfer function.
Specify Model Properties of Estimated Transfer Function
Load the time-domain system response data z2, and use it to estimate a two-pole, one-zero transfer function. Specify an input delay.
load iddata2 z2; np = 2; nz = 1; input_delay = 0.2; sys = tfest(z2,np,nz,'InputDelay',input_delay);
sys is an idtf model containing the estimated transfer function with an input delay of 0.2 seconds.
Convert Frequency-Response Data into Transfer Function
Use bode to obtain the magnitude and phase response for the following system:
Use 100 frequency points, ranging from 0.1 rad/s to 10 rad/s, to obtain the frequency-response data. Use frd to create a frequency-response data object.
freq = logspace(-1,1,100); [mag,phase] = bode(tf([1 0.2],[1 2 1 1]),freq); data = frd(mag.*exp(1j*phase*pi/180),freq);
Estimate a three-pole, one-zero transfer function using data.
np = 3; nz = 1; sys = tfest(data,np,nz);
sys is an idtf model containing the estimated transfer function.
Estimate Transfer Function with Known Transport Delays for Multiple Inputs
Load the time-domain system response data co2data, which contains the data from two experiments, each with two inputs and one output. Convert the data from the first experiment into an iddata object data with a sample time of 0.5 seconds.
load co2data;
Ts = 0.5;
data = iddata(Output_exp1,Input_exp1,Ts);Specify estimation options for the search method and the input and output offsets. Also specify the maximum number of search iterations.
opt = tfestOptions('SearchMethod','gna'); opt.InputOffset = [170;50]; opt.OutputOffset = mean(data.y(1:75)); opt.SearchOptions.MaxIterations = 50;
Estimate a transfer function using the measured data and the estimation option set opt. Specify the transport delays from the inputs to the output.
np = 3; nz = 1; iodelay = [2 5]; sys = tfest(data,np,nz,iodelay,opt);
iodelay specifies the input-to-output delay from the first and second inputs to the output as 2 seconds and 5 seconds, respectively.
sys is an idtf model containing the estimated transfer function.
Estimate Transfer Function with Known and Unknown Transport Delays
Load time-domain system response data and use it to estimate a transfer function for the system. Specify the known and unknown transport delays.
load co2data;
Ts = 0.5;
data = iddata(Output_exp1,Input_exp1,Ts);data is an iddata object with two input channels and one output channels, and which has a sample rate of 0.5 seconds.
Create an option set opt. Specify estimation options for the search method and the input and output offsets. Also specify the maximum number of search iterations.
opt = tfestOptions('Display','on','SearchMethod','gna'); opt.InputOffset = [170; 50]; opt.OutputOffset = mean(data.y(1:75)); opt.SearchOptions.MaxIterations = 50;
Specify the unknown and known transport delays in iodelay, using 2 for a known delay of 2 seconds and nan for the unknown delay. Estimate the transfer function using iodelay and opt.
np = 3; nz = 1; iodelay = [2 nan]; sys = tfest(data,np,nz,iodelay,opt);
sys is an idtf model containing the estimated transfer function.
Estimate Transfer Function with Unknown, Constrained Transport Delays
Create a transfer function model with the expected numerator and denominator structure and delay constraints.
In this example, the experiment data consists of two inputs and one output. Both transport delays are unknown and have an identical upper bound. Additionally, the transfer functions from both inputs to the output are identical in structure.
init_sys = idtf(NaN(1,2),[1,NaN(1,3)],'IODelay',NaN);
init_sys.Structure(1).IODelay.Free = true;
init_sys.Structure(1).IODelay.Maximum = 7;init_sys is an idtf model describing the structure of the transfer function from one input to the output. The transfer function consists of one zero, three poles, and a transport delay. The use of NaN indicates unknown coefficients.
init_sys.Structure(1).IODelay.Free = true indicates that the transport delay is not fixed.
init_sys.Structure(1).IODelay.Maximum = 7 sets the upper bound for the transport delay to 7 seconds.
Specify the transfer function from both inputs to the output.
init_sys = [init_sys,init_sys];
Load time-domain system response data and use it to estimate a transfer function. Specify options in the tfestOptions option set opt.
load co2data; Ts = 0.5; data = iddata(Output_exp1,Input_exp1,Ts); opt = tfestOptions('Display','on','SearchMethod','gna'); opt.InputOffset = [170;50]; opt.OutputOffset = mean(data.y(1:75)); opt.SearchOptions.MaxIterations = 50; sys = tfest(data,init_sys,opt);
sys is an idtf model containing the estimated transfer function.
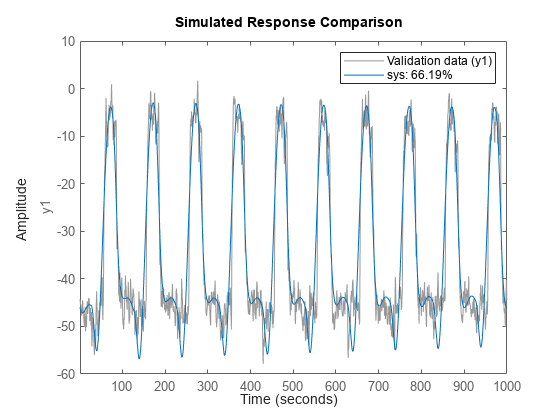
Analyze the estimation result by comparison. Create a compareOptions option set opt2 and specify input and output offsets, and then use compare.
opt2 = compareOptions; opt2.InputOffset = opt.InputOffset; opt2.OutputOffset = opt.OutputOffset; compare(data,sys,opt2)
Estimate Transfer Function Containing Different Numbers of Poles for Input-Output Pairs
Estimate a multiple-input, single-output transfer function containing different numbers of poles for input-output pairs for given data.
Obtain frequency-response data.
For example, use frd to create a frequency-response data model for the following system:
Use 100 frequency points, ranging from 0.01 rad/s to 100 rad/s, to obtain the frequency-response data.
G = tf({[1 2],[5]},{[1 2 4 5],[1 2 1 1 0]},0,'IODelay',[4 0.6]);
data = frd(G,logspace(-2,2,100));data is an frd object containing the continuous-time frequency response for G.
Estimate a transfer function for data.
np = [3 4]; nz = [1 0]; iodelay = [4 0.6]; sys = tfest(data,np,nz,iodelay);
np specifies the number of poles in the estimated transfer function. The first element of np indicates that the transfer function from the first input to the output contains three poles. Similarly, the second element of np indicates that the transfer function from the second input to the output contains four poles.
nz specifies the number of zeros in the estimated transfer function. The first element of nz indicates that the transfer function from the first input to the output contains one zero. Similarly, the second element of np indicates that the transfer function from the second input to the output does not contain any zeros.
iodelay specifies the transport delay from the first input to the output as 4 seconds. The transport delay from the second input to the output is specified as 0.6 seconds.
sys is an idtf model containing the estimated transfer function.
Estimate Transfer Function for Unstable System
Estimate a transfer function describing an unstable system using frequency-response data.
Use idtf to construct a transfer function model G of the following system:
G = idtf({[1 2], 5},{[1 2 4 5],[1 2 1 1 1]});Use idfrd to obtain a frequency-response data model data for G. Specify 100 frequency points ranging from 0.01 rad/s to 100 rad/s.
data = idfrd(G,logspace(-2,2,100));
data is an idfrd object.
Estimate a transfer function for data.
np = [3 4]; nz = [1 0]; sys = tfest(data,np,nz);
np specifies the number of poles in the estimated transfer function. The first element of np indicates that the transfer function from the first input to the output contains three poles. Similarly, the second element of np indicates that the transfer function from the second input to the output contains four poles.
nz specifies the number of zeros in the estimated transfer function. The first element of nz indicates that the transfer function from the first input to the output contains one zero. Similarly, the second element of nz indicates that the transfer function from the second input to the output does not contain any zeros.
sys is an idtf model containing the estimated transfer function.
pole(sys)
ans = 7×1 complex
-1.5260 + 0.0000i
-0.2370 + 1.7946i
-0.2370 - 1.7946i
-1.4656 + 0.0000i
-1.0000 + 0.0000i
0.2328 + 0.7926i
0.2328 - 0.7926i
sys is an unstable system, as the pole display indicates.
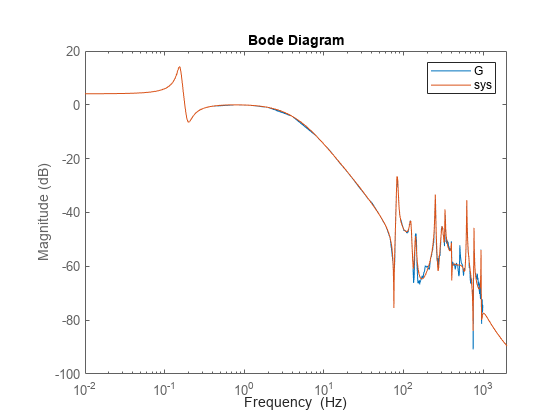
Estimate Transfer Function using High Modal Density Frequency Response Data
Load the high-density frequency-response measurement data. The data corresponds to an unstable process maintained at equilibrium using feedback control.
load HighModalDensityData FRF f
Package the data as an idfrd object for identification and find the Bode magnitude response.
G = idfrd(permute(FRF,[2 3 1]),f,0,'FrequencyUnit','Hz'); bodemag(G)

Estimate a transfer function with 32 poles and 32 zeros, and compare the Bode magnitude response.
sys = tfest(G,32,32); bodemag(G, sys) xlim([0.01,2e3]) legend
Obtain and Apply Estimated Initial Conditions
Load and plot the data.
load iddata1ic z1i plot(z1i)

Examine the initial value of the output data y(1).
ystart = z1i.y(1)
ystart = -3.0491
The measured output does not start at 0.
Estimate a second-order transfer function sys and return the estimated initial condition ic.
[sys,ic] = tfest(z1i,2,1); ic
ic =
initialCondition with properties:
A: [2x2 double]
X0: [2x1 double]
C: [0.2957 5.2441]
Ts: 0
ic is an initialCondition object that encapsulates the free response of sys, in state-space form, to the initial state vector in X0.
Simulate sys using the estimation data but without incorporating the initial conditions. Plot the simulated output with the measured output.
y_no_ic = sim(sys,z1i); plot(y_no_ic,z1i) legend('Model Response','Output Data')
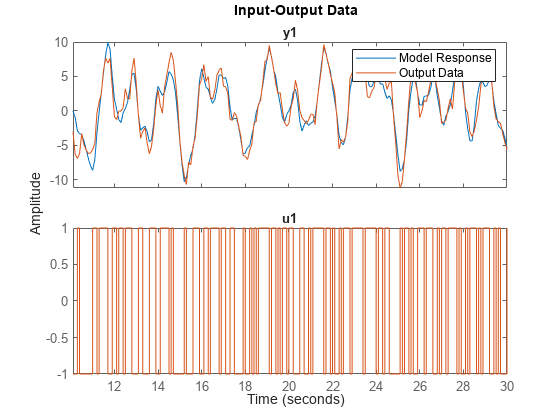
The measured and simulated outputs do not agree at the beginning of the simulation.
Incorporate the initial condition into the simOptions option set.
opt = simOptions('InitialCondition',ic); y_ic = sim(sys,z1i,opt); plot(y_ic,z1i) legend('Model Response','Output Data')

The simulation combines the model response to the input signal with the free response to the initial condition. The measured and simulated outputs now have better agreement at the beginning of the simulation. This initial condition is valid only for the estimation data z1i.
Input Arguments
tt — Timetable-based estimation data
timetable | cell array of timetables
Estimation data, specified as a uniformly sampled timetable
that contains both input and output signal variables
or, for multiexperiment data, a cell array of
timetables.
Use Entire Timetable
If you want to use all the input and output variables in tt, and the
variables are organized so that the set of input
variables is followed by the set of output
variables, then:
For SISO systems, specify
ttas an Ns-by-2timetable, where Ns is the number of samples and the twotimetablevariables represent the measured input signal and output signal respectively.For MIMO systems, specify
ttas an Ns-by-(Nu+Ny)timetable, where Nu is the number of inputs and Ny is the number of outputs. The first Nu variables must contain the input signals and the remaining Ny variables must contain the output signals.When you are estimating state space or transfer function models, you must also explicitly specify the input and output channels, as the following section describes.
For multiexperiment data, specify data as an Ne-by-1 cell array of timetables, where Ne is the number of experiments. The sample times of all the experiments must match.
Use Selected Variables from Timetable
If you want to use a subset of variables from the timetable, or if the input
and output variables are intermixed, use the
'InputName' and
'OutputName' name-value
arguments to specify which variables to
use.
For example, suppose that tt contains six variables:
"u1", "u2", "u3", and
"y1", "y2", "y3". For estimation,
you want to use the variables "u1" and "u2" as the
inputs and the variables "y1" and "y3" as the outputs.
Use the following command to perform the estimation:
sys = tfest(tt,__,'InputName',["u1" "u2"],'OutputName',["y1"
"y3"])
For more information about working with estimation data types, see Data Domains and Data Types in System Identification Toolbox.
u, y — Matrix-based estimation data
matrices | cell array of matrices
Estimation data, specified for SISO systems as a pair of Ns-by-1 real-valued matrices that contain uniformly sampled input and output time-domain signal values. Here, Ns is the number of samples.
For MIMO systems, specify u,y as an
input/output matrix pair with the following dimensions:
u— Ns-by-Nu, where Nu is the number of inputs.y— Ns-by-Ny, where Ny is the number of outputs.
For multiexperiment data, specify u,y as a
pair of 1-by-Ne cell arrays, where
Ne is the number of experiments. The
sample times of all the experiments must match.
Limitations
Matrix-based data does not support estimation from frequency-domain data. You must use a data object such as an
iddataobject oridfrdobject (seedata).Using matrices for estimation data is not recommended for continuous-time estimation since the data does not provide the sample time. The software assumes that the data is sampled at 1 Hz. For continuous-time estimation, it is recommended that you convert the input and output matrix pair into a single
timetable. For example, to convert the single-column matricesumandymto atimetablettwith a sample time of 0.5 minutes, use the following command.For a more detailed example of converting matrix-based SISO data to a timetable, see Convert SISO Matrix Data to Timetable. For an example of converting a MIMO matrix pair to a timetable, see Convert MIMO Matrix Data to Timetable for Continuous-Time Model Estimation.tt = timetable(um,ym,'rowtimes',minutes(0.5*(1:size(u,1))))For more information about working with estimation data types, see Data Domains and Data Types in System Identification Toolbox.
data — Estimation data object
iddata object | frd object | idfrd object
Estimation data object, specified as an iddata object, an
frd object, or an idfrd object that contains
uniformly sampled input and output values. By default, the software sets the sample time
of the model to the sample time of the estimation data.
For multiexperiment data, the sample times and intersample behavior of all the experiments must match.
For time-domain estimation, data must be an iddata object containing the input and output signal values.
For frequency-domain estimation, data can be one of the
following:
Limitations
You cannot estimate continuous-time models using discrete-time frequency-domain data.
np — Number of poles
nonnegative integer | matrix
Number of poles in the estimated transfer function, specified as a nonnegative integer or a matrix.
For systems that have multiple inputs and/or multiple outputs, you can apply either
a global value or individual values of np to the input/output
pairs, as follows:
Same number of poles for every pair — Specify
npas a scalar.Individual number of poles for each pair — Specify
npas an Ny-by-Nu matrix. Ny is the number of outputs and Nu is the number of inputs.
For an example, see Estimate Transfer Function Model by Specifying Number of Poles.
nz — Number of zeros
nonnegative integer | matrix
Number of zeros in the estimated transfer function, specified as a nonnegative integer or a matrix.
For systems that have multiple inputs, multiple outputs, or both, you can apply
either a global value or individual values of nz to the
input/output pairs, as follows:
Same number of poles for every pair — Specify
nzas a scalar.Individual number of poles for each pair — Specify
nzas an Ny-by-Nu matrix. Ny is the number of outputs and Nu is the number of inputs.
For a continuous-time model estimated using discrete-time data, set
nz <= np.
For discrete-time model estimation, specify nz as the number of
zeros of the numerator polynomial of the transfer function. For example,
tfest(tt,2,1,'Ts',data.Ts) estimates a transfer function of the
form , while tfest(tt,2,2,'Ts',data.Ts) estimates . Here, z-1 is the
Z-transform lag variable. For more information about discrete-time transfer functions,
see Discrete-Time Representation. For an example, see Estimate Discrete-Time Transfer Function.
iodelay — Transport delay
[] (default) | nonnegative integer | matrix
Transport delay, specified as a nonnegative integer, a NaN
scalar, or a matrix.
For continuous-time systems, specify transport delays in the time unit stored in the
TimeUnit property of data. For discrete-time
systems, specify transport delays as integers denoting delays of a multiple of the
sample time Ts.
For a MIMO system with Ny outputs and
Nu inputs, set
iodelay to an
Ny-by-Nu
array. Each entry of this array is a numerical value that represents the transport delay
for the corresponding input/output pair. You can also set iodelay
to a scalar value to apply the same delay to all input/output pairs.
The specified values are treated as fixed delays. To denote unknown transport
delays, specify NaN in the iodelay
matrix.
Use [] or 0 to indicate no transport
delay.
For an example, see Estimate Transfer Function Containing Known Transport Delay.
opt — Estimation options
tfestOptions option set
Estimation options, specified as a tfestOptions option set. Options specified by opt
include:
Estimation objective
Handling of initial conditions
Numerical search method to be used in estimation
Intersample behavior
For an example, see Estimate Transfer Function Using Estimation Option Set.
init_sys — Linear system that configures initial parameterization of sys
idtf model | linear model | structure
Linear system that configures the initial parameterization of
sys, specified as an idtf model, a linear model , or a
structure. You obtain init_sys either by performing an estimation
using measured data or by direct construction.
If init_sys is an idtf model,
tfest uses the parameter values of init_sys
as the initial guess for estimating sys.
Use the Structure property of init_sys to
configure initial parameter values and constraints for the numerator, denominator, and
transport lag. For instance:
To specify an initial guess for the A matrix of
init_sys, setinit_sys.Structure.Numerator.Valueto the initial guess.To specify constraints for the B matrix of
init_sys:Set
init_sys.Structure.Numerator.Minimumto the minimum numerator coefficient values.Set
init_sys.Structure.Numerator.Maximumto the maximum numerator coefficient values.Set
init_sys.Structure.Numerator.Freeto indicate which numerator coefficients are free for estimation.
For an example, see Estimate Transfer Function with Unknown, Constrained Transport Delays.
If
init_sys is not an idtf model, the software
first converts init_sys to a transfer function.
tfest uses the parameters of the resulting model as the initial
guess for estimation.
If you do not specify opt, and init_sys
was obtained by estimation rather than construction, then the software uses estimation
options from init_sys.Report.OptionsUsed.
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: sys = tfest(data,np,nz,'Ts',0.1)
InputName — Input channel names
string | character vector | string array | cell array of character vectors
Input channel names, specified as a string, character vector, string array, or cell array of character vectors.
If you are using a timetable for the data source, the names in
InputName must be a subset of the timetable variables.
Example: sys = tfest(tt,__,'InputName',["u1" "u2"]) selects
the variables u1 and u2 as the input channels from
the timetable tt to use for the estimation.
OutputName — Output channel names
string | character vector | string array | cell array of character vectors
Output channel names, specified as a string, character vector, string array, or cell array of character vectors.
If you are using a timetable for the data source, the names in
OutputName must be a subset of the timetable variables.
Example: sys = tfest(tt,__,'OutputName',["y1" "y3"]) selects
the variables y1 and y3 as the output channels
from the timetable tt to use for the estimation.
Ts — Sample time of estimated model
0 (continuous time) (default) | positive scalar
Sample time of the estimated model, specified as either 0 or a
positive scalar.
For continuous-time models, specify
'Ts'as0.For discrete-time models, specify
'Ts'as the data sample time in units defined by the following:For timetable-based data — The timetable
TimecolumnFor matrix-based data — Seconds
For data objects, such as
iddataobjects — Thedata.TimeUnitproperty
In the discrete case,
npandnzrefer to the number of roots of z-1 for the numerator and denominator polynomials.To obtain the data sample time for a timetable
tt, use the timetable propertytt.Properties.Timestep.
For an example, see Estimate Discrete-Time Transfer Function.
InputDelay — Input delays
0
(default) | scalar | vector
Input delay for each input channel, specified as a scalar or a numeric vector.
For continuous-time models, specify
'InputDelay'in the time units stored in theTimeUnitproperty.For discrete-time models, specify
'InputDelay'in integer multiples of the sample timeTs. For example, setting'InputDelay'to3specifies a delay of three sampling periods.
For a system with Nu inputs, set
InputDelay to an
Nu-by-1 vector. Each entry of this vector is
a numerical value that represents the input delay for the corresponding input
channel.
To apply the same delay to all channels, specify InputDelay
as a scalar.
For an example, see Specify Model Properties of Estimated Transfer Function.
Feedthrough — Feedthrough for discrete-time transfer function
0 (default) | 1 | logical matrix
Feedthrough for discrete-time transfer functions, specified as a logical scalar or
an
Ny-by-Nu
logical matrix. Ny is the number of outputs
and Nu is the number of inputs. To use the
same feedthrough for all input/output channels, specify Feedthrough
as a scalar.
Consider a discrete-time model with two poles and three zeros:
When the model has direct feedthrough, b0 is a free parameter whose value is estimated along with the rest of the model parameters b1, b2, b3, a1, and a2. When the model has no feedthrough, b0 is fixed to zero. For an example, see Estimate Discrete-Time Transfer Function with Feedthrough.
Output Arguments
sys — Identified transfer function
idtf model
Identified transfer function, returned as an idtf model. This model is created using the specified model orders, delays,
and estimation options.
Information about the estimation results and options used is stored in the
Report property of the model. Report has the
following fields.
| Report Field | Description |
|---|---|
Status | Summary of the model status, which indicates whether the model was created by construction or obtained by estimation |
Method | Estimation command used |
InitializeMethod | Algorithm used to initialize the numerator and denominator for estimation of continuous-time transfer functions using time-domain data, returned as one of the following values:
This field is especially useful to view the algorithm used
when the |
N4Weight | Weighting matrices used in the singular-value decomposition step when
This field is especially useful to view the weighting
matrices used when the |
N4Horizon | Forward and backward prediction horizons used when
|
InitialCondition | Handling of initial conditions during model estimation, returned as one of the following values:
This field is especially useful to view
how the initial conditions were handled when the |
Fit | Quantitative assessment of the estimation, returned as a structure. See Loss Function and Model Quality Metrics for more information on these quality metrics. The structure has these fields.
|
Parameters | Estimated values of model parameters |
OptionsUsed | Option set used for estimation. If no custom options were configured,
this is a set of default options. See |
RandState | State of the random number stream at the start of estimation. Empty,
|
DataUsed | Attributes of the data used for estimation, returned as a structure with the following fields.
|
Termination | Termination conditions for the iterative search used for prediction error minimization, returned as a structure with these fields.
For estimation methods that do not require numerical search
optimization, the |
For more information on using Report, see Estimation Report.
ic — Initial conditions
initialCondition object | object array of initialCondition values
Estimated initial conditions, returned as an initialCondition object or an object array of
initialCondition values.
For a single-experiment data set,
icrepresents, in state-space form, the free response of the transfer function model (A and C matrices) to the estimated initial states (x0).For a multiple-experiment data set with Ne experiments,
icis an object array of length Ne that contains one set ofinitialConditionvalues for each experiment.
If tfest returns ic values of
0 and you know that you have non-zero initial conditions, set the
'InitialCondition' option in tfestOptions to 'estimate' and pass the updated option
set to tfest. For
example:
opt = tfestOptions('InitialCondition','estimate') [sys,ic] = tfest(data,np,nz,opt)
'auto' setting of 'InitialCondition' uses
the 'zero' method when the initial conditions have a negligible
effect on the overall estimation-error minimization process. Specifying
'estimate' ensures that the software estimates values for
ic.
For more information, see initialCondition. For an example of using this argument, see Obtain and Apply Estimated Initial Conditions.
Algorithms
The details of the estimation algorithms used by tfest vary depending
on various factors, including the sampling of the estimated model and the estimation
data.
Continuous-Time Transfer Function Estimation Using Time-Domain Data
The estimation algorithm initializes the estimable parameters using the method
specified by the InitializeMethod estimation option. The default method
is the Instrument Variable (IV) method.
The State-Variable Filters (SVF) approach and the Generalized Poisson Moment Functions
(GPMF) approach to continuous-time parameter estimation use prefiltered data [1]
[2]. The constant in [1] and [2] corresponds to the initialization option (InitializeOptions) field
FilterTimeConstant. IV is the simplified refined IV method and is
called SRIVC in [3]. This method has a prefilter that is the denominator of the current model, initialized
with SVF. This prefilter is iterated up to MaxIterations times, until
the model change is less than Tolerance.
MaxIterations and Tolerance are options that you
can specify using the InitializeOptions structure. The
'n4sid' initialization option estimates a discrete-time model, using
the N4SID estimation algorithm, that it transforms to continuous-time using d2c.
Use tfestOptions to create the option set used
to estimate a transfer function.
The initialized parameters are updated using a nonlinear least-squares search method,
specified by the SearchMethod estimation option. The objective of the
search method is to minimize the weighted prediction error norm.
Discrete-Time Transfer Function Estimation Using Time-Domain Data
Continuous-Time Transfer Function Estimation Using Continuous-Time Frequency-Domain Data
The estimation algorithm performs the following tasks:
Perform a bilinear mapping to transform the domain (frequency grid) of the transfer function. For continuous-time models, the imaginary axis is transformed to the unit disk. For discrete-time models, the original domain unit disk is transformed to another unit disk.
Perform S-K iterations [4] to solve a nonlinear least-squares problem — Consider a multi-input single-output system. The nonlinear least-squares problem is to minimize the following loss function:
Here, W is a frequency-dependent weight that you specify. D is the denominator of the transfer function model that is to be estimated, and Ni is the numerator corresponding to the ith input. y and u are the measured output and input data, respectively. nf and nu are the number of frequencies and inputs, and w is the frequency. Rearranging the terms gives
To perform the S-K iterations, the algorithm iteratively solves
Here, m is the current iteration, and Dm-1(ω) is the denominator response identified at the previous iteration. Now each step of the iteration is a linear least-squares problem, where the identified parameters capture the responses Dm(ω) and Ni,m(ω) for i = 1,2,...nu. The iteration is initialized by choosing D0(ω) = 1.
The first iteration of the algorithm identifies D1(ω). The D1(ω) and Ni,1(ω) polynomials are expressed in monomial basis.
The second and following iterations express the polynomials Dm(ω) and Ni,m(ω) in terms of orthogonal rational basis functions on the unit disk. These basis functions have the form
Here, λj,m-1 is the jth pole that is identified at the previous step m-1 of the iteration. λj,m-1* is the complex conjugate of λj,m-1, and q is the frequency-domain variable on the unit disk.
The algorithm runs for a maximum of 20 iterations. The iterations are terminated early if the relative change in the value of the loss function is less than 0.001 in the last three iterations.
If you specify bounds on transfer function coefficients, these bounds correspond to affine constraints on the identified parameters. If you have only equality constraints (fixed transfer function coefficients), the corresponding equality constrained least-squares problem is solved algebraically. To do so, the software computes an orthogonal basis for the null space of the equality constraint matrix, and then solves the least-squares problem within this null space. If you have upper or lower bounds on transfer function coefficients, the corresponding inequality constrained least-squares problem is solved using interior-point methods.
Perform linear refinements — The S-K iterations, even when they converge, do not always yield a locally optimal solution. To find a critical point of the optimization problem that can yield a locally optimal solution, a second set of iterations are performed. The critical points are solutions to a set of nonlinear equations. The algorithm searches for a critical point by successively constructing a linear approximation to the nonlinear equations and solving the resulting linear equations in the least-squares sense. The equations follow.
Equation for the jth denominator parameter:
Equation for the jth numerator parameter that corresponds to input l:
The first iteration is started with the best solution found for the numerators Ni and denominator D parameters during S-K iterations. Unlike S-K iterations, the basis functions Bj(ω) are not changed at each iteration; the iterations are performed with the basis functions that yielded the best solution in the S-K iterations. As before, the algorithm runs for a maximum of 20 iterations. The iterations are terminated early if the relative change in the value of the loss function is less than 0.001 in the last three iterations.
If you specify bounds on transfer function coefficients, these bounds are incorporated into the necessary optimality conditions using generalized Lagrange multipliers. The resulting constrained linear least-squares problems are solved using the same methods explained in the S-K iterations step.
Return the transfer function parameters corresponding to the optimal solution — Both the S-K and linear refinement iteration steps do not guarantee an improvement in the loss function value. The algorithm tracks the best parameter value observed during these steps, and returns these values.
Invert the bilinear mapping performed in step 1.
Perform an iterative refinement of the transfer function parameters using the nonlinear least-squares search method specified in the
SearchMethodestimation option. This step is implemented in the following situations:When you specify the
EnforceStabilityestimation option astrue(stability is requested), and the result of step 5 of this algorithm is an unstable model. The unstable poles are reflected inside the stability boundary and the resulting parameters are iteratively refined. For information about estimation options, seetfestOptions.When you add a regularization penalty to the loss function using the
Regularizationestimation option. For an example about regularization, see Regularized Identification of Dynamic Systems.You estimate a continuous-time model using discrete-time data (see Discrete-Time Transfer Function Estimation Using Discrete-Time Frequency-Domain Data).
You use frequency domain input/output data to identify a multi-input model.
If you are using the estimation algorithm from R2016a or earlier (see tfest Estimation Algorithm Update) for estimating a continuous-time model using continuous-time frequency-domain data, then for continuous-time data and fixed delays, the Output-Error algorithm is used for model estimation. For continuous-time data and free delays, the state-space estimation algorithm is used. In this algorithm, the model coefficients are initialized using the N4SID estimation method. This initialization is followed by nonlinear least-squares search-based updates to minimize a weighted prediction error norm.
Discrete-Time Transfer Function Estimation Using Discrete-Time Frequency-Domain Data
The estimation algorithm is the same as for continuous-time transfer function estimation using continuous-time frequency-domain data, except discrete-time data is used.
If you are using the estimation algorithm from R2016a or earlier (see tfest Estimation Algorithm Update), the algorithm is the same as the algorithm for discrete-time transfer function estimation using time-domain data.
Note
The software does not support estimation of a discrete-time transfer function using continuous-time frequency-domain data.
Continuous-Time Transfer Function Estimation Using Discrete-Time Frequency-Domain Data
The tfest command first estimates a discrete-time model from the
discrete-time data. The estimated model is then converted to a continuous-time model using
the d2c command. The frequency response of the
resulting continuous-time model is then computed over the frequency grid of the estimation
data. A continuous-time model of the desired (user-specified) structure is then fit to this
frequency response. The estimation algorithm for using the frequency-response data to obtain
the continuous-time model is the same as the algorithm for continuous-time transfer function
estimation using continuous-time data.
If you are using the estimation algorithm from R2016a or earlier (see tfest Estimation Algorithm Update), the state-space estimation algorithm is used for estimating continuous-time models from discrete-time data. In this algorithm, the model coefficients are initialized using the N4SID estimation method. This initialization is followed by nonlinear least-squares search-based updates to minimize a weighted prediction error norm.
Delay Estimation
When delay values are specified as
NaN, the software usesdelayestto estimate them separately from the model numerator and denominator coefficients.tfestthen treats these delay values as fixed during the iterative update of the rest of the model. Therefore, the delay values are not iteratively updated.By default, for discrete-time data (
Ts>0),delayestlimits the search for delays to a range of 0–30 samples. For continuous-time models, this range translates to 0–30Tstime units. For continuous-time data (Ts= 0),delayestlimits the search range to 0–10 time units. You can change these limits by first creating a template modelinit_sysusingidtfand then, setting the values ofinit_sys.Structure.IODelay.Minimumandinit_sys.Structure(i,j).IODelay.Maximum.For an initial model,
init_sys, with:init_sys.Structure.IODelay.Valuespecified as finite valuesinit_sys.Structure.IODelay.Freespecified astrue
the initial delay values are left unchanged.
Estimation of delays is often a difficult problem. A best practice is to assess the
presence and the value of a delay. To do so, use physical insight of the process being
modeled and functions such as arxstruc, delayest, and impulseest. For an example of determining
input delay, see Model Structure Selection: Determining Model Order and Input Delay.
References
[1] Garnier, H., M. Mensler, and A. Richard. “Continuous-Time Model Identification from Sampled Data: Implementation Issues and Performance Evaluation.” International Journal of Control 76, no. 13 (January 2003): 1337–57. https://doi.org/10.1080/0020717031000149636.
[2] Ljung, Lennart. “Experiments with Identification of Continuous Time Models.” IFAC Proceedings Volumes 42, no. 10 (2009): 1175–80. https://doi.org/10.3182/20090706-3-FR-2004.00195.
[3] Young, Peter, and Anthony Jakeman. “Refined Instrumental Variable Methods of Recursive Time-Series Analysis Part III. Extensions.” International Journal of Control 31, no. 4 (April 1980): 741–64. https://doi.org/10.1080/00207178008961080.
[4] Drmač, Z., S. Gugercin, and C. Beattie. “Quadrature-Based Vector Fitting for Discretized H2 Approximation.” SIAM Journal on Scientific Computing 37, no. 2 (January 2015): A625–52. https://doi.org/10.1137/140961511.
[5] Ozdemir, Ahmet Arda, and Suat Gumussoy. “Transfer Function Estimation in System Identification Toolbox via Vector Fitting.” IFAC-PapersOnLine 50, no. 1 (July 2017): 6232–37. https://doi.org/10.1016/j.ifacol.2017.08.1026.
Version History
Introduced in R2012aR2022b: Time-domain estimation data is accepted in the form of timetables and matrices
Most estimation, validation, analysis, and utility functions now accept time-domain
input/output data in the form of a single timetable that contains both input and output data
or a pair of matrices that contain the input and output data separately. These functions
continue to accept iddata objects as a data source as well, for
both time-domain and frequency-domain data.
R2018a: Advanced Options are deprecated for SearchOptions when SearchMethod is 'lsqnonlin'
Specification of lsqnonlin- related advanced options are deprecated,
including the option to invoke parallel processing when estimating using the
lsqnonlin search method, or solver, in Optimization Toolbox™.
R2016b: tfest Estimation Algorithm Update
Starting in R2016b, a new algorithm is used for performing transfer function estimation
from frequency-domain data. You are likely to see faster and more accurate results with the
new algorithm, particularly for data with dynamics over a large range of frequencies and
amplitudes. However, the estimation results might not match results from previous releases.
To perform estimation using the previous estimation algorithm, append
'-R2016a' to the syntax.
For example, suppose that you are estimating a transfer function model with
np poles using the frequency-domain data
data.
sys = tfest(data,np)
To use the previous estimation algorithm, use the following syntax.
sys = tfest(data,np,'-R2016a')See Also
tfestOptions | idtf | timetable | ssest | procest | ar | arx | oe | bj | polyest | greyest
Topics
- Estimate Transfer Function Models at the Command Line
- Estimate Transfer Function Models with Transport Delay to Fit Given Frequency-Response Data
- Estimate Transfer Function Models with Prior Knowledge of Model Structure and Constraints
- Apply Initial Conditions When Simulating Identified Linear Models
- Troubleshoot Frequency-Domain Identification of Transfer Function Models
- What are Transfer Function Models?
- Regularized Estimates of Model Parameters
- Estimating Models Using Frequency-Domain Data
Commande MATLAB
Vous avez cliqué sur un lien qui correspond à cette commande MATLAB :
Pour exécuter la commande, saisissez-la dans la fenêtre de commande de MATLAB. Les navigateurs web ne supportent pas les commandes MATLAB.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)