erf
Error function
Syntax
Description
erf( returns the Error Function evaluated for each element
of x)x.
Examples
Find Error Function
Find the error function of a value.
erf(0.76)
ans = 0.7175
Find the error function of the elements of a vector.
V = [-0.5 0 1 0.72]; erf(V)
ans = 1×4
-0.5205 0 0.8427 0.6914
Find the error function of the elements of a matrix.
M = [0.29 -0.11; 3.1 -2.9]; erf(M)
ans = 2×2
0.3183 -0.1236
1.0000 -1.0000
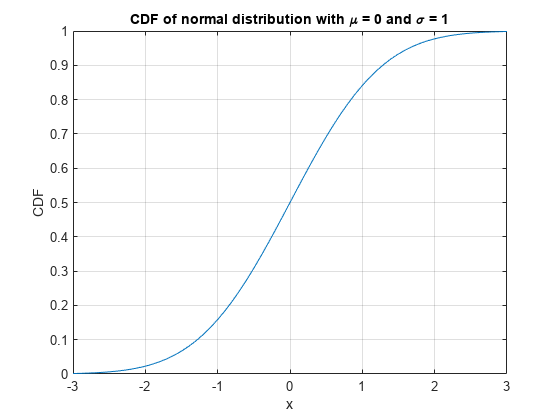
Find Cumulative Distribution Function of Normal Distribution
The cumulative distribution function (CDF) of the normal, or Gaussian, distribution with standard deviation and mean is
Note that for increased computational accuracy, you can rewrite the formula in terms of erfc. For details, see Tips.
Plot the CDF of the normal distribution with and .
x = -3:0.1:3; y = (1/2)*(1+erf(x/sqrt(2))); plot(x,y) grid on title('CDF of normal distribution with \mu = 0 and \sigma = 1') xlabel('x') ylabel('CDF')
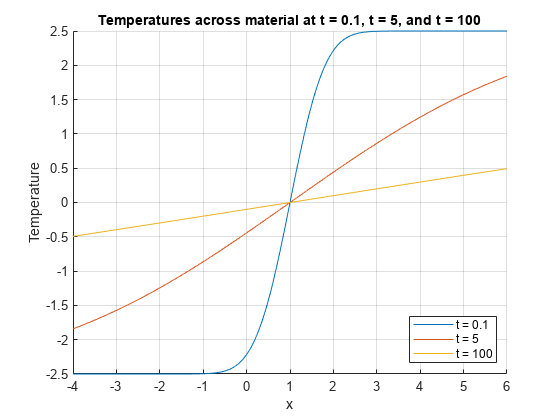
Calculate Solution of Heat Equation with Initial Condition
Where represents the temperature at position and time , the heat equation is
where is a constant.
For a material with heat coefficient , and for the initial condition for and elsewhere, the solution to the heat equation is
For k = 2, a = 5, and b = 1, plot the solution of the heat equation at times t = 0.1, 5, and 100.
x = -4:0.01:6; t = [0.1 5 100]; a = 5; k = 2; b = 1; figure(1) hold on for i = 1:3 u(i,:) = (a/2)*(erf((x-b)/sqrt(4*k*t(i)))); plot(x,u(i,:)) end grid on xlabel('x') ylabel('Temperature') legend('t = 0.1','t = 5','t = 100','Location','best') title('Temperatures across material at t = 0.1, t = 5, and t = 100')
Input Arguments
x — Input
real number | vector of real numbers | matrix of real numbers | multidimensional array of real numbers
Input, specified as a real number, or a vector, matrix, or multidimensional
array of real numbers. x cannot be sparse.
Data Types: single | double
More About
Error Function
The error function erf of x is
Tips
You can also find the standard normal probability distribution using the function
normcdf(Statistics and Machine Learning Toolbox). The relationship between the error functionerfandnormcdfisFor expressions of the form
1 - erf(x), use the complementary error functionerfcinstead. This substitution maintains accuracy. Whenerf(x)is close to1, then1 - erf(x)is a small number and might be rounded down to0. Instead, replace1 - erf(x)witherfc(x).
Extended Capabilities
Tall Arrays
Calculate with arrays that have more rows than fit in memory.
This function fully supports tall arrays. For more information, see Tall Arrays.
C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.
Usage notes and limitations:
Strict single-precision calculations are not supported. In the generated code, single-precision inputs produce single-precision outputs. However, variables inside the function might be double-precision.
Thread-Based Environment
Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool.
This function fully supports thread-based environments. For more information, see Run MATLAB Functions in Thread-Based Environment.
GPU Arrays
Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.
This function fully supports GPU arrays. For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Distributed Arrays
Partition large arrays across the combined memory of your cluster using Parallel Computing Toolbox™.
This function fully supports distributed arrays. For more information, see Run MATLAB Functions with Distributed Arrays (Parallel Computing Toolbox).
Version History
Introduced before R2006a
Commande MATLAB
Vous avez cliqué sur un lien qui correspond à cette commande MATLAB :
Pour exécuter la commande, saisissez-la dans la fenêtre de commande de MATLAB. Les navigateurs web ne supportent pas les commandes MATLAB.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)