fitctree
Fit binary decision tree for multiclass classification
Syntax
Description
tree = fitctree(Tbl,ResponseVarName)Tbl and output (response or labels) contained in
Tbl.ResponseVarName. The returned binary tree splits
branching nodes based on the values of a column of
Tbl.
tree = fitctree(___,Name,Value)
Examples
Grow a Classification Tree
Grow a classification tree using the ionosphere data set.
load ionosphere
tc = fitctree(X,Y)tc =
ClassificationTree
ResponseName: 'Y'
CategoricalPredictors: []
ClassNames: {'b' 'g'}
ScoreTransform: 'none'
NumObservations: 351
Control Tree Depth
You can control the depth of the trees using the MaxNumSplits, MinLeafSize, or MinParentSize name-value pair parameters. fitctree grows deep decision trees by default. You can grow shallower trees to reduce model complexity or computation time.
Load the ionosphere data set.
load ionosphereThe default values of the tree depth controllers for growing classification trees are:
n - 1forMaxNumSplits.nis the training sample size.1forMinLeafSize.10forMinParentSize.
These default values tend to grow deep trees for large training sample sizes.
Train a classification tree using the default values for tree depth control. Cross-validate the model by using 10-fold cross-validation.
rng(1); % For reproducibility MdlDefault = fitctree(X,Y,'CrossVal','on');
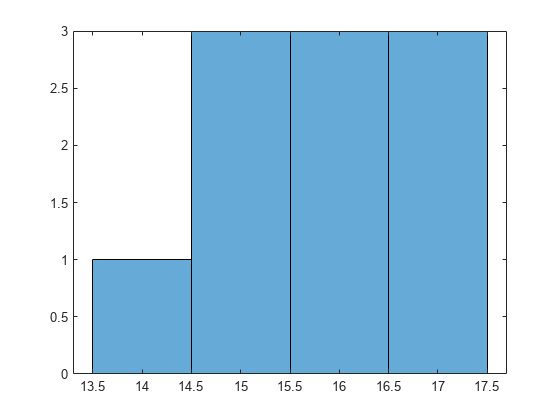
Draw a histogram of the number of imposed splits on the trees. Also, view one of the trees.
numBranches = @(x)sum(x.IsBranch); mdlDefaultNumSplits = cellfun(numBranches, MdlDefault.Trained); figure; histogram(mdlDefaultNumSplits)
view(MdlDefault.Trained{1},'Mode','graph')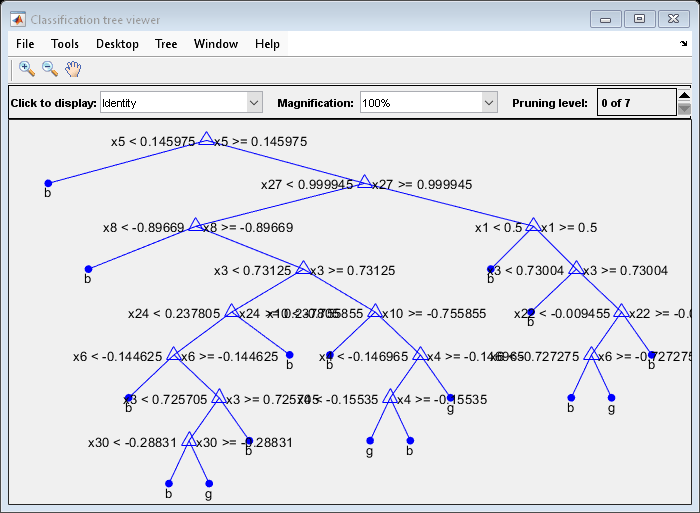
The average number of splits is around 15.
Suppose that you want a classification tree that is not as complex (deep) as the ones trained using the default number of splits. Train another classification tree, but set the maximum number of splits at 7, which is about half the mean number of splits from the default classification tree. Cross-validate the model by using 10-fold cross-validation.
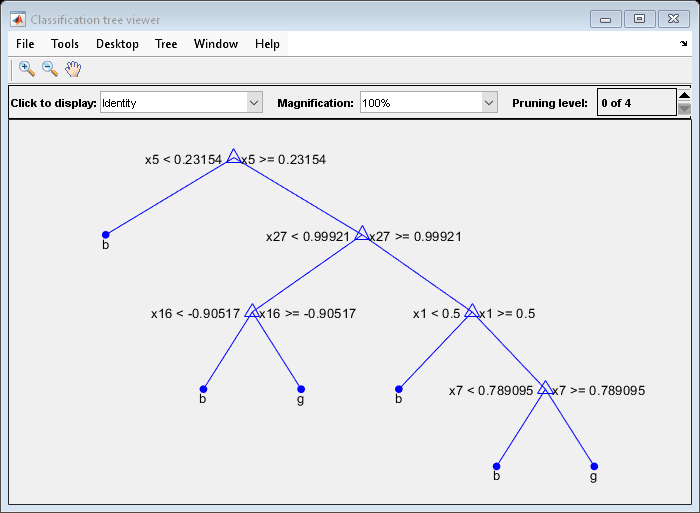
Mdl7 = fitctree(X,Y,'MaxNumSplits',7,'CrossVal','on'); view(Mdl7.Trained{1},'Mode','graph')
Compare the cross-validation classification errors of the models.
classErrorDefault = kfoldLoss(MdlDefault)
classErrorDefault = 0.1168
classError7 = kfoldLoss(Mdl7)
classError7 = 0.1311
Mdl7 is much less complex and performs only slightly worse than MdlDefault.
Optimize Classification Tree
This example shows how to optimize hyperparameters automatically using fitctree. The example uses Fisher's iris data.
Load Fisher's iris data.
load fisheririsOptimize the cross-validation loss of the classifier, using the data in meas to predict the response in species.
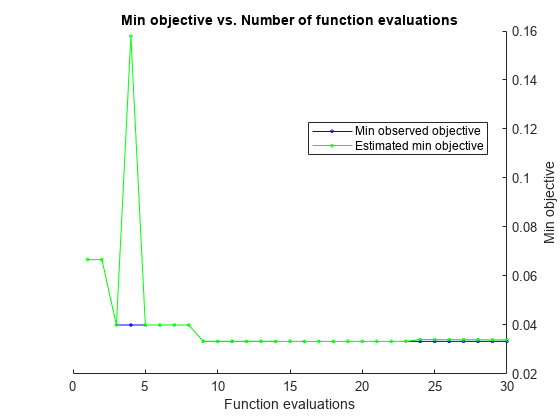
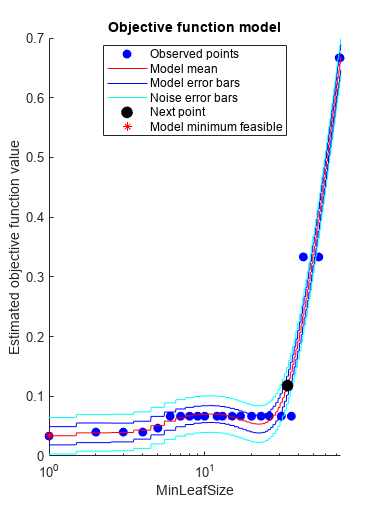
X = meas; Y = species; Mdl = fitctree(X,Y,'OptimizeHyperparameters','auto')
|======================================================================================|
| Iter | Eval | Objective | Objective | BestSoFar | BestSoFar | MinLeafSize |
| | result | | runtime | (observed) | (estim.) | |
|======================================================================================|
| 1 | Best | 0.066667 | 0.96879 | 0.066667 | 0.066667 | 31 |
| 2 | Accept | 0.066667 | 0.48559 | 0.066667 | 0.066667 | 12 |
| 3 | Best | 0.04 | 0.1699 | 0.04 | 0.040003 | 2 |
| 4 | Accept | 0.66667 | 0.21648 | 0.04 | 0.15796 | 73 |
| 5 | Accept | 0.04 | 0.14794 | 0.04 | 0.040009 | 2 |
| 6 | Accept | 0.66667 | 0.15671 | 0.04 | 0.040012 | 74 |
| 7 | Accept | 0.066667 | 0.14561 | 0.04 | 0.040012 | 20 |
| 8 | Accept | 0.04 | 0.11119 | 0.04 | 0.040008 | 4 |
| 9 | Best | 0.033333 | 0.07511 | 0.033333 | 0.03335 | 1 |
| 10 | Accept | 0.066667 | 0.12097 | 0.033333 | 0.03335 | 7 |
| 11 | Accept | 0.04 | 0.11721 | 0.033333 | 0.033348 | 3 |
| 12 | Accept | 0.066667 | 0.072607 | 0.033333 | 0.033348 | 26 |
| 13 | Accept | 0.046667 | 0.081354 | 0.033333 | 0.033347 | 5 |
| 14 | Accept | 0.033333 | 0.075442 | 0.033333 | 0.03334 | 1 |
| 15 | Accept | 0.033333 | 0.15484 | 0.033333 | 0.033337 | 1 |
| 16 | Accept | 0.033333 | 0.2284 | 0.033333 | 0.033336 | 1 |
| 17 | Accept | 0.066667 | 0.12111 | 0.033333 | 0.033336 | 15 |
| 18 | Accept | 0.33333 | 0.23962 | 0.033333 | 0.033336 | 43 |
| 19 | Accept | 0.066667 | 0.08099 | 0.033333 | 0.033336 | 9 |
| 20 | Accept | 0.066667 | 0.2098 | 0.033333 | 0.033336 | 6 |
|======================================================================================|
| Iter | Eval | Objective | Objective | BestSoFar | BestSoFar | MinLeafSize |
| | result | | runtime | (observed) | (estim.) | |
|======================================================================================|
| 21 | Accept | 0.066667 | 0.067257 | 0.033333 | 0.033336 | 17 |
| 22 | Accept | 0.066667 | 0.07785 | 0.033333 | 0.033336 | 10 |
| 23 | Accept | 0.066667 | 0.12608 | 0.033333 | 0.033336 | 36 |
| 24 | Accept | 0.33333 | 0.088971 | 0.033333 | 0.034075 | 54 |
| 25 | Accept | 0.04 | 0.10545 | 0.033333 | 0.034054 | 2 |
| 26 | Accept | 0.04 | 0.21242 | 0.033333 | 0.034022 | 3 |
| 27 | Accept | 0.04 | 0.06971 | 0.033333 | 0.033997 | 4 |
| 28 | Accept | 0.066667 | 0.097256 | 0.033333 | 0.033973 | 23 |
| 29 | Accept | 0.066667 | 0.11986 | 0.033333 | 0.033946 | 8 |
| 30 | Accept | 0.066667 | 0.063491 | 0.033333 | 0.033922 | 13 |
__________________________________________________________
Optimization completed.
MaxObjectiveEvaluations of 30 reached.
Total function evaluations: 30
Total elapsed time: 29.8173 seconds
Total objective function evaluation time: 5.008
Best observed feasible point:
MinLeafSize
___________
1
Observed objective function value = 0.033333
Estimated objective function value = 0.033922
Function evaluation time = 0.07511
Best estimated feasible point (according to models):
MinLeafSize
___________
1
Estimated objective function value = 0.033922
Estimated function evaluation time = 0.13144
Mdl =
ClassificationTree
ResponseName: 'Y'
CategoricalPredictors: []
ClassNames: {'setosa' 'versicolor' 'virginica'}
ScoreTransform: 'none'
NumObservations: 150
HyperparameterOptimizationResults: [1x1 BayesianOptimization]
Unbiased Predictor Importance Estimates
Load the census1994 data set. Consider a model that predicts a person's salary category given their age, working class, education level, martial status, race, sex, capital gain and loss, and number of working hours per week.
load census1994 X = adultdata(:,{'age','workClass','education_num','marital_status','race',... 'sex','capital_gain','capital_loss','hours_per_week','salary'});
Display the number of categories represented in the categorical variables using summary.
summary(X)
Variables:
age: 32561x1 double
Values:
Min 17
Median 37
Max 90
workClass: 32561x1 categorical
Values:
Federal-gov 960
Local-gov 2093
Never-worked 7
Private 22696
Self-emp-inc 1116
Self-emp-not-inc 2541
State-gov 1298
Without-pay 14
NumMissing 1836
education_num: 32561x1 double
Values:
Min 1
Median 10
Max 16
marital_status: 32561x1 categorical
Values:
Divorced 4443
Married-AF-spouse 23
Married-civ-spouse 14976
Married-spouse-absent 418
Never-married 10683
Separated 1025
Widowed 993
race: 32561x1 categorical
Values:
Amer-Indian-Eskimo 311
Asian-Pac-Islander 1039
Black 3124
Other 271
White 27816
sex: 32561x1 categorical
Values:
Female 10771
Male 21790
capital_gain: 32561x1 double
Values:
Min 0
Median 0
Max 99999
capital_loss: 32561x1 double
Values:
Min 0
Median 0
Max 4356
hours_per_week: 32561x1 double
Values:
Min 1
Median 40
Max 99
salary: 32561x1 categorical
Values:
<=50K 24720
>50K 7841
Because there are few categories represented in the categorical variables compared to levels in the continuous variables, the standard CART, predictor-splitting algorithm prefers splitting a continuous predictor over the categorical variables.
Train a classification tree using the entire data set. To grow unbiased trees, specify usage of the curvature test for splitting predictors. Because there are missing observations in the data, specify usage of surrogate splits.
Mdl = fitctree(X,'salary','PredictorSelection','curvature',... 'Surrogate','on');
Estimate predictor importance values by summing changes in the risk due to splits on every predictor and dividing the sum by the number of branch nodes. Compare the estimates using a bar graph.
imp = predictorImportance(Mdl); figure; bar(imp); title('Predictor Importance Estimates'); ylabel('Estimates'); xlabel('Predictors'); h = gca; h.XTickLabel = Mdl.PredictorNames; h.XTickLabelRotation = 45; h.TickLabelInterpreter = 'none';
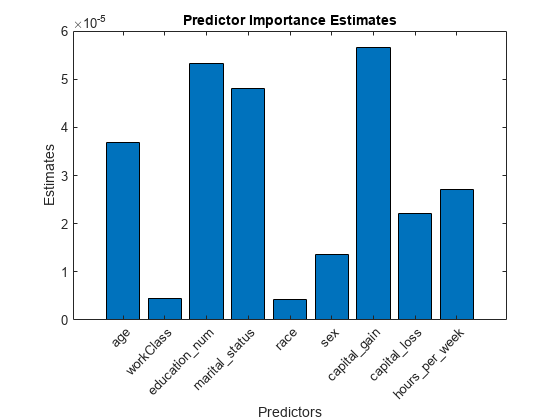
In this case, capital_gain is the most important predictor, followed by education_num.
Optimize Classification Tree on Tall Array
This example shows how to optimize hyperparameters of a classification tree automatically using a tall array. The sample data set airlinesmall.csv is a large data set that contains a tabular file of airline flight data. This example creates a tall table containing the data and uses it to run the optimization procedure.
When you perform calculations on tall arrays, MATLAB® uses either a parallel pool (default if you have Parallel Computing Toolbox™) or the local MATLAB session. If you want to run the example using the local MATLAB session when you have Parallel Computing Toolbox, you can change the global execution environment by using the mapreducer function.
Create a datastore that references the folder location with the data. Select a subset of the variables to work with, and treat 'NA' values as missing data so that datastore replaces them with NaN values. Create a tall table that contains the data in the datastore.
ds = datastore('airlinesmall.csv'); ds.SelectedVariableNames = {'Month','DayofMonth','DayOfWeek',... 'DepTime','ArrDelay','Distance','DepDelay'}; ds.TreatAsMissing = 'NA'; tt = tall(ds) % Tall table
Starting parallel pool (parpool) using the 'local' profile ...
Connected to the parallel pool (number of workers: 6).
tt =
M×7 tall table
Month DayofMonth DayOfWeek DepTime ArrDelay Distance DepDelay
_____ __________ _________ _______ ________ ________ ________
10 21 3 642 8 308 12
10 26 1 1021 8 296 1
10 23 5 2055 21 480 20
10 23 5 1332 13 296 12
10 22 4 629 4 373 -1
10 28 3 1446 59 308 63
10 8 4 928 3 447 -2
10 10 6 859 11 954 -1
: : : : : : :
: : : : : : :
Determine the flights that are late by 10 minutes or more by defining a logical variable that is true for a late flight. This variable contains the class labels. A preview of this variable includes the first few rows.
Y = tt.DepDelay > 10 % Class labelsY = M×1 tall logical array 1 0 1 1 0 1 0 0 : :
Create a tall array for the predictor data.
X = tt{:,1:end-1} % Predictor dataX =
M×6 tall double matrix
10 21 3 642 8 308
10 26 1 1021 8 296
10 23 5 2055 21 480
10 23 5 1332 13 296
10 22 4 629 4 373
10 28 3 1446 59 308
10 8 4 928 3 447
10 10 6 859 11 954
: : : : : :
: : : : : :
Remove rows in X and Y that contain missing data.
R = rmmissing([X Y]); % Data with missing entries removed
X = R(:,1:end-1);
Y = R(:,end); Standardize the predictor variables.
Z = zscore(X);
Optimize hyperparameters automatically using the 'OptimizeHyperparameters' name-value pair argument. Find the optimal 'MinLeafSize' value that minimizes holdout cross-validation loss. (Specifying 'auto' uses 'MinLeafSize'.) For reproducibility, use the 'expected-improvement-plus' acquisition function and set the seeds of the random number generators using rng and tallrng. The results can vary depending on the number of workers and the execution environment for the tall arrays. For details, see Control Where Your Code Runs.
rng('default') tallrng('default') [Mdl,FitInfo,HyperparameterOptimizationResults] = fitctree(Z,Y,... 'OptimizeHyperparameters','auto',... 'HyperparameterOptimizationOptions',struct('Holdout',0.3,... 'AcquisitionFunctionName','expected-improvement-plus'))
Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 3: Completed in 5.6 sec - Pass 2 of 3: Completed in 2.1 sec - Pass 3 of 3: Completed in 3.4 sec Evaluation completed in 13 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.73 sec Evaluation completed in 0.9 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 1.2 sec Evaluation completed in 1.5 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.64 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 0.72 sec - Pass 4 of 4: Completed in 1.1 sec Evaluation completed in 5.9 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.53 sec - Pass 2 of 4: Completed in 0.73 sec - Pass 3 of 4: Completed in 0.58 sec - Pass 4 of 4: Completed in 0.8 sec Evaluation completed in 3.5 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.54 sec - Pass 2 of 4: Completed in 0.72 sec - Pass 3 of 4: Completed in 0.54 sec - Pass 4 of 4: Completed in 0.79 sec Evaluation completed in 3.5 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.51 sec - Pass 2 of 4: Completed in 0.72 sec - Pass 3 of 4: Completed in 0.59 sec - Pass 4 of 4: Completed in 0.87 sec Evaluation completed in 3.3 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.56 sec - Pass 2 of 4: Completed in 0.8 sec - Pass 3 of 4: Completed in 0.54 sec - Pass 4 of 4: Completed in 0.89 sec Evaluation completed in 3.4 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.57 sec - Pass 2 of 4: Completed in 0.74 sec - Pass 3 of 4: Completed in 0.58 sec - Pass 4 of 4: Completed in 1 sec Evaluation completed in 3.5 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.54 sec - Pass 2 of 4: Completed in 1.3 sec - Pass 3 of 4: Completed in 0.68 sec - Pass 4 of 4: Completed in 1.3 sec Evaluation completed in 4.3 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.65 sec - Pass 2 of 4: Completed in 0.73 sec - Pass 3 of 4: Completed in 0.65 sec - Pass 4 of 4: Completed in 1.7 sec Evaluation completed in 4.4 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.63 sec - Pass 2 of 4: Completed in 0.85 sec - Pass 3 of 4: Completed in 0.58 sec - Pass 4 of 4: Completed in 2.2 sec Evaluation completed in 4.9 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 1.2 sec - Pass 2 of 4: Completed in 0.88 sec - Pass 3 of 4: Completed in 0.58 sec - Pass 4 of 4: Completed in 3 sec Evaluation completed in 6.9 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.72 sec - Pass 2 of 4: Completed in 0.96 sec - Pass 3 of 4: Completed in 0.59 sec - Pass 4 of 4: Completed in 4.2 sec Evaluation completed in 7.2 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.77 sec - Pass 2 of 4: Completed in 0.95 sec - Pass 3 of 4: Completed in 0.65 sec - Pass 4 of 4: Completed in 4.8 sec Evaluation completed in 7.9 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.79 sec - Pass 2 of 4: Completed in 1 sec - Pass 3 of 4: Completed in 0.61 sec - Pass 4 of 4: Completed in 5.1 sec Evaluation completed in 8.4 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.89 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 0.59 sec - Pass 4 of 4: Completed in 5.8 sec Evaluation completed in 9.3 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 1 sec - Pass 2 of 4: Completed in 1.2 sec - Pass 3 of 4: Completed in 0.63 sec - Pass 4 of 4: Completed in 5.2 sec Evaluation completed in 8.9 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 1.6 sec - Pass 2 of 4: Completed in 1.3 sec - Pass 3 of 4: Completed in 0.74 sec - Pass 4 of 4: Completed in 4.8 sec Evaluation completed in 9.2 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 1 sec - Pass 2 of 4: Completed in 1.3 sec - Pass 3 of 4: Completed in 0.68 sec - Pass 4 of 4: Completed in 3.9 sec Evaluation completed in 7.7 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 1.6 sec - Pass 2 of 4: Completed in 1.3 sec - Pass 3 of 4: Completed in 0.7 sec - Pass 4 of 4: Completed in 3 sec Evaluation completed in 7.3 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 1.1 sec - Pass 2 of 4: Completed in 1.3 sec - Pass 3 of 4: Completed in 0.66 sec - Pass 4 of 4: Completed in 2.5 sec Evaluation completed in 6.1 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 1.1 sec - Pass 2 of 4: Completed in 1.3 sec - Pass 3 of 4: Completed in 0.66 sec - Pass 4 of 4: Completed in 2.2 sec Evaluation completed in 5.9 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 1.1 sec - Pass 2 of 4: Completed in 1.3 sec - Pass 3 of 4: Completed in 0.69 sec - Pass 4 of 4: Completed in 1.9 sec Evaluation completed in 5.5 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 1.2 sec - Pass 2 of 4: Completed in 1.4 sec - Pass 3 of 4: Completed in 0.67 sec - Pass 4 of 4: Completed in 1.6 sec Evaluation completed in 5.5 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 1.3 sec - Pass 2 of 4: Completed in 1.4 sec - Pass 3 of 4: Completed in 0.65 sec - Pass 4 of 4: Completed in 1.5 sec Evaluation completed in 5.4 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 1.1 sec - Pass 2 of 4: Completed in 1.3 sec - Pass 3 of 4: Completed in 0.67 sec - Pass 4 of 4: Completed in 1.3 sec Evaluation completed in 5 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 1.2 sec - Pass 2 of 4: Completed in 1.3 sec - Pass 3 of 4: Completed in 0.73 sec - Pass 4 of 4: Completed in 1.3 sec Evaluation completed in 5.1 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 1.1 sec - Pass 2 of 4: Completed in 1.3 sec - Pass 3 of 4: Completed in 0.65 sec - Pass 4 of 4: Completed in 1.4 sec Evaluation completed in 5.1 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 2.4 sec Evaluation completed in 2.6 sec |======================================================================================| | Iter | Eval | Objective | Objective | BestSoFar | BestSoFar | MinLeafSize | | | result | | runtime | (observed) | (estim.) | | |======================================================================================| | 1 | Best | 0.11572 | 197.12 | 0.11572 | 0.11572 | 10 | Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.4 sec Evaluation completed in 0.56 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.93 sec Evaluation completed in 1.1 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.5 sec - Pass 2 of 4: Completed in 0.7 sec - Pass 3 of 4: Completed in 1.1 sec - Pass 4 of 4: Completed in 0.84 sec Evaluation completed in 3.7 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 1.4 sec Evaluation completed in 1.6 sec | 2 | Accept | 0.19635 | 10.496 | 0.11572 | 0.12008 | 48298 | Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.33 sec Evaluation completed in 0.47 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.83 sec Evaluation completed in 0.99 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.49 sec - Pass 2 of 4: Completed in 0.68 sec - Pass 3 of 4: Completed in 0.52 sec - Pass 4 of 4: Completed in 0.74 sec Evaluation completed in 3 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.48 sec - Pass 2 of 4: Completed in 0.69 sec - Pass 3 of 4: Completed in 0.51 sec - Pass 4 of 4: Completed in 0.73 sec Evaluation completed in 3 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.51 sec - Pass 2 of 4: Completed in 0.71 sec - Pass 3 of 4: Completed in 0.68 sec - Pass 4 of 4: Completed in 0.77 sec Evaluation completed in 3.2 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.48 sec - Pass 2 of 4: Completed in 0.7 sec - Pass 3 of 4: Completed in 0.55 sec - Pass 4 of 4: Completed in 0.86 sec Evaluation completed in 3.1 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.5 sec - Pass 2 of 4: Completed in 0.69 sec - Pass 3 of 4: Completed in 0.55 sec - Pass 4 of 4: Completed in 0.76 sec Evaluation completed in 3.1 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.52 sec - Pass 2 of 4: Completed in 0.7 sec - Pass 3 of 4: Completed in 0.5 sec - Pass 4 of 4: Completed in 0.76 sec Evaluation completed in 3 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.54 sec - Pass 2 of 4: Completed in 0.75 sec - Pass 3 of 4: Completed in 0.55 sec - Pass 4 of 4: Completed in 1.3 sec Evaluation completed in 4 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.53 sec - Pass 2 of 4: Completed in 0.74 sec - Pass 3 of 4: Completed in 0.55 sec - Pass 4 of 4: Completed in 0.78 sec Evaluation completed in 3.1 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.56 sec - Pass 2 of 4: Completed in 0.76 sec - Pass 3 of 4: Completed in 0.56 sec - Pass 4 of 4: Completed in 0.78 sec Evaluation completed in 3.2 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.75 sec Evaluation completed in 0.87 sec | 3 | Best | 0.1048 | 44.614 | 0.1048 | 0.11431 | 3166 | Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.3 sec Evaluation completed in 0.45 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.83 sec Evaluation completed in 0.97 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.99 sec - Pass 2 of 4: Completed in 0.68 sec - Pass 3 of 4: Completed in 0.52 sec - Pass 4 of 4: Completed in 0.73 sec Evaluation completed in 3.5 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.47 sec - Pass 2 of 4: Completed in 0.76 sec - Pass 3 of 4: Completed in 0.54 sec - Pass 4 of 4: Completed in 0.82 sec Evaluation completed in 3.2 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.52 sec - Pass 2 of 4: Completed in 0.74 sec - Pass 3 of 4: Completed in 0.54 sec - Pass 4 of 4: Completed in 0.81 sec Evaluation completed in 3.2 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.55 sec - Pass 2 of 4: Completed in 0.7 sec - Pass 3 of 4: Completed in 0.53 sec - Pass 4 of 4: Completed in 0.81 sec Evaluation completed in 3.1 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.52 sec - Pass 2 of 4: Completed in 0.77 sec - Pass 3 of 4: Completed in 0.58 sec - Pass 4 of 4: Completed in 0.89 sec Evaluation completed in 3.3 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.51 sec - Pass 2 of 4: Completed in 0.74 sec - Pass 3 of 4: Completed in 0.6 sec - Pass 4 of 4: Completed in 1.5 sec Evaluation completed in 3.9 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 1 sec - Pass 2 of 4: Completed in 0.75 sec - Pass 3 of 4: Completed in 0.55 sec - Pass 4 of 4: Completed in 1.1 sec Evaluation completed in 4.1 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.52 sec - Pass 2 of 4: Completed in 0.78 sec - Pass 3 of 4: Completed in 0.5 sec - Pass 4 of 4: Completed in 1.3 sec Evaluation completed in 3.6 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.63 sec - Pass 2 of 4: Completed in 1.3 sec - Pass 3 of 4: Completed in 0.61 sec - Pass 4 of 4: Completed in 1.4 sec Evaluation completed in 4.5 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.59 sec - Pass 2 of 4: Completed in 0.8 sec - Pass 3 of 4: Completed in 0.57 sec - Pass 4 of 4: Completed in 1.5 sec Evaluation completed in 4.1 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.66 sec - Pass 2 of 4: Completed in 0.81 sec - Pass 3 of 4: Completed in 0.52 sec - Pass 4 of 4: Completed in 1.5 sec Evaluation completed in 4.2 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.62 sec - Pass 2 of 4: Completed in 0.75 sec - Pass 3 of 4: Completed in 0.61 sec - Pass 4 of 4: Completed in 1.4 sec Evaluation completed in 3.9 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.61 sec - Pass 2 of 4: Completed in 0.78 sec - Pass 3 of 4: Completed in 1.1 sec - Pass 4 of 4: Completed in 1.6 sec Evaluation completed in 4.7 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.6 sec - Pass 2 of 4: Completed in 0.81 sec - Pass 3 of 4: Completed in 0.55 sec - Pass 4 of 4: Completed in 1.5 sec Evaluation completed in 4 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.61 sec - Pass 2 of 4: Completed in 0.78 sec - Pass 3 of 4: Completed in 0.55 sec - Pass 4 of 4: Completed in 0.9 sec Evaluation completed in 3.4 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.59 sec - Pass 2 of 4: Completed in 0.81 sec - Pass 3 of 4: Completed in 0.53 sec - Pass 4 of 4: Completed in 0.81 sec Evaluation completed in 3.3 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.59 sec - Pass 2 of 4: Completed in 0.78 sec - Pass 3 of 4: Completed in 1 sec - Pass 4 of 4: Completed in 1.3 sec Evaluation completed in 4.3 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.8 sec Evaluation completed in 0.94 sec | 4 | Best | 0.10094 | 91.723 | 0.10094 | 0.10574 | 180 | Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.3 sec Evaluation completed in 0.42 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.93 sec Evaluation completed in 1.1 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.55 sec - Pass 2 of 4: Completed in 0.66 sec - Pass 3 of 4: Completed in 0.55 sec - Pass 4 of 4: Completed in 0.83 sec Evaluation completed in 3.1 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.49 sec - Pass 2 of 4: Completed in 0.71 sec - Pass 3 of 4: Completed in 0.54 sec - Pass 4 of 4: Completed in 0.76 sec Evaluation completed in 3.1 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.5 sec - Pass 2 of 4: Completed in 0.7 sec - Pass 3 of 4: Completed in 0.56 sec - Pass 4 of 4: Completed in 0.78 sec Evaluation completed in 3.1 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.56 sec - Pass 2 of 4: Completed in 0.72 sec - Pass 3 of 4: Completed in 0.51 sec - Pass 4 of 4: Completed in 0.81 sec Evaluation completed in 3.2 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.52 sec - Pass 2 of 4: Completed in 1.3 sec - Pass 3 of 4: Completed in 1.1 sec - Pass 4 of 4: Completed in 0.88 sec Evaluation completed in 4.3 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.52 sec - Pass 2 of 4: Completed in 0.7 sec - Pass 3 of 4: Completed in 0.5 sec - Pass 4 of 4: Completed in 0.98 sec Evaluation completed in 3.3 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.56 sec - Pass 2 of 4: Completed in 0.74 sec - Pass 3 of 4: Completed in 0.5 sec - Pass 4 of 4: Completed in 1.1 sec Evaluation completed in 3.5 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.61 sec - Pass 2 of 4: Completed in 0.81 sec - Pass 3 of 4: Completed in 0.56 sec - Pass 4 of 4: Completed in 1.2 sec Evaluation completed in 3.8 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.59 sec - Pass 2 of 4: Completed in 0.81 sec - Pass 3 of 4: Completed in 0.7 sec - Pass 4 of 4: Completed in 1.4 sec Evaluation completed in 4.1 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.56 sec - Pass 2 of 4: Completed in 0.73 sec - Pass 3 of 4: Completed in 0.59 sec - Pass 4 of 4: Completed in 1.4 sec Evaluation completed in 3.8 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.58 sec - Pass 2 of 4: Completed in 0.8 sec - Pass 3 of 4: Completed in 0.52 sec - Pass 4 of 4: Completed in 1.2 sec Evaluation completed in 3.7 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.64 sec - Pass 2 of 4: Completed in 0.79 sec - Pass 3 of 4: Completed in 0.54 sec - Pass 4 of 4: Completed in 1.1 sec Evaluation completed in 3.6 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.57 sec - Pass 2 of 4: Completed in 0.78 sec - Pass 3 of 4: Completed in 0.56 sec - Pass 4 of 4: Completed in 0.97 sec Evaluation completed in 3.5 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.55 sec - Pass 2 of 4: Completed in 0.75 sec - Pass 3 of 4: Completed in 0.55 sec - Pass 4 of 4: Completed in 0.89 sec Evaluation completed in 3.3 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.6 sec - Pass 2 of 4: Completed in 1.3 sec - Pass 3 of 4: Completed in 0.61 sec - Pass 4 of 4: Completed in 0.85 sec Evaluation completed in 3.9 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.6 sec - Pass 2 of 4: Completed in 0.82 sec - Pass 3 of 4: Completed in 0.56 sec - Pass 4 of 4: Completed in 0.79 sec Evaluation completed in 3.4 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 1.3 sec Evaluation completed in 1.4 sec | 5 | Best | 0.10087 | 82.84 | 0.10087 | 0.10085 | 219 | Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.32 sec Evaluation completed in 0.45 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.87 sec Evaluation completed in 1 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.5 sec - Pass 2 of 4: Completed in 0.7 sec - Pass 3 of 4: Completed in 0.56 sec - Pass 4 of 4: Completed in 0.76 sec Evaluation completed in 3.1 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.53 sec - Pass 2 of 4: Completed in 0.74 sec - Pass 3 of 4: Completed in 0.54 sec - Pass 4 of 4: Completed in 0.79 sec Evaluation completed in 3.2 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.49 sec - Pass 2 of 4: Completed in 0.66 sec - Pass 3 of 4: Completed in 0.5 sec - Pass 4 of 4: Completed in 0.78 sec Evaluation completed in 3 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.49 sec - Pass 2 of 4: Completed in 0.68 sec - Pass 3 of 4: Completed in 0.51 sec - Pass 4 of 4: Completed in 0.81 sec Evaluation completed in 3.1 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.55 sec - Pass 2 of 4: Completed in 0.68 sec - Pass 3 of 4: Completed in 0.54 sec - Pass 4 of 4: Completed in 0.86 sec Evaluation completed in 3.2 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.51 sec - Pass 2 of 4: Completed in 0.71 sec - Pass 3 of 4: Completed in 0.53 sec - Pass 4 of 4: Completed in 1 sec Evaluation completed in 3.4 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.59 sec - Pass 2 of 4: Completed in 1.2 sec - Pass 3 of 4: Completed in 0.55 sec - Pass 4 of 4: Completed in 0.85 sec Evaluation completed in 3.8 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.6 sec - Pass 2 of 4: Completed in 0.74 sec - Pass 3 of 4: Completed in 0.6 sec - Pass 4 of 4: Completed in 0.84 sec Evaluation completed in 3.3 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.51 sec - Pass 2 of 4: Completed in 0.77 sec - Pass 3 of 4: Completed in 0.58 sec - Pass 4 of 4: Completed in 0.87 sec Evaluation completed in 3.3 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.53 sec - Pass 2 of 4: Completed in 0.78 sec - Pass 3 of 4: Completed in 1.1 sec - Pass 4 of 4: Completed in 0.92 sec Evaluation completed in 3.9 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.54 sec - Pass 2 of 4: Completed in 0.81 sec - Pass 3 of 4: Completed in 0.59 sec - Pass 4 of 4: Completed in 0.77 sec Evaluation completed in 3.2 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.53 sec - Pass 2 of 4: Completed in 1.2 sec - Pass 3 of 4: Completed in 0.68 sec - Pass 4 of 4: Completed in 0.86 sec Evaluation completed in 3.9 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.77 sec Evaluation completed in 0.93 sec | 6 | Accept | 0.10155 | 61.043 | 0.10087 | 0.10089 | 1089 | Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.33 sec Evaluation completed in 0.46 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.89 sec Evaluation completed in 1 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.56 sec - Pass 2 of 4: Completed in 0.72 sec - Pass 3 of 4: Completed in 0.56 sec - Pass 4 of 4: Completed in 0.8 sec Evaluation completed in 3.2 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.53 sec - Pass 2 of 4: Completed in 0.69 sec - Pass 3 of 4: Completed in 0.54 sec - Pass 4 of 4: Completed in 0.85 sec Evaluation completed in 3.1 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.51 sec - Pass 2 of 4: Completed in 1.2 sec - Pass 3 of 4: Completed in 0.59 sec - Pass 4 of 4: Completed in 0.83 sec Evaluation completed in 3.8 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 1 sec - Pass 2 of 4: Completed in 0.76 sec - Pass 3 of 4: Completed in 0.56 sec - Pass 4 of 4: Completed in 0.87 sec Evaluation completed in 4 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 1 sec - Pass 2 of 4: Completed in 0.77 sec - Pass 3 of 4: Completed in 0.53 sec - Pass 4 of 4: Completed in 0.9 sec Evaluation completed in 3.8 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 1 sec - Pass 2 of 4: Completed in 0.77 sec - Pass 3 of 4: Completed in 0.51 sec - Pass 4 of 4: Completed in 0.98 sec Evaluation completed in 3.9 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 1 sec - Pass 2 of 4: Completed in 0.78 sec - Pass 3 of 4: Completed in 0.62 sec - Pass 4 of 4: Completed in 1.1 sec Evaluation completed in 4.2 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.52 sec - Pass 2 of 4: Completed in 0.71 sec - Pass 3 of 4: Completed in 0.53 sec - Pass 4 of 4: Completed in 1.5 sec Evaluation completed in 3.9 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.59 sec - Pass 2 of 4: Completed in 0.72 sec - Pass 3 of 4: Completed in 0.59 sec - Pass 4 of 4: Completed in 2 sec Evaluation completed in 4.5 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.59 sec - Pass 2 of 4: Completed in 0.81 sec - Pass 3 of 4: Completed in 0.57 sec - Pass 4 of 4: Completed in 2.7 sec Evaluation completed in 5.4 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.64 sec - Pass 2 of 4: Completed in 0.87 sec - Pass 3 of 4: Completed in 1.2 sec - Pass 4 of 4: Completed in 3.7 sec Evaluation completed in 7.1 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.73 sec - Pass 2 of 4: Completed in 0.92 sec - Pass 3 of 4: Completed in 0.6 sec - Pass 4 of 4: Completed in 4.4 sec Evaluation completed in 7.3 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.86 sec - Pass 2 of 4: Completed in 1.5 sec - Pass 3 of 4: Completed in 0.64 sec - Pass 4 of 4: Completed in 4.8 sec Evaluation completed in 8.6 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.9 sec - Pass 2 of 4: Completed in 1.1 sec - Pass 3 of 4: Completed in 0.65 sec - Pass 4 of 4: Completed in 5.2 sec Evaluation completed in 8.5 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 1 sec - Pass 2 of 4: Completed in 1.3 sec - Pass 3 of 4: Completed in 0.73 sec - Pass 4 of 4: Completed in 5.6 sec Evaluation completed in 9.4 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 1.5 sec - Pass 2 of 4: Completed in 1.6 sec - Pass 3 of 4: Completed in 0.75 sec - Pass 4 of 4: Completed in 5.8 sec Evaluation completed in 10 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 1.3 sec - Pass 2 of 4: Completed in 1.4 sec - Pass 3 of 4: Completed in 1.2 sec - Pass 4 of 4: Completed in 5.1 sec Evaluation completed in 9.9 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 1.4 sec - Pass 2 of 4: Completed in 1.5 sec - Pass 3 of 4: Completed in 0.7 sec - Pass 4 of 4: Completed in 4.1 sec Evaluation completed in 8.5 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 1.4 sec - Pass 2 of 4: Completed in 1.6 sec - Pass 3 of 4: Completed in 0.71 sec - Pass 4 of 4: Completed in 3.6 sec Evaluation completed in 7.9 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 1.5 sec - Pass 2 of 4: Completed in 1.8 sec - Pass 3 of 4: Completed in 0.74 sec - Pass 4 of 4: Completed in 3.2 sec Evaluation completed in 7.9 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 1.4 sec - Pass 2 of 4: Completed in 1.7 sec - Pass 3 of 4: Completed in 0.73 sec - Pass 4 of 4: Completed in 2.8 sec Evaluation completed in 7.3 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 1.5 sec - Pass 2 of 4: Completed in 1.7 sec - Pass 3 of 4: Completed in 0.82 sec - Pass 4 of 4: Completed in 2.4 sec Evaluation completed in 7 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 2 sec - Pass 2 of 4: Completed in 1.9 sec - Pass 3 of 4: Completed in 0.79 sec - Pass 4 of 4: Completed in 2.3 sec Evaluation completed in 7.6 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 1.6 sec - Pass 2 of 4: Completed in 1.8 sec - Pass 3 of 4: Completed in 0.73 sec - Pass 4 of 4: Completed in 2.2 sec Evaluation completed in 6.9 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 1.6 sec - Pass 2 of 4: Completed in 1.7 sec - Pass 3 of 4: Completed in 0.79 sec - Pass 4 of 4: Completed in 2.3 sec Evaluation completed in 7 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 1.7 sec - Pass 2 of 4: Completed in 1.9 sec - Pass 3 of 4: Completed in 0.8 sec - Pass 4 of 4: Completed in 1.8 sec Evaluation completed in 6.8 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 1.7 sec - Pass 2 of 4: Completed in 1.8 sec - Pass 3 of 4: Completed in 0.77 sec - Pass 4 of 4: Completed in 1.8 sec Evaluation completed in 6.6 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 1.4 sec - Pass 2 of 4: Completed in 1.6 sec - Pass 3 of 4: Completed in 0.73 sec - Pass 4 of 4: Completed in 1.8 sec Evaluation completed in 6.1 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 1.5 sec - Pass 2 of 4: Completed in 1.7 sec - Pass 3 of 4: Completed in 1.3 sec - Pass 4 of 4: Completed in 1.7 sec Evaluation completed in 6.7 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 1.5 sec - Pass 2 of 4: Completed in 1.7 sec - Pass 3 of 4: Completed in 0.73 sec - Pass 4 of 4: Completed in 1.8 sec Evaluation completed in 6.3 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 1.3 sec Evaluation completed in 1.5 sec | 7 | Accept | 0.13495 | 241.76 | 0.10087 | 0.10089 | 1 | Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.31 sec Evaluation completed in 0.44 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.87 sec Evaluation completed in 1 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.47 sec - Pass 2 of 4: Completed in 0.67 sec - Pass 3 of 4: Completed in 0.54 sec - Pass 4 of 4: Completed in 0.74 sec Evaluation completed in 3 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.51 sec - Pass 2 of 4: Completed in 0.79 sec - Pass 3 of 4: Completed in 0.56 sec - Pass 4 of 4: Completed in 0.76 sec Evaluation completed in 3.2 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.49 sec - Pass 2 of 4: Completed in 0.69 sec - Pass 3 of 4: Completed in 1.1 sec - Pass 4 of 4: Completed in 0.78 sec Evaluation completed in 3.6 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 1 sec - Pass 2 of 4: Completed in 0.78 sec - Pass 3 of 4: Completed in 0.53 sec - Pass 4 of 4: Completed in 0.85 sec Evaluation completed in 3.8 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.54 sec - Pass 2 of 4: Completed in 0.77 sec - Pass 3 of 4: Completed in 0.52 sec - Pass 4 of 4: Completed in 0.89 sec Evaluation completed in 3.3 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.51 sec - Pass 2 of 4: Completed in 0.73 sec - Pass 3 of 4: Completed in 0.6 sec - Pass 4 of 4: Completed in 1.1 sec Evaluation completed in 3.5 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.53 sec - Pass 2 of 4: Completed in 0.77 sec - Pass 3 of 4: Completed in 0.54 sec - Pass 4 of 4: Completed in 1.3 sec Evaluation completed in 3.7 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.62 sec - Pass 2 of 4: Completed in 0.8 sec - Pass 3 of 4: Completed in 0.61 sec - Pass 4 of 4: Completed in 1.6 sec Evaluation completed in 4.4 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 1.2 sec - Pass 2 of 4: Completed in 1.5 sec - Pass 3 of 4: Completed in 1.1 sec - Pass 4 of 4: Completed in 1.9 sec Evaluation completed in 6.3 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.69 sec - Pass 2 of 4: Completed in 0.88 sec - Pass 3 of 4: Completed in 0.75 sec - Pass 4 of 4: Completed in 2.1 sec Evaluation completed in 5.1 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.61 sec - Pass 2 of 4: Completed in 0.79 sec - Pass 3 of 4: Completed in 0.54 sec - Pass 4 of 4: Completed in 2.2 sec Evaluation completed in 4.8 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.61 sec - Pass 2 of 4: Completed in 0.84 sec - Pass 3 of 4: Completed in 0.58 sec - Pass 4 of 4: Completed in 2.2 sec Evaluation completed in 4.9 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.68 sec - Pass 2 of 4: Completed in 0.85 sec - Pass 3 of 4: Completed in 0.59 sec - Pass 4 of 4: Completed in 2.2 sec Evaluation completed in 4.9 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.68 sec - Pass 2 of 4: Completed in 0.91 sec - Pass 3 of 4: Completed in 0.58 sec - Pass 4 of 4: Completed in 2.4 sec Evaluation completed in 5.3 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.92 sec - Pass 2 of 4: Completed in 0.86 sec - Pass 3 of 4: Completed in 0.57 sec - Pass 4 of 4: Completed in 1.6 sec Evaluation completed in 4.7 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.69 sec - Pass 2 of 4: Completed in 0.91 sec - Pass 3 of 4: Completed in 0.63 sec - Pass 4 of 4: Completed in 1.3 sec Evaluation completed in 4.1 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.67 sec - Pass 2 of 4: Completed in 0.86 sec - Pass 3 of 4: Completed in 0.56 sec - Pass 4 of 4: Completed in 0.99 sec Evaluation completed in 3.6 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 1.2 sec - Pass 2 of 4: Completed in 0.9 sec - Pass 3 of 4: Completed in 0.57 sec - Pass 4 of 4: Completed in 0.95 sec Evaluation completed in 4.2 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.73 sec - Pass 2 of 4: Completed in 0.91 sec - Pass 3 of 4: Completed in 0.57 sec - Pass 4 of 4: Completed in 0.91 sec Evaluation completed in 3.7 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.76 sec - Pass 2 of 4: Completed in 0.93 sec - Pass 3 of 4: Completed in 0.57 sec - Pass 4 of 4: Completed in 0.9 sec Evaluation completed in 3.7 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.91 sec Evaluation completed in 1.1 sec | 8 | Accept | 0.10246 | 115.31 | 0.10087 | 0.10089 | 58 | Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.34 sec Evaluation completed in 0.49 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.87 sec Evaluation completed in 1 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.55 sec - Pass 2 of 4: Completed in 0.72 sec - Pass 3 of 4: Completed in 0.57 sec - Pass 4 of 4: Completed in 0.8 sec Evaluation completed in 3.2 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.48 sec - Pass 2 of 4: Completed in 0.7 sec - Pass 3 of 4: Completed in 0.52 sec - Pass 4 of 4: Completed in 0.76 sec Evaluation completed in 3 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.51 sec - Pass 2 of 4: Completed in 0.69 sec - Pass 3 of 4: Completed in 0.54 sec - Pass 4 of 4: Completed in 0.79 sec Evaluation completed in 3.1 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.53 sec - Pass 2 of 4: Completed in 0.72 sec - Pass 3 of 4: Completed in 0.56 sec - Pass 4 of 4: Completed in 0.81 sec Evaluation completed in 3.2 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 1 sec - Pass 2 of 4: Completed in 0.75 sec - Pass 3 of 4: Completed in 0.56 sec - Pass 4 of 4: Completed in 1.4 sec Evaluation completed in 4.3 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.55 sec - Pass 2 of 4: Completed in 0.77 sec - Pass 3 of 4: Completed in 0.6 sec - Pass 4 of 4: Completed in 0.9 sec Evaluation completed in 3.3 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.5 sec - Pass 2 of 4: Completed in 0.73 sec - Pass 3 of 4: Completed in 1.1 sec - Pass 4 of 4: Completed in 1.1 sec Evaluation completed in 4 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.56 sec - Pass 2 of 4: Completed in 0.75 sec - Pass 3 of 4: Completed in 0.53 sec - Pass 4 of 4: Completed in 1.2 sec Evaluation completed in 3.5 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.61 sec - Pass 2 of 4: Completed in 0.76 sec - Pass 3 of 4: Completed in 1.1 sec - Pass 4 of 4: Completed in 1.1 sec Evaluation completed in 4.1 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.6 sec - Pass 2 of 4: Completed in 0.74 sec - Pass 3 of 4: Completed in 0.53 sec - Pass 4 of 4: Completed in 0.95 sec Evaluation completed in 3.4 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.55 sec - Pass 2 of 4: Completed in 0.76 sec - Pass 3 of 4: Completed in 0.57 sec - Pass 4 of 4: Completed in 0.94 sec Evaluation completed in 3.4 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.58 sec - Pass 2 of 4: Completed in 0.77 sec - Pass 3 of 4: Completed in 0.54 sec - Pass 4 of 4: Completed in 0.83 sec Evaluation completed in 3.3 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.59 sec - Pass 2 of 4: Completed in 0.78 sec - Pass 3 of 4: Completed in 0.57 sec - Pass 4 of 4: Completed in 0.83 sec Evaluation completed in 3.4 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.6 sec - Pass 2 of 4: Completed in 0.76 sec - Pass 3 of 4: Completed in 0.55 sec - Pass 4 of 4: Completed in 0.77 sec Evaluation completed in 3.3 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.72 sec - Pass 2 of 4: Completed in 0.81 sec - Pass 3 of 4: Completed in 0.6 sec - Pass 4 of 4: Completed in 0.76 sec Evaluation completed in 3.6 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 1.3 sec Evaluation completed in 1.4 sec | 9 | Accept | 0.10173 | 77.229 | 0.10087 | 0.10086 | 418 | Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.32 sec Evaluation completed in 0.46 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.84 sec Evaluation completed in 1 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.5 sec - Pass 2 of 4: Completed in 0.72 sec - Pass 3 of 4: Completed in 0.57 sec - Pass 4 of 4: Completed in 0.75 sec Evaluation completed in 3.1 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.49 sec - Pass 2 of 4: Completed in 0.68 sec - Pass 3 of 4: Completed in 0.55 sec - Pass 4 of 4: Completed in 0.76 sec Evaluation completed in 3 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.52 sec - Pass 2 of 4: Completed in 0.71 sec - Pass 3 of 4: Completed in 0.54 sec - Pass 4 of 4: Completed in 0.91 sec Evaluation completed in 3.3 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.53 sec - Pass 2 of 4: Completed in 0.69 sec - Pass 3 of 4: Completed in 0.52 sec - Pass 4 of 4: Completed in 0.82 sec Evaluation completed in 3.1 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.51 sec - Pass 2 of 4: Completed in 0.7 sec - Pass 3 of 4: Completed in 0.61 sec - Pass 4 of 4: Completed in 0.82 sec Evaluation completed in 3.2 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 1.1 sec - Pass 2 of 4: Completed in 0.78 sec - Pass 3 of 4: Completed in 0.54 sec - Pass 4 of 4: Completed in 0.95 sec Evaluation completed in 3.9 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.55 sec - Pass 2 of 4: Completed in 0.71 sec - Pass 3 of 4: Completed in 0.53 sec - Pass 4 of 4: Completed in 1.1 sec Evaluation completed in 3.5 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.54 sec - Pass 2 of 4: Completed in 0.7 sec - Pass 3 of 4: Completed in 0.58 sec - Pass 4 of 4: Completed in 1.3 sec Evaluation completed in 3.7 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.55 sec - Pass 2 of 4: Completed in 0.73 sec - Pass 3 of 4: Completed in 0.59 sec - Pass 4 of 4: Completed in 1.7 sec Evaluation completed in 4.2 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.58 sec - Pass 2 of 4: Completed in 0.79 sec - Pass 3 of 4: Completed in 0.56 sec - Pass 4 of 4: Completed in 1.7 sec Evaluation completed in 4.2 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.71 sec - Pass 2 of 4: Completed in 1.7 sec - Pass 3 of 4: Completed in 0.59 sec - Pass 4 of 4: Completed in 1.7 sec Evaluation completed in 5.2 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.65 sec - Pass 2 of 4: Completed in 0.83 sec - Pass 3 of 4: Completed in 0.61 sec - Pass 4 of 4: Completed in 1.4 sec Evaluation completed in 4.1 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.67 sec - Pass 2 of 4: Completed in 0.87 sec - Pass 3 of 4: Completed in 0.58 sec - Pass 4 of 4: Completed in 1.4 sec Evaluation completed in 4.1 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.61 sec - Pass 2 of 4: Completed in 0.82 sec - Pass 3 of 4: Completed in 0.55 sec - Pass 4 of 4: Completed in 1.1 sec Evaluation completed in 3.7 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.65 sec - Pass 2 of 4: Completed in 0.84 sec - Pass 3 of 4: Completed in 0.62 sec - Pass 4 of 4: Completed in 0.89 sec Evaluation completed in 3.6 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.64 sec - Pass 2 of 4: Completed in 0.81 sec - Pass 3 of 4: Completed in 0.56 sec - Pass 4 of 4: Completed in 0.88 sec Evaluation completed in 3.6 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.62 sec - Pass 2 of 4: Completed in 0.9 sec - Pass 3 of 4: Completed in 0.55 sec - Pass 4 of 4: Completed in 0.86 sec Evaluation completed in 3.5 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.65 sec - Pass 2 of 4: Completed in 0.81 sec - Pass 3 of 4: Completed in 0.56 sec - Pass 4 of 4: Completed in 0.8 sec Evaluation completed in 3.3 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.77 sec Evaluation completed in 0.89 sec | 10 | Accept | 0.10114 | 94.532 | 0.10087 | 0.10091 | 123 | Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.86 sec Evaluation completed in 1 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.83 sec Evaluation completed in 0.99 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.48 sec - Pass 2 of 4: Completed in 0.7 sec - Pass 3 of 4: Completed in 0.54 sec - Pass 4 of 4: Completed in 0.8 sec Evaluation completed in 3 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.5 sec - Pass 2 of 4: Completed in 0.72 sec - Pass 3 of 4: Completed in 0.53 sec - Pass 4 of 4: Completed in 0.79 sec Evaluation completed in 3.1 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.56 sec - Pass 2 of 4: Completed in 0.73 sec - Pass 3 of 4: Completed in 0.54 sec - Pass 4 of 4: Completed in 0.85 sec Evaluation completed in 3.3 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.5 sec - Pass 2 of 4: Completed in 0.69 sec - Pass 3 of 4: Completed in 0.55 sec - Pass 4 of 4: Completed in 0.81 sec Evaluation completed in 3.2 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.55 sec - Pass 2 of 4: Completed in 0.82 sec - Pass 3 of 4: Completed in 0.64 sec - Pass 4 of 4: Completed in 0.94 sec Evaluation completed in 3.5 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.49 sec - Pass 2 of 4: Completed in 0.77 sec - Pass 3 of 4: Completed in 0.53 sec - Pass 4 of 4: Completed in 0.97 sec Evaluation completed in 3.3 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.56 sec - Pass 2 of 4: Completed in 0.78 sec - Pass 3 of 4: Completed in 0.58 sec - Pass 4 of 4: Completed in 1.3 sec Evaluation completed in 3.8 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.55 sec - Pass 2 of 4: Completed in 0.81 sec - Pass 3 of 4: Completed in 0.56 sec - Pass 4 of 4: Completed in 1.3 sec Evaluation completed in 3.8 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.55 sec - Pass 2 of 4: Completed in 0.76 sec - Pass 3 of 4: Completed in 0.56 sec - Pass 4 of 4: Completed in 1.5 sec Evaluation completed in 3.9 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.59 sec - Pass 2 of 4: Completed in 0.76 sec - Pass 3 of 4: Completed in 0.55 sec - Pass 4 of 4: Completed in 1.5 sec Evaluation completed in 4 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.59 sec - Pass 2 of 4: Completed in 0.8 sec - Pass 3 of 4: Completed in 0.59 sec - Pass 4 of 4: Completed in 1.4 sec Evaluation completed in 3.9 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.59 sec - Pass 2 of 4: Completed in 0.77 sec - Pass 3 of 4: Completed in 0.55 sec - Pass 4 of 4: Completed in 1.2 sec Evaluation completed in 3.7 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 1.1 sec - Pass 2 of 4: Completed in 0.8 sec - Pass 3 of 4: Completed in 0.58 sec - Pass 4 of 4: Completed in 1.1 sec Evaluation completed in 4.2 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.65 sec - Pass 2 of 4: Completed in 0.84 sec - Pass 3 of 4: Completed in 1.1 sec - Pass 4 of 4: Completed in 1 sec Evaluation completed in 4.3 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.63 sec - Pass 2 of 4: Completed in 0.84 sec - Pass 3 of 4: Completed in 0.59 sec - Pass 4 of 4: Completed in 0.9 sec Evaluation completed in 3.5 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 1.2 sec - Pass 2 of 4: Completed in 0.83 sec - Pass 3 of 4: Completed in 0.56 sec - Pass 4 of 4: Completed in 0.81 sec Evaluation completed in 4 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.65 sec - Pass 2 of 4: Completed in 0.79 sec - Pass 3 of 4: Completed in 0.59 sec - Pass 4 of 4: Completed in 0.8 sec Evaluation completed in 3.4 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.77 sec Evaluation completed in 0.89 sec | 11 | Best | 0.1008 | 90.637 | 0.1008 | 0.10088 | 178 | Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.38 sec Evaluation completed in 0.52 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.88 sec Evaluation completed in 1 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.49 sec - Pass 2 of 4: Completed in 0.69 sec - Pass 3 of 4: Completed in 0.51 sec - Pass 4 of 4: Completed in 0.78 sec Evaluation completed in 3 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.59 sec - Pass 2 of 4: Completed in 0.72 sec - Pass 3 of 4: Completed in 0.53 sec - Pass 4 of 4: Completed in 0.79 sec Evaluation completed in 3.1 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.58 sec - Pass 2 of 4: Completed in 0.74 sec - Pass 3 of 4: Completed in 0.55 sec - Pass 4 of 4: Completed in 0.93 sec Evaluation completed in 3.4 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.57 sec - Pass 2 of 4: Completed in 0.79 sec - Pass 3 of 4: Completed in 0.58 sec - Pass 4 of 4: Completed in 0.83 sec Evaluation completed in 3.3 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.53 sec - Pass 2 of 4: Completed in 1.2 sec - Pass 3 of 4: Completed in 0.59 sec - Pass 4 of 4: Completed in 0.91 sec Evaluation completed in 3.8 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.58 sec - Pass 2 of 4: Completed in 0.85 sec - Pass 3 of 4: Completed in 0.58 sec - Pass 4 of 4: Completed in 1 sec Evaluation completed in 3.6 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.56 sec - Pass 2 of 4: Completed in 0.77 sec - Pass 3 of 4: Completed in 0.55 sec - Pass 4 of 4: Completed in 1.2 sec Evaluation completed in 3.6 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 1.1 sec - Pass 2 of 4: Completed in 0.81 sec - Pass 3 of 4: Completed in 0.52 sec - Pass 4 of 4: Completed in 1.4 sec Evaluation completed in 4.4 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.54 sec - Pass 2 of 4: Completed in 0.74 sec - Pass 3 of 4: Completed in 0.54 sec - Pass 4 of 4: Completed in 1.5 sec Evaluation completed in 3.9 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.61 sec - Pass 2 of 4: Completed in 0.79 sec - Pass 3 of 4: Completed in 0.58 sec - Pass 4 of 4: Completed in 1.5 sec Evaluation completed in 4 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.61 sec - Pass 2 of 4: Completed in 0.82 sec - Pass 3 of 4: Completed in 0.61 sec - Pass 4 of 4: Completed in 1.4 sec Evaluation completed in 4 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.66 sec - Pass 2 of 4: Completed in 0.77 sec - Pass 3 of 4: Completed in 0.54 sec - Pass 4 of 4: Completed in 1.2 sec Evaluation completed in 3.8 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.61 sec - Pass 2 of 4: Completed in 0.79 sec - Pass 3 of 4: Completed in 0.56 sec - Pass 4 of 4: Completed in 1.2 sec Evaluation completed in 3.7 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.62 sec - Pass 2 of 4: Completed in 0.85 sec - Pass 3 of 4: Completed in 0.56 sec - Pass 4 of 4: Completed in 1 sec Evaluation completed in 3.6 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.61 sec - Pass 2 of 4: Completed in 0.86 sec - Pass 3 of 4: Completed in 1.1 sec - Pass 4 of 4: Completed in 0.96 sec Evaluation completed in 4.1 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.65 sec - Pass 2 of 4: Completed in 0.8 sec - Pass 3 of 4: Completed in 0.59 sec - Pass 4 of 4: Completed in 0.86 sec Evaluation completed in 3.5 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.69 sec - Pass 2 of 4: Completed in 0.84 sec - Pass 3 of 4: Completed in 0.53 sec - Pass 4 of 4: Completed in 0.83 sec Evaluation completed in 3.5 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.76 sec Evaluation completed in 0.89 sec | 12 | Accept | 0.1008 | 90.267 | 0.1008 | 0.10086 | 179 | Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.32 sec Evaluation completed in 0.45 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.9 sec Evaluation completed in 1.1 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.58 sec - Pass 2 of 4: Completed in 0.71 sec - Pass 3 of 4: Completed in 0.53 sec - Pass 4 of 4: Completed in 0.77 sec Evaluation completed in 3.2 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.49 sec - Pass 2 of 4: Completed in 0.69 sec - Pass 3 of 4: Completed in 0.58 sec - Pass 4 of 4: Completed in 0.77 sec Evaluation completed in 3.1 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.52 sec - Pass 2 of 4: Completed in 0.71 sec - Pass 3 of 4: Completed in 0.51 sec - Pass 4 of 4: Completed in 0.78 sec Evaluation completed in 3.1 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.54 sec - Pass 2 of 4: Completed in 0.7 sec - Pass 3 of 4: Completed in 0.54 sec - Pass 4 of 4: Completed in 0.72 sec Evaluation completed in 3.1 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.54 sec - Pass 2 of 4: Completed in 0.74 sec - Pass 3 of 4: Completed in 0.51 sec - Pass 4 of 4: Completed in 1.3 sec Evaluation completed in 3.6 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.54 sec - Pass 2 of 4: Completed in 0.78 sec - Pass 3 of 4: Completed in 0.59 sec - Pass 4 of 4: Completed in 0.74 sec Evaluation completed in 3.2 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.83 sec Evaluation completed in 0.97 sec | 13 | Accept | 0.11126 | 32.134 | 0.1008 | 0.10084 | 10251 | Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.32 sec Evaluation completed in 0.45 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.85 sec Evaluation completed in 0.99 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.51 sec - Pass 2 of 4: Completed in 0.75 sec - Pass 3 of 4: Completed in 0.55 sec - Pass 4 of 4: Completed in 0.74 sec Evaluation completed in 3.1 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.5 sec - Pass 2 of 4: Completed in 0.7 sec - Pass 3 of 4: Completed in 0.57 sec - Pass 4 of 4: Completed in 0.78 sec Evaluation completed in 3.1 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.5 sec - Pass 2 of 4: Completed in 0.68 sec - Pass 3 of 4: Completed in 0.53 sec - Pass 4 of 4: Completed in 0.79 sec Evaluation completed in 3 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.5 sec - Pass 2 of 4: Completed in 1.3 sec - Pass 3 of 4: Completed in 0.54 sec - Pass 4 of 4: Completed in 0.91 sec Evaluation completed in 3.7 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.53 sec - Pass 2 of 4: Completed in 1.2 sec - Pass 3 of 4: Completed in 0.59 sec - Pass 4 of 4: Completed in 0.86 sec Evaluation completed in 3.7 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.51 sec - Pass 2 of 4: Completed in 0.71 sec - Pass 3 of 4: Completed in 0.59 sec - Pass 4 of 4: Completed in 1 sec Evaluation completed in 3.4 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.56 sec - Pass 2 of 4: Completed in 0.71 sec - Pass 3 of 4: Completed in 0.64 sec - Pass 4 of 4: Completed in 0.99 sec Evaluation completed in 3.4 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.54 sec - Pass 2 of 4: Completed in 1.2 sec - Pass 3 of 4: Completed in 0.58 sec - Pass 4 of 4: Completed in 0.94 sec Evaluation completed in 3.8 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.51 sec - Pass 2 of 4: Completed in 0.77 sec - Pass 3 of 4: Completed in 0.59 sec - Pass 4 of 4: Completed in 0.9 sec Evaluation completed in 3.3 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.56 sec - Pass 2 of 4: Completed in 0.78 sec - Pass 3 of 4: Completed in 0.56 sec - Pass 4 of 4: Completed in 0.9 sec Evaluation completed in 3.3 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.55 sec - Pass 2 of 4: Completed in 0.72 sec - Pass 3 of 4: Completed in 0.52 sec - Pass 4 of 4: Completed in 0.89 sec Evaluation completed in 3.2 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.58 sec - Pass 2 of 4: Completed in 0.76 sec - Pass 3 of 4: Completed in 0.54 sec - Pass 4 of 4: Completed in 0.8 sec Evaluation completed in 3.3 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.56 sec - Pass 2 of 4: Completed in 1.3 sec - Pass 3 of 4: Completed in 0.61 sec - Pass 4 of 4: Completed in 0.76 sec Evaluation completed in 3.8 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.83 sec Evaluation completed in 0.97 sec | 14 | Accept | 0.10154 | 66.262 | 0.1008 | 0.10085 | 736 | Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.36 sec Evaluation completed in 0.5 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 0.89 sec Evaluation completed in 1 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.53 sec - Pass 2 of 4: Completed in 0.69 sec - Pass 3 of 4: Completed in 0.56 sec - Pass 4 of 4: Completed in 0.74 sec Evaluation completed in 3.1 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.5 sec - Pass 2 of 4: Completed in 0.67 sec - Pass 3 of 4: Completed in 0.56 sec - Pass 4 of 4: Completed in 0.78 sec Evaluation completed in 3.1 sec Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 0.52 sec - Pass 2 of 4: Completed in 0.69 sec - Pass 3 of 4: Completed in 0.54 sec - Pass 4 of 4: Completed in 0.84 sec Evaluation completed in 3.1 sec Evaluating tall expression using the Parallel Pool 'local': Evaluation 0% ...
Mdl =
CompactClassificationTree
ResponseName: 'Y'
CategoricalPredictors: []
ClassNames: [0 1]
ScoreTransform: 'none'
Properties, Methods
FitInfo = struct with no fields.
HyperparameterOptimizationResults =
BayesianOptimization with properties:
ObjectiveFcn: @createObjFcn/tallObjFcn
VariableDescriptions: [4×1 optimizableVariable]
Options: [1×1 struct]
MinObjective: 0.1004
XAtMinObjective: [1×1 table]
MinEstimatedObjective: 0.1008
XAtMinEstimatedObjective: [1×1 table]
NumObjectiveEvaluations: 30
TotalElapsedTime: 3.0367e+03
NextPoint: [1×1 table]
XTrace: [30×1 table]
ObjectiveTrace: [30×1 double]
ConstraintsTrace: []
UserDataTrace: {30×1 cell}
ObjectiveEvaluationTimeTrace: [30×1 double]
IterationTimeTrace: [30×1 double]
ErrorTrace: [30×1 double]
FeasibilityTrace: [30×1 logical]
FeasibilityProbabilityTrace: [30×1 double]
IndexOfMinimumTrace: [30×1 double]
ObjectiveMinimumTrace: [30×1 double]
EstimatedObjectiveMinimumTrace: [30×1 double]
Input Arguments
Tbl — Sample data
table
Sample data used to train the model, specified as a table. Each row of Tbl
corresponds to one observation, and each column corresponds to one predictor variable.
Optionally, Tbl can contain one additional column for the response
variable. Multicolumn variables and cell arrays other than cell arrays of character
vectors are not allowed.
If
Tblcontains the response variable, and you want to use all remaining variables inTblas predictors, then specify the response variable by usingResponseVarName.If
Tblcontains the response variable, and you want to use only a subset of the remaining variables inTblas predictors, then specify a formula by usingformula.If
Tbldoes not contain the response variable, then specify a response variable by usingY. The length of the response variable and the number of rows inTblmust be equal.
ResponseVarName — Response variable name
name of variable in Tbl
Response variable name, specified as the name of a variable in
Tbl.
You must specify ResponseVarName as a character vector or string scalar.
For example, if the response variable Y is
stored as Tbl.Y, then specify it as
"Y". Otherwise, the software
treats all columns of Tbl, including
Y, as predictors when training
the model.
The response variable must be a categorical, character, or string array; a logical or numeric
vector; or a cell array of character vectors. If
Y is a character array, then each
element of the response variable must correspond to one row of
the array.
A good practice is to specify the order of the classes by using the
ClassNames name-value
argument.
Data Types: char | string
formula — Explanatory model of response variable and subset of predictor variables
character vector | string scalar
Explanatory model of the response variable and a subset of the predictor variables,
specified as a character vector or string scalar in the form
"Y~x1+x2+x3". In this form, Y represents the
response variable, and x1, x2, and
x3 represent the predictor variables.
To specify a subset of variables in Tbl as predictors for
training the model, use a formula. If you specify a formula, then the software does not
use any variables in Tbl that do not appear in
formula.
The variable names in the formula must be both variable names in Tbl
(Tbl.Properties.VariableNames) and valid MATLAB® identifiers. You can verify the variable names in Tbl by
using the isvarname function. If the variable names
are not valid, then you can convert them by using the matlab.lang.makeValidName function.
Data Types: char | string
Y — Class labels
numeric vector | categorical vector | logical vector | character array | string array | cell array of character vectors
Class labels, specified as a numeric vector, categorical vector, logical vector, character
array, string array, or cell array of character vectors. Each row of
Y represents the classification of the corresponding row of
X.
When fitting the tree, fitctree considers NaN,
'' (empty character vector), "" (empty
string), <missing>, and <undefined>
values in Y to be missing values. fitctree
does not use observations with missing values for Y in the
fit.
For numeric Y, consider fitting a regression
tree using fitrtree instead.
Data Types: single | double | categorical | logical | char | string | cell
X — Predictor data
numeric matrix
Predictor data, specified as a numeric matrix. Each row of X corresponds
to one observation, and each column corresponds to one predictor variable.
fitctree considers NaN values
in X as missing values. fitctree does
not use observations with all missing values for X in
the fit. fitctree uses observations with some
missing values for X to find splits on variables
for which these observations have valid values.
Data Types: single | double
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: 'CrossVal','on','MinLeafSize',40 specifies a
cross-validated classification tree with a minimum of 40 observations per
leaf.
Note
You cannot use any cross-validation name-value argument together with the
'OptimizeHyperparameters' name-value argument. You can modify the
cross-validation for 'OptimizeHyperparameters' only by using the
'HyperparameterOptimizationOptions' name-value argument.
AlgorithmForCategorical — Algorithm for best categorical predictor split
'Exact' | 'PullLeft' | 'PCA' | 'OVAbyClass'
Algorithm to find the best split on a categorical predictor with
C categories for data and K ≥
3 classes, specified as the comma-separated pair consisting of
'AlgorithmForCategorical' and one of the
following values.
| Value | Description |
|---|---|
'Exact' | Consider all 2C–1 – 1 combinations. |
'PullLeft' | Start with all C categories on the right branch. Consider moving each category to the left branch as it achieves the minimum impurity for the K classes among the remaining categories. From this sequence, choose the split that has the lowest impurity. |
'PCA' | Compute a score for each category using the inner product between the first principal component of a weighted covariance matrix (of the centered class probability matrix) and the vector of class probabilities for that category. Sort the scores in ascending order, and consider all C – 1 splits. |
'OVAbyClass' | Start with all C categories on the right branch. For each class, order the categories based on their probability for that class. For the first class, consider moving each category to the left branch in order, recording the impurity criterion at each move. Repeat for the remaining classes. From this sequence, choose the split that has the minimum impurity. |
fitctree automatically
selects the optimal subset of algorithms for each split using the known
number of classes and levels of a categorical predictor. For
K = 2 classes, fitctree always performs
the exact search. To specify a particular algorithm, use the
'AlgorithmForCategorical' name-value pair
argument.
For more details, see Splitting Categorical Predictors in Classification Trees.
Example: 'AlgorithmForCategorical','PCA'
CategoricalPredictors — Categorical predictors list
vector of positive integers | logical vector | character matrix | string array | cell array of character vectors | 'all'
Categorical predictors list, specified as one of the values in this table.
| Value | Description |
|---|---|
| Vector of positive integers |
Each entry in the vector is an index value indicating that the corresponding predictor is
categorical. The index values are between 1 and If |
| Logical vector |
A |
| Character matrix | Each row of the matrix is the name of a predictor variable. The names must match the entries in PredictorNames. Pad the names with extra blanks so each row of the character matrix has the same length. |
| String array or cell array of character vectors | Each element in the array is the name of a predictor variable. The names must match the entries in PredictorNames. |
"all" | All predictors are categorical. |
By default, if the predictor data is a table
(Tbl), fitctree assumes that a variable is
categorical if it is a logical vector, unordered categorical vector, character array, string
array, or cell array of character vectors. If the predictor data is a matrix
(X), fitctree assumes that all predictors are
continuous. To identify any other predictors as categorical predictors, specify them by using
the CategoricalPredictors name-value argument.
Example: 'CategoricalPredictors','all'
Data Types: single | double | logical | char | string | cell
ClassNames — Names of classes to use for training
categorical array | character array | string array | logical vector | numeric vector | cell array of character vectors
Names of classes to use for training, specified as a categorical, character, or string
array; a logical or numeric vector; or a cell array of character vectors.
ClassNames must have the same data type as the response variable
in Tbl or Y.
If ClassNames is a character array, then each element must correspond to one row of the array.
Use ClassNames to:
Specify the order of the classes during training.
Specify the order of any input or output argument dimension that corresponds to the class order. For example, use
ClassNamesto specify the order of the dimensions ofCostor the column order of classification scores returned bypredict.Select a subset of classes for training. For example, suppose that the set of all distinct class names in
Yis["a","b","c"]. To train the model using observations from classes"a"and"c"only, specify"ClassNames",["a","c"].
The default value for ClassNames is the set of all distinct class names in the response variable in Tbl or Y.
Example: "ClassNames",["b","g"]
Data Types: categorical | char | string | logical | single | double | cell
Cost — Cost of misclassification
square matrix | structure
Cost of misclassification of a point, specified as the comma-separated
pair consisting of 'Cost' and one of the
following:
Square matrix, where
Cost(i,j)is the cost of classifying a point into classjif its true class isi(i.e., the rows correspond to the true class and the columns correspond to the predicted class). To specify the class order for the corresponding rows and columns ofCost, also specify theClassNamesname-value pair argument.Structure
Shaving two fields:S.ClassNamescontaining the group names as a variable of the same data type asY, andS.ClassificationCostscontaining the cost matrix.
The default is Cost(i,j)=1 if
i~=j, and Cost(i,j)=0 if
i=j.
Data Types: single | double | struct
MaxDepth — Maximum tree depth
positive integer
Maximum tree depth, specified as the comma-separated pair consisting
of 'MaxDepth' and a positive integer. Specify a value
for this argument to return a tree that has fewer levels and requires
fewer passes through the tall array to compute. Generally, the algorithm
of fitctree takes one pass through the data and an
additional pass for each tree level. The function does not set a maximum
tree depth, by default.
Note
This option applies only when you use
fitctree on tall arrays. See Tall Arrays for more information.
MaxNumCategories — Maximum category levels
10 (default) | nonnegative scalar value
Maximum category levels, specified as the comma-separated pair
consisting of 'MaxNumCategories' and a nonnegative
scalar value. fitctree splits a
categorical predictor using the exact search algorithm if the predictor
has at most MaxNumCategories levels in the split
node. Otherwise, fitctree finds the best
categorical split using one of the inexact algorithms.
Passing a small value can lead to loss of accuracy and passing a large value can increase computation time and memory overload.
Example: 'MaxNumCategories',8
MaxNumSplits — Maximal number of decision splits
size(X,1) - 1 (default) | nonnegative scalar
Maximal number of decision splits (or branch nodes), specified as the
comma-separated pair consisting of 'MaxNumSplits' and
a nonnegative scalar. fitctree splits
MaxNumSplits or fewer branch nodes. For more
details on splitting behavior, see Algorithms.
Example: 'MaxNumSplits',5
Data Types: single | double
MergeLeaves — Leaf merge flag
'on' (default) | 'off'
Leaf merge flag, specified as the comma-separated pair consisting of
'MergeLeaves' and 'on' or
'off'.
If MergeLeaves is 'on', then
fitctree:
Merges leaves that originate from the same parent node, and that yields a sum of risk values greater than or equal to the risk associated with the parent node
Estimates the optimal sequence of pruned subtrees, but does not prune the classification tree
Otherwise, fitctree does not merge
leaves.
Example: 'MergeLeaves','off'
MinLeafSize — Minimum number of leaf node observations
1 (default) | positive integer value
Minimum number of leaf node observations, specified as the
comma-separated pair consisting of 'MinLeafSize' and
a positive integer value. Each leaf has at least
MinLeafSize observations per tree leaf. If you
supply both MinParentSize and
MinLeafSize, fitctree uses
the setting that gives larger leaves: MinParentSize =
max(MinParentSize,2*MinLeafSize).
Example: 'MinLeafSize',3
Data Types: single | double
MinParentSize — Minimum number of branch node observations
10 (default) | positive integer value
Minimum number of branch node observations, specified as the
comma-separated pair consisting of 'MinParentSize'
and a positive integer value. Each branch node in the tree has at least
MinParentSize observations. If you supply both
MinParentSize and MinLeafSize,
fitctree uses the setting
that gives larger leaves: MinParentSize =
max(MinParentSize,2*MinLeafSize).
Example: 'MinParentSize',8
Data Types: single | double
NumBins — Number of bins for numeric predictors
[](empty) (default) | positive integer scalar
Number of bins for numeric predictors, specified as the comma-separated pair
consisting of 'NumBins' and a positive integer scalar.
If the
'NumBins'value is empty (default), thenfitctreedoes not bin any predictors.If you specify the
'NumBins'value as a positive integer scalar (numBins), thenfitctreebins every numeric predictor into at mostnumBinsequiprobable bins, and then grows trees on the bin indices instead of the original data.The number of bins can be less than
numBinsif a predictor has fewer thannumBinsunique values.fitctreedoes not bin categorical predictors.
When you use a large training data set, this binning option speeds up training but might cause
a potential decrease in accuracy. You can try 'NumBins',50 first, and
then change the value depending on the accuracy and training speed.
A trained model stores the bin edges in the BinEdges property.
Example: 'NumBins',50
Data Types: single | double
NumVariablesToSample — Number of predictors to select at random for each split
'all' (default) | positive integer value
Number of predictors to select at random for each split, specified as the comma-separated pair consisting of 'NumVariablesToSample' and a positive integer value. Alternatively, you can specify 'all' to use all available predictors.
If the training data includes many predictors and you want to analyze predictor
importance, then specify 'NumVariablesToSample' as
'all'. Otherwise, the software might not select some predictors,
underestimating their importance.
To reproduce the random selections, you must set the seed of the random number generator by using rng and specify 'Reproducible',true.
Example: 'NumVariablesToSample',3
Data Types: char | string | single | double
PredictorNames — Predictor variable names
string array of unique names | cell array of unique character vectors
Predictor variable names, specified as a string array of unique names or cell array of unique
character vectors. The functionality of PredictorNames depends on the
way you supply the training data.
If you supply
XandY, then you can usePredictorNamesto assign names to the predictor variables inX.The order of the names in
PredictorNamesmust correspond to the column order ofX. That is,PredictorNames{1}is the name ofX(:,1),PredictorNames{2}is the name ofX(:,2), and so on. Also,size(X,2)andnumel(PredictorNames)must be equal.By default,
PredictorNamesis{'x1','x2',...}.
If you supply
Tbl, then you can usePredictorNamesto choose which predictor variables to use in training. That is,fitctreeuses only the predictor variables inPredictorNamesand the response variable during training.PredictorNamesmust be a subset ofTbl.Properties.VariableNamesand cannot include the name of the response variable.By default,
PredictorNamescontains the names of all predictor variables.A good practice is to specify the predictors for training using either
PredictorNamesorformula, but not both.
Example: "PredictorNames",["SepalLength","SepalWidth","PetalLength","PetalWidth"]
Data Types: string | cell
PredictorSelection — Algorithm used to select the best split predictor
'allsplits' (default) | 'curvature' | 'interaction-curvature'
Algorithm used to select the best split predictor at each node,
specified as the comma-separated pair consisting of
'PredictorSelection' and a value in this
table.
| Value | Description |
|---|---|
'allsplits' | Standard CART — Selects the split predictor that maximizes the split-criterion gain over all possible splits of all predictors [1]. |
'curvature' | Curvature test — Selects the split predictor that minimizes the p-value of chi-square tests of independence between each predictor and the response [4]. Training speed is similar to standard CART. |
'interaction-curvature' | Interaction test — Chooses the split predictor that minimizes the p-value of chi-square tests of independence between each predictor and the response, and that minimizes the p-value of a chi-square test of independence between each pair of predictors and response [3]. Training speed can be slower than standard CART. |
For 'curvature' and
'interaction-curvature', if all tests yield
p-values greater than 0.05, then
fitctree stops splitting nodes.
Tip
Standard CART tends to select split predictors containing many distinct values, e.g., continuous variables, over those containing few distinct values, e.g., categorical variables [4]. Consider specifying the curvature or interaction test if any of the following are true:
If there are predictors that have relatively fewer distinct values than other predictors, for example, if the predictor data set is heterogeneous.
If an analysis of predictor importance is your goal. For more on predictor importance estimation, see
predictorImportanceand Introduction to Feature Selection.
Trees grown using standard CART are not sensitive to predictor variable interactions. Also, such trees are less likely to identify important variables in the presence of many irrelevant predictors than the application of the interaction test. Therefore, to account for predictor interactions and identify importance variables in the presence of many irrelevant variables, specify the interaction test [3].
Prediction speed is unaffected by the value of
'PredictorSelection'.
For details on how fitctree selects split
predictors, see Node Splitting Rules and Choose Split Predictor Selection Technique.
Example: 'PredictorSelection','curvature'
Prior — Prior probabilities
'empirical' (default) | 'uniform' | vector of scalar values | structure
Prior probabilities for each class, specified as one of the following:
Character vector or string scalar.
Vector (one scalar value for each class). To specify the class order for the corresponding elements of
'Prior', set the'ClassNames'name-value argument.Structure
Swith two fields.S.ClassNamescontains the class names as a variable of the same type as the response variable inYorTbl.S.ClassProbscontains a vector of corresponding probabilities.
fitctree normalizes the weights in each class
('Weights') to add up to the value of the prior probability of
the respective class.
Example: 'Prior','uniform'
Data Types: char | string | single | double | struct
Prune — Flag to estimate optimal sequence of pruned subtrees
'on' (default) | 'off'
Flag to estimate the optimal sequence of pruned subtrees, specified as
the comma-separated pair consisting of 'Prune' and
'on' or 'off'.
If Prune is 'on', then
fitctree grows the classification tree
without pruning it, but estimates the optimal sequence of pruned
subtrees. If Prune is 'off' and
MergeLeaves is also 'off',
then fitctree grows the classification tree
without estimating the optimal sequence of pruned subtrees.
To prune a trained ClassificationTree model,
pass it to prune.
Example: 'Prune','off'
PruneCriterion — Pruning criterion
'error' (default) | 'impurity'
Pruning criterion, specified as the comma-separated pair consisting of
'PruneCriterion' and 'error'
or 'impurity'.
If you specify 'impurity', then
fitctree uses the impurity measure specified
by the 'SplitCriterion' name-value pair
argument.
For details, see Impurity and Node Error.
Example: 'PruneCriterion','impurity'
Reproducible — Flag to enforce reproducibility
false (logical 0) (default) | true (logical 1)
Flag to enforce reproducibility over repeated runs of training a model, specified as the
comma-separated pair consisting of 'Reproducible' and either
false or true.
If 'NumVariablesToSample' is not 'all', then the
software selects predictors at random for each split. To reproduce the random
selections, you must specify 'Reproducible',true and set the seed of
the random number generator by using rng. Note that setting 'Reproducible' to
true can slow down training.
Example: 'Reproducible',true
Data Types: logical
ResponseName — Response variable name
'Y' (default) | character vector | string scalar
Response variable name, specified as the comma-separated pair
consisting of 'ResponseName' and a character vector
or string scalar representing the name of the response variable.
This name-value pair is not valid when using the
ResponseVarName or formula
input arguments.
Example: 'ResponseName','IrisType'
Data Types: char | string
ScoreTransform — Score transformation
"none" (default) | "doublelogit" | "invlogit" | "ismax" | "logit" | function handle | ...
Score transformation, specified as a character vector, string scalar, or function handle.
This table summarizes the available character vectors and string scalars.
| Value | Description |
|---|---|
"doublelogit" | 1/(1 + e–2x) |
"invlogit" | log(x / (1 – x)) |
"ismax" | Sets the score for the class with the largest score to 1, and sets the scores for all other classes to 0 |
"logit" | 1/(1 + e–x) |
"none" or "identity" | x (no transformation) |
"sign" | –1 for x < 0 0 for x = 0 1 for x > 0 |
"symmetric" | 2x – 1 |
"symmetricismax" | Sets the score for the class with the largest score to 1, and sets the scores for all other classes to –1 |
"symmetriclogit" | 2/(1 + e–x) – 1 |
For a MATLAB function or a function you define, use its function handle for the score transform. The function handle must accept a matrix (the original scores) and return a matrix of the same size (the transformed scores).
Example: "ScoreTransform","logit"
Data Types: char | string | function_handle
SplitCriterion — Split criterion
'gdi' (default) | 'twoing' | 'deviance'
Split criterion, specified as the comma-separated pair consisting of
'SplitCriterion' and 'gdi'
(Gini's diversity index), 'twoing' for the twoing
rule, or 'deviance' for maximum deviance reduction
(also known as cross entropy).
For details, see Impurity and Node Error.
Example: 'SplitCriterion','deviance'
Surrogate — Surrogate decision splits flag
'off' (default) | 'on' | 'all' | positive integer value
Surrogate decision
splits flag, specified as the comma-separated pair consisting
of 'Surrogate' and 'on',
'off', 'all', or a positive
integer value.
When set to
'on',fitctreefinds at most 10 surrogate splits at each branch node.When set to
'all',fitctreefinds all surrogate splits at each branch node. The'all'setting can use considerable time and memory.When set to a positive integer value,
fitctreefinds at most the specified number of surrogate splits at each branch node.
Use surrogate splits to improve the accuracy of predictions for data with missing values. The setting also lets you compute measures of predictive association between predictors. For more details, see Node Splitting Rules.
Example: 'Surrogate','on'
Data Types: single | double | char | string
Weights — Observation weights
ones(size(X,1),1) (default) | vector of scalar values | name of variable in Tbl
Observation weights, specified as the comma-separated pair consisting of 'Weights' and a vector of scalar values or the name of a variable in Tbl. The software weights the observations in each row of X or Tbl with the corresponding value in Weights. The size of Weights must equal the number of rows in X or Tbl.
If you specify the input data as a table Tbl, then
Weights can be the name of a variable in Tbl
that contains a numeric vector. In this case, you must specify
Weights as a character vector or string scalar. For example, if
the weights vector W is stored as Tbl.W, then
specify it as 'W'. Otherwise, the software treats all columns of
Tbl, including W, as predictors when training
the model.
fitctree normalizes the weights in each class to add up to the value
of the prior probability of the respective class.
Data Types: single | double | char | string
CrossVal — Flag to grow cross-validated decision tree
'off' (default) | 'on'
Flag to grow a cross-validated decision tree, specified as the
comma-separated pair consisting of 'CrossVal' and
'on' or 'off'.
If 'on', fitctree grows a
cross-validated decision tree with 10 folds. You can override this
cross-validation setting using one of the 'KFold',
'Holdout', 'Leaveout', or
'CVPartition' name-value pair arguments. You can
only use one of these four arguments at a time when creating a
cross-validated tree.
Alternatively, cross-validate tree later using
the crossval method.
Example: 'CrossVal','on'
CVPartition — Partition for cross-validated tree
cvpartition object
Partition to use in a cross-validated tree, specified as the
comma-separated pair consisting of 'CVPartition' and
an object created using cvpartition.
If you use 'CVPartition', you cannot use any of the
'KFold', 'Holdout', or
'Leaveout' name-value pair arguments.
Holdout — Fraction of data for holdout validation
0 (default) | scalar value in the range [0,1]
Fraction of data used for holdout validation, specified as the
comma-separated pair consisting of 'Holdout' and a
scalar value in the range [0,1]. Holdout validation
tests the specified fraction of the data, and uses the rest of the data
for training.
If you use 'Holdout', you cannot use any of the
'CVPartition', 'KFold', or
'Leaveout' name-value pair arguments.
Example: 'Holdout',0.1
Data Types: single | double
KFold — Number of folds
10 (default) | positive integer value greater than 1
Number of folds to use in a cross-validated classifier, specified
as the comma-separated pair consisting of 'KFold' and
a positive integer value greater than 1. If you specify, e.g., 'KFold',k,
then the software:
Randomly partitions the data into k sets
For each set, reserves the set as validation data, and trains the model using the other k – 1 sets
Stores the
kcompact, trained models in the cells of ak-by-1 cell vector in theTrainedproperty of the cross-validated model.
To create a cross-validated model, you can use one of these
four options only: CVPartition, Holdout, KFold,
or Leaveout.
Example: 'KFold',8
Data Types: single | double
Leaveout — Leave-one-out cross-validation flag
'off' (default) | 'on'
Leave-one-out cross-validation flag, specified as the comma-separated
pair consisting of 'Leaveout' and
'on' or 'off'. Specify
'on' to use leave-one-out
cross-validation.
If you use 'Leaveout', you cannot use any of the
'CVPartition', 'Holdout', or
'KFold' name-value pair arguments.
Example: 'Leaveout','on'
OptimizeHyperparameters — Parameters to optimize
'none' (default) | 'auto' | 'all' | string array or cell array of eligible parameter names | vector of optimizableVariable objects
Parameters to optimize, specified as the comma-separated pair
consisting of 'OptimizeHyperparameters' and one of
the following:
'none'— Do not optimize.'auto'— Use{'MinLeafSize'}'all'— Optimize all eligible parameters.String array or cell array of eligible parameter names
Vector of
optimizableVariableobjects, typically the output ofhyperparameters
The optimization attempts to minimize the cross-validation loss
(error) for fitctree by varying the parameters. For
information about cross-validation loss (albeit in a different context),
see Classification Loss. To control the
cross-validation type and other aspects of the optimization, use the
HyperparameterOptimizationOptions name-value
pair.
Note
The values of OptimizeHyperparameters override any values you specify
using other name-value arguments. For example, setting
OptimizeHyperparameters to "auto" causes
fitctree to optimize hyperparameters corresponding to the
"auto" option and to ignore any specified values for the
hyperparameters.
The eligible parameters for fitctree are:
MaxNumSplits—fitctreesearches among integers, by default log-scaled in the range[1,max(2,NumObservations-1)].MinLeafSize—fitctreesearches among integers, by default log-scaled in the range[1,max(2,floor(NumObservations/2))].SplitCriterion— For two classes,fitctreesearches among'gdi'and'deviance'. For three or more classes,fitctreealso searches among'twoing'.NumVariablesToSample—fitctreedoes not optimize over this hyperparameter. If you passNumVariablesToSampleas a parameter name,fitctreesimply uses the full number of predictors. However,fitcensembledoes optimize over this hyperparameter.
Set nondefault parameters by passing a vector of
optimizableVariable objects that have nondefault
values. For example,
load fisheriris params = hyperparameters('fitctree',meas,species); params(1).Range = [1,30];
Pass params as the value of
OptimizeHyperparameters.
By default, the iterative display appears at the command line,
and plots appear according to the number of hyperparameters in the optimization. For the
optimization and plots, the objective function is the misclassification rate. To control the
iterative display, set the Verbose field of the
HyperparameterOptimizationOptions name-value argument. To control the
plots, set the ShowPlots field of the
HyperparameterOptimizationOptions name-value argument.
For an example, see Optimize Classification Tree.
Example: 'auto'
HyperparameterOptimizationOptions — Options for optimization
structure
Options for optimization, specified as a structure. This argument modifies the effect of the
OptimizeHyperparameters name-value argument. All fields in the
structure are optional.
| Field Name | Values | Default |
|---|---|---|
Optimizer |
| 'bayesopt' |
AcquisitionFunctionName |
Acquisition functions whose names include
| 'expected-improvement-per-second-plus' |
MaxObjectiveEvaluations | Maximum number of objective function evaluations. | 30 for 'bayesopt' and
'randomsearch', and the entire grid for
'gridsearch' |
MaxTime | Time limit, specified as a positive real scalar. The time limit is in seconds, as
measured by | Inf |
NumGridDivisions | For 'gridsearch', the number of values in each dimension. The value can be
a vector of positive integers giving the number of
values for each dimension, or a scalar that
applies to all dimensions. This field is ignored
for categorical variables. | 10 |
ShowPlots | Logical value indicating whether to show plots. If true, this field plots
the best observed objective function value against the iteration number. If you
use Bayesian optimization (Optimizer is
'bayesopt'), then this field also plots the best
estimated objective function value. The best observed objective function values
and best estimated objective function values correspond to the values in the
BestSoFar (observed) and BestSoFar
(estim.) columns of the iterative display, respectively. You can
find these values in the properties ObjectiveMinimumTrace and EstimatedObjectiveMinimumTrace of
Mdl.HyperparameterOptimizationResults. If the problem
includes one or two optimization parameters for Bayesian optimization, then
ShowPlots also plots a model of the objective function
against the parameters. | true |
SaveIntermediateResults | Logical value indicating whether to save results when Optimizer is
'bayesopt'. If
true, this field overwrites a
workspace variable named
'BayesoptResults' at each
iteration. The variable is a BayesianOptimization object. | false |
Verbose | Display at the command line:
For details, see the | 1 |
UseParallel | Logical value indicating whether to run Bayesian optimization in parallel, which requires Parallel Computing Toolbox™. Due to the nonreproducibility of parallel timing, parallel Bayesian optimization does not necessarily yield reproducible results. For details, see Parallel Bayesian Optimization. | false |
Repartition | Logical value indicating whether to repartition the cross-validation at every
iteration. If this field is The setting
| false |
| Use no more than one of the following three options. | ||
CVPartition | A cvpartition object, as created by cvpartition | 'Kfold',5 if you do not specify a cross-validation
field |
Holdout | A scalar in the range (0,1) representing the holdout fraction | |
Kfold | An integer greater than 1 | |
Example: 'HyperparameterOptimizationOptions',struct('MaxObjectiveEvaluations',60)
Data Types: struct
Output Arguments
tree — Classification tree
classification tree object
Classification tree, returned as a classification tree object.
Using the 'CrossVal', 'KFold',
'Holdout', 'Leaveout', or
'CVPartition' options results in a tree of class
ClassificationPartitionedModel.
You cannot use a partitioned tree for prediction, so this kind of tree does
not have a predict method. Instead, use
kfoldPredict to predict
responses for observations not used for training.
Otherwise, tree is of class ClassificationTree, and you can
use the predict method to make
predictions.
More About
Curvature Test
The curvature test is a statistical test assessing the null hypothesis that two variables are unassociated.
The curvature test between predictor variable x and y is conducted using this process.
If x is continuous, then partition it into its quartiles. Create a nominal variable that bins observations according to which section of the partition they occupy. If there are missing values, then create an extra bin for them.
For each level in the partitioned predictor j = 1...J and class in the response k = 1,...,K, compute the weighted proportion of observations in class k
wi is the weight of observation i, , I is the indicator function, and n is the sample size. If all observations have the same weight, then , where njk is the number of observations in level j of the predictor that are in class k.
Compute the test statistic
, that is, the marginal probability of observing the predictor at level j. , that is the marginal probability of observing class k. If n is large enough, then t is distributed as a χ2 with (K – 1)(J – 1) degrees of freedom.
If the p-value for the test is less than 0.05, then reject the null hypothesis that there is no association between x and y.
When determining the best split predictor at each node, the standard CART algorithm prefers to select continuous predictors that have many levels. Sometimes, such a selection can be spurious and can also mask more important predictors that have fewer levels, such as categorical predictors.
The curvature test can be applied instead of standard CART to determine the best split predictor at each node. In that case, the best split predictor variable is the one that minimizes the significant p-values (those less than 0.05) of curvature tests between each predictor and the response variable. Such a selection is robust to the number of levels in individual predictors.
Note
If levels of a predictor are pure for a particular class, then
fitctree merges those levels. Therefore, in step 3
of the algorithm, J can be less than the actual number of
levels in the predictor. For example, if x has 4 levels, and
all observations in bins 1 and 2 belong to class 1, then those levels are pure
for class 1. Consequently, fitctree merges the
observations in bins 1 and 2, and J reduces to 3.
For more details on how the curvature test applies to growing classification trees, see Node Splitting Rules and [4].
Impurity and Node Error
A decision tree splits nodes based on either impurity or node error.
Impurity means one of several things, depending on your choice of the
SplitCriterion name-value
argument:
Gini's Diversity Index (
gdi) — The Gini index of a node iswhere the sum is over the classes i at the node, and p(i) is the observed fraction of classes with class i that reach the node. A node with just one class (a pure node) has Gini index
0; otherwise, the Gini index is positive. So the Gini index is a measure of node impurity.Deviance (
"deviance") — With p(i) defined the same as for the Gini index, the deviance of a node isA pure node has deviance
0; otherwise, the deviance is positive.Twoing rule (
"twoing") — Twoing is not a purity measure of a node, but is a different measure for deciding how to split a node. Let L(i) denote the fraction of members of class i in the left child node after a split, and R(i) denote the fraction of members of class i in the right child node after a split. Choose the split criterion to maximizewhere P(L) and P(R) are the fractions of observations that split to the left and right, respectively. If the expression is large, the split made each child node purer. Similarly, if the expression is small, the split made each child node similar to each other and, therefore, similar to the parent node. The split did not increase node purity.
Node error — The node error is the fraction of misclassified classes at a node. If j is the class with the largest number of training samples at a node, the node error is
1 – p(j).
Interaction Test
The interaction test is a statistical test that assesses the null hypothesis that there is no interaction between a pair of predictor variables and the response variable.
The interaction test assessing the association between predictor variables x1 and x2 with respect to y is conducted using this process.
If x1 or x2 is continuous, then partition that variable into its quartiles. Create a nominal variable that bins observations according to which section of the partition they occupy. If there are missing values, then create an extra bin for them.
Create the nominal variable z with J = J1J2 levels that assigns an index to observation i according to which levels of x1 and x2 it belongs. Remove any levels of z that do not correspond to any observations.
Conduct a curvature test between z and y.
When growing decision trees, if there are important interactions between pairs of predictors, but there are also many other less important predictors in the data, then standard CART tends to miss the important interactions. However, conducting curvature and interaction tests for predictor selection instead can improve detection of important interactions, which can yield more accurate decision trees.
For more details on how the interaction test applies to growing decision trees, see Curvature Test, Node Splitting Rules and [3].
Predictive Measure of Association
The predictive measure of association is a value that indicates the similarity between decision rules that split observations. Among all possible decision splits that are compared to the optimal split (found by growing the tree), the best surrogate decision split yields the maximum predictive measure of association. The second-best surrogate split has the second-largest predictive measure of association.
Suppose xj and xk are predictor variables j and k, respectively, and j ≠ k. At node t, the predictive measure of association between the optimal split xj < u and a surrogate split xk < v is
PL is the proportion of observations in node t, such that xj < u. The subscript L stands for the left child of node t.
PR is the proportion of observations in node t, such that xj ≥ u. The subscript R stands for the right child of node t.
is the proportion of observations at node t, such that xj < u and xk < v.
is the proportion of observations at node t, such that xj ≥ u and xk ≥ v.
Observations with missing values for xj or xk do not contribute to the proportion calculations.
λjk is a value in (–∞,1]. If λjk > 0, then xk < v is a worthwhile surrogate split for xj < u.
Surrogate Decision Splits
A surrogate decision split is an alternative to the optimal decision split at a given node in a decision tree. The optimal split is found by growing the tree; the surrogate split uses a similar or correlated predictor variable and split criterion.
When the value of the optimal split predictor for an observation is missing, the observation is sent to the left or right child node using the best surrogate predictor. When the value of the best surrogate split predictor for the observation is also missing, the observation is sent to the left or right child node using the second-best surrogate predictor, and so on. Candidate splits are sorted in descending order by their predictive measure of association.
Tips
By default,
Pruneis'on'. However, this specification does not prune the classification tree. To prune a trained classification tree, pass the classification tree toprune.After training a model, you can generate C/C++ code that predicts labels for new data. Generating C/C++ code requires MATLAB Coder™. For details, see Introduction to Code Generation.
Algorithms
Node Splitting Rules
fitctree uses these processes to determine how to split
node t.
For standard CART (that is, if
PredictorSelectionis'allpairs') and for all predictors xi, i = 1,...,p:fitctreecomputes the weighted impurity of node t, it. For supported impurity measures, seeSplitCriterion.fitctreeestimates the probability that an observation is in node t usingwj is the weight of observation j, and T is the set of all observation indices in node t. If you do not specify
PriororWeights, then wj = 1/n, where n is the sample size.fitctreesorts xi in ascending order. Each element of the sorted predictor is a splitting candidate or cut point.fitctreestores any indices corresponding to missing values in the set TU, which is the unsplit set.fitctreedetermines the best way to split node t using xi by maximizing the impurity gain (ΔI) over all splitting candidates. That is, for all splitting candidates in xi:fitctreesplits the observations in node t into left and right child nodes (tL and tR, respectively).fitctreecomputes ΔI. Suppose that for a particular splitting candidate, tL and tR contain observation indices in the sets TL and TR, respectively.If xi does not contain any missing values, then the impurity gain for the current splitting candidate is
If xi contains missing values then, assuming that the observations are missing at random, the impurity gain is
T – TU is the set of all observation indices in node t that are not missing.
If you use surrogate decision splits, then:
fitctreecomputes the predictive measures of association between the decision split xj < u and all possible decision splits xk < v, j ≠ k.fitctreesorts the possible alternative decision splits in descending order by their predictive measure of association with the optimal split. The surrogate split is the decision split yielding the largest measure.fitctreedecides the child node assignments for observations with a missing value for xi using the surrogate split. If the surrogate predictor also contains a missing value, thenfitctreeuses the decision split with the second largest measure, and so on, until there are no other surrogates. It is possible forfitctreeto split two different observations at node t using two different surrogate splits. For example, suppose the predictors x1 and x2 are the best and second best surrogates, respectively, for the predictor xi, i ∉ {1,2}, at node t. If observation m of predictor xi is missing (i.e., xmi is missing), but xm1 is not missing, then x1 is the surrogate predictor for observation xmi. If observations x(m + 1),i and x(m + 1),1 are missing, but x(m + 1),2 is not missing, then x2 is the surrogate predictor for observation m + 1.fitctreeuses the appropriate impurity gain formula. That is, iffitctreefails to assign all missing observations in node t to children nodes using surrogate splits, then the impurity gain is ΔIU. Otherwise,fitctreeuses ΔI for the impurity gain.
fitctreechooses the candidate that yields the largest impurity gain.
fitctreesplits the predictor variable at the cut point that maximizes the impurity gain.For the curvature test (that is, if
PredictorSelectionis'curvature'):fitctreeconducts curvature tests between each predictor and the response for observations in node t.If all p-values are at least 0.05, then
fitctreedoes not split node t.If there is a minimal p-value, then
fitctreechooses the corresponding predictor to split node t.If more than one p-value is zero due to underflow, then
fitctreeapplies standard CART to the corresponding predictors to choose the split predictor.
If
fitctreechooses a split predictor, then it uses standard CART to choose the cut point (see step 4 in the standard CART process).
For the interaction test (that is, if
PredictorSelectionis'interaction-curvature'):For observations in node t,
fitctreeconducts curvature tests between each predictor and the response and interaction tests between each pair of predictors and the response.If all p-values are at least 0.05, then
fitctreedoes not split node t.If there is a minimal p-value and it is the result of a curvature test, then
fitctreechooses the corresponding predictor to split node t.If there is a minimal p-value and it is the result of an interaction test, then
fitctreechooses the split predictor using standard CART on the corresponding pair of predictors.If more than one p-value is zero due to underflow, then
fitctreeapplies standard CART to the corresponding predictors to choose the split predictor.
If
fitctreechooses a split predictor, then it uses standard CART to choose the cut point (see step 4 in the standard CART process).
Tree Depth Control
If
MergeLeavesis'on'andPruneCriterionis'error'(which are the default values for these name-value pair arguments), then the software applies pruning only to the leaves and by using classification error. This specification amounts to merging leaves that share the most popular class per leaf.To accommodate
MaxNumSplits,fitctreesplits all nodes in the current layer, and then counts the number of branch nodes. A layer is the set of nodes that are equidistant from the root node. If the number of branch nodes exceedsMaxNumSplits,fitctreefollows this procedure:Determine how many branch nodes in the current layer must be unsplit so that there are at most
MaxNumSplitsbranch nodes.Sort the branch nodes by their impurity gains.
Unsplit the number of least successful branches.
Return the decision tree grown so far.
This procedure produces maximally balanced trees.
The software splits branch nodes layer by layer until at least one of these events occurs:
There are
MaxNumSplitsbranch nodes.A proposed split causes the number of observations in at least one branch node to be fewer than
MinParentSize.A proposed split causes the number of observations in at least one leaf node to be fewer than
MinLeafSize.The algorithm cannot find a good split within a layer (i.e., the pruning criterion (see
PruneCriterion), does not improve for all proposed splits in a layer). A special case is when all nodes are pure (i.e., all observations in the node have the same class).For values
'curvature'or'interaction-curvature'ofPredictorSelection, all tests yield p-values greater than 0.05.
MaxNumSplitsandMinLeafSizedo not affect splitting at their default values. Therefore, if you set'MaxNumSplits', splitting might stop due to the value ofMinParentSize, beforeMaxNumSplitssplits occur.
Parallelization
For dual-core systems and above, fitctree parallelizes
training decision trees using Intel® Threading Building Blocks (TBB). For details on Intel TBB, see https://www.intel.com/content/www/us/en/developer/tools/oneapi/onetbb.html.
Cost, Prior, and Weights
If you specify the Cost,
Prior, and Weights name-value arguments, the
output model object stores the specified values in the Cost,
Prior, and W properties, respectively. The
Cost property stores the user-specified cost matrix as is. The
Prior and W properties store the prior probabilities
and observation weights, respectively, after normalization. For details, see Misclassification Cost Matrix, Prior Probabilities, and Observation Weights.
References
[1] Breiman, L., J. Friedman, R. Olshen, and C. Stone. Classification and Regression Trees. Boca Raton, FL: CRC Press, 1984.
[2] Coppersmith, D., S. J. Hong, and J. R. M. Hosking. “Partitioning Nominal Attributes in Decision Trees.” Data Mining and Knowledge Discovery, Vol. 3, 1999, pp. 197–217.
[3] Loh, W.Y. “Regression Trees with Unbiased Variable Selection and Interaction Detection.” Statistica Sinica, Vol. 12, 2002, pp. 361–386.
[4] Loh, W.Y. and Y.S. Shih. “Split Selection Methods for Classification Trees.” Statistica Sinica, Vol. 7, 1997, pp. 815–840.
Extended Capabilities
Tall Arrays
Calculate with arrays that have more rows than fit in memory.
Usage notes and limitations:
Supported syntaxes are:
tree = fitctree(Tbl,Y)tree = fitctree(X,Y)tree = fitctree(___,Name,Value)[tree,FitInfo,HyperparameterOptimizationResults] = fitctree(___,Name,Value)—fitctreereturns the additional output argumentsFitInfoandHyperparameterOptimizationResultswhen you specify the'OptimizeHyperparameters'name-value pair argument.
The
FitInfooutput argument is an empty structure array currently reserved for possible future use.The
HyperparameterOptimizationResultsoutput argument is aBayesianOptimizationobject or a table of hyperparameters with associated values that describe the cross-validation optimization of hyperparameters.'HyperparameterOptimizationResults'is nonempty when the'OptimizeHyperparameters'name-value pair argument is nonempty at the time you create the model. The values in'HyperparameterOptimizationResults'depend on the value you specify for the'HyperparameterOptimizationOptions'name-value pair argument when you create the model.If you specify
'bayesopt'(default), thenHyperparameterOptimizationResultsis an object of classBayesianOptimization.If you specify
'gridsearch'or'randomsearch', thenHyperparameterOptimizationResultsis a table of the hyperparameters used, observed objective function values (cross-validation loss), and rank of observations from lowest (best) to highest (worst).
Supported name-value pair arguments, and any differences, are:
'AlgorithmForCategorical''CategoricalPredictors''ClassNames''Cost''HyperparameterOptimizationOptions'— For cross-validation, tall optimization supports only'Holdout'validation. By default, the software selects and reserves 20% of the data as holdout validation data, and trains the model using the rest of the data. You can specify a different value for the holdout fraction by using this argument. For example, specify'HyperparameterOptimizationOptions',struct('Holdout',0.3)to reserve 30% of the data as validation data.'MaxNumCategories''MaxNumSplits'— for tall optimization,fitctreesearches among integers, by default log-scaled in the range[1,max(2,min(10000,NumObservations-1))].'MergeLeaves''MinLeafSize''MinParentSize''NumVariablesToSample''OptimizeHyperparameters''PredictorNames''Prior''ResponseName''ScoreTransform''SplitCriterion''Weights'
This additional name-value pair argument is specific to tall arrays:
'MaxDepth'— A positive integer specifying the maximum depth of the output tree. Specify a value for this argument to return a tree that has fewer levels and requires fewer passes through the tall array to compute. Generally, the algorithm offitctreetakes one pass through the data and an additional pass for each tree level. The function does not set a maximum tree depth, by default.
For more information, see Tall Arrays.
Automatic Parallel Support
Accelerate code by automatically running computation in parallel using Parallel Computing Toolbox™.
To perform parallel hyperparameter optimization, use the
'HyperparameterOptimizationOptions', struct('UseParallel',true)
name-value argument in the call to the fitctree function.
For more information on parallel hyperparameter optimization, see Parallel Bayesian Optimization.
For general information about parallel computing, see Run MATLAB Functions with Automatic Parallel Support (Parallel Computing Toolbox).
GPU Arrays
Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.
Usage notes and limitations:
fitctreedoes not support surrogate splits. You can specify the name-value argumentSurrogateonly as"off".For data with categorical predictors, the following apply:
For multiclass classification,
fitctreesupports only theOVAbyClassalgorithm for finding the best split.You can specify the name-value argument
NumVariablesToSampleonly as"all".
You can specify the name-value argument
PredictorSelectiononly as"allsplits".fitctreefits the model on a GPU if one of the following applies:The input argument
Xis agpuArrayobjectThe input argument
TblcontainsgpuArraypredictor variables
Note that
fitctreemight not execute faster on a GPU than a CPU for deeper decision trees.
For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Version History
Introduced in R2014a
Commande MATLAB
Vous avez cliqué sur un lien qui correspond à cette commande MATLAB :
Pour exécuter la commande, saisissez-la dans la fenêtre de commande de MATLAB. Les navigateurs web ne supportent pas les commandes MATLAB.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)