基于MATLAB 的传感器融合与跟踪——点目标
作者 : 刘亮、MathWorks
在ADAS/AD系统中,传感器融合是实现各传感器信息互补,提高目标状态精度,满足ISO-26262 ASIL功能安全等级的重要方法,其作用于感知层,作为后续规划与决策层,执行层的输入,重要性不言而喻。
传感器融合一般分为数据级融合,特征级融合,决策级融合。数据级融合一般用于同类型传感器融合;目前常见的1R1V或5R1V系统中采用Vision和Radar的融合, 以及AD系统中采用的LiDAR与Radar融合主要是特征级融合,即对多传感器目标状态信息进行融合;决策级融合一般针对具体功能利用不同传感器的决策与规划结果结合优先级在控制算法层面可以实现。
还记得之前一位做传感器融合的德国工程师给OEM介绍传感器融合直接使用了一词“Magic”。MATLAB and Simulink提供了如GNN,JPDA,TOMHT,PHD,KF/EKF/UKF, PF, IMM等多种跟踪器及滤波器算法。本文以Multiple Target Tracking点目标跟踪为例介绍下Vision和Radar融合“Magic”,后续再单独介绍扩展目标跟踪。
图1所示为多目标跟踪系统框架图,各传感器输出目标探测Detections经数据处理作为输入,Assignment组件根据Gating组件中判断的门限范围内的Detections与Tracks进行目标关联;Track Maintenance组件对Tracks进行新增/更新/删除管理;Filtering组件通过测量值进行更新得到当前时刻Tracks的状态估计,并进行下一时刻的预测。针对点目标跟踪MATLAB提供了trackerGNN, trackerJPDA, trackerTOMHT实现上述框架算法,对应的Simulink模块如图2所示。可以直接在Simulink中如图3所示使用,输出即融合后的Tracks,后续可以再根据具体功能选择CIPV或ACC targets。
下面具体来看下各个组件与其关键属性,以及在MATLAB中如何定义:
1. 传感器融合输入Detections
即对应各传感器的目标探测信息,MATLAB通过System Object将Vision及Radar的探测Detections打包成为objectDetection,方便调试各种跟踪器及滤波器算法,其包括如图4所示属性:
a). Measurement,不论是通过实车测试,还是通过虚拟场景及传感器模型都可以得到Vision与Radar基于时间序列的探测对象数据,主要包括x/y位置信息,vx/vy速度信息。Radar也可能发出探测目标在极坐标系下的径向距离rng,水平及垂直角度az,el,径向速度rr。Vision输出的Detection都是针对单个目标的,Radar如果针对一个目标可输出多个Detections,则需要先进行聚类,如图3中 Detection Clustering模块所示。
b). MeasurementNoise,非常重要的参数,和传感器测量特性及状态矩阵相关的对角矩阵,直接影响到最后融合状态估计量更相信Vision还是Radar,以及是更相信测量值还是预测值。例如Rradar = diag([1,1,2,10]);Rvision = diag([2,2,1,10]);
c). MeasurementParameters,可用于存取各传感器坐标系与车辆坐标系转换的信息,最终输出的Detections以车辆坐标系为基准。
2. 多目标跟踪门Gating及数据关联 Assignment
在多目标跟踪中,为了减少不必要的数据关联计算,通过Tracks上一时刻状态预测当前时刻状态,建立当前时刻Tracks的有效跟踪门。利用门限来确定哪些Detections是Tracks的有效候选对象,在准确性可接受的范围内缩小门限值可加速数据关联。 由于传感器存在误报,漏报以及测量误差,同时也缺乏多目标环境的先验知识,可能多个Detections在同一个Track的门限内或者一个Detection在多个Tracks的门限内。如图6所示O1~O4是Detections,T1~T3是Tracks,因此需要数据关联将Vision及Radar的探测Detections分别与Tracks进行关联或新建Track。
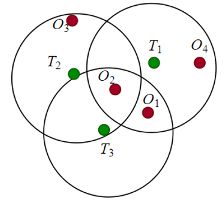
图6
图2中Simulink模块对应的数据关联算法即全局最近邻算法,联合概率数据关联,多假设跟踪数据关联。例如全局最近邻(GNN)数据关联算法:将门限内的一个Detection最多与一个Track关联,以使所有关联结果的总代价距离J最小。

图7
Cij表示Detection i与Track j之间的马氏距离,不同类别的探测目标(例如车辆和行人)之间,可以将其代价距离设置为较大值而不进行关联。对于2-D GNN分配问题,可以使用assignmunkres,assignauction,assignjv等算法进行求解。
3. 目标跟踪管理Track Maintenance
根据数据关联的结果,对有detections关联的tracks进行更新;将没有关联的探测Detections开始创建新的Tracks,且对假设性的Tracks进行更新确认;对没有Detections关联的Tracks进行没有更新的预测或删除。根据使用的关联算法可以选择不同的目标跟踪管理方法:trackerGNN和trackerJPDA可以使用基于历史数据的方法(History Logic)确认,例如某个Track在N次更新中,至少有M次更新分配了Detection,则可以确认。trackerGNN和trackerTOMHT可以基于打分的方法(Track Score Logic)进行确认。
4. 滤波器Filtering
虽然Vision和Radar可以对目标运动状态量进行测量,但由于噪声的存在,无法得到真值。实际项目中可以通过滤波对目标状态进行估计,尽量的逼近于真值。卡尔曼滤波根据状态方程和观测方程以递推的方式利用上一时刻的状态预测当前时刻的状态,并通过当前时刻的测量值对预测值进行更新得到当前时刻状态的最小方差估计。图7为卡尔曼滤波算法公式,是针对零均值高斯噪声的纯时域滤波器。那在MATLAB中如何根据下面公式创建一个卡尔曼滤波器?

步骤1:需定义目标运动模型及对应的状态转移矩阵F,如常见匀加速模型或机动模型。


步骤2:定义过程噪声Q, sigma为加速度变化率的最大值:

步骤3:定义测量模型矩阵H,结合Detections从各传感器获得的测量值和状态转移矩阵而定:


步骤4: 根据Detections输入状态和测量噪声确定目标初始状态及初始状态的协方差矩阵,每个时刻状态的不确定性都是通过状态协方差P矩阵(stateCov)来表示:

步骤5:结合步骤1~4创建滤波器初始化函数,用于新建track:

还可尝试更多滤波器:Alpha-Beta滤波/trackingABF, 卡尔曼/扩展卡尔曼/无迹卡尔曼/容积卡尔曼滤波/trackingKF/trackingEKF/trackingUKF/trackingCKF,高斯和滤波/trackingGSF,粒子滤波/trackingPF,交互多模式滤波/trackingIMM等。
完成上述各组件后就可创建用于多目标跟踪器trackerGNN / trackerJPDA / trackerTOMHT,例如:

最后,可以使用MATLAB创建的多目标跟踪器或Simulink模块,可以自动生成C/C++代码进行部署实现算法实时验证。
2022 年发布




