rcs
Calculate and plot monostatic and bistatic radar cross section (RCS) of platform, antenna, or array
Since R2019b
Syntax
Description
rcs(
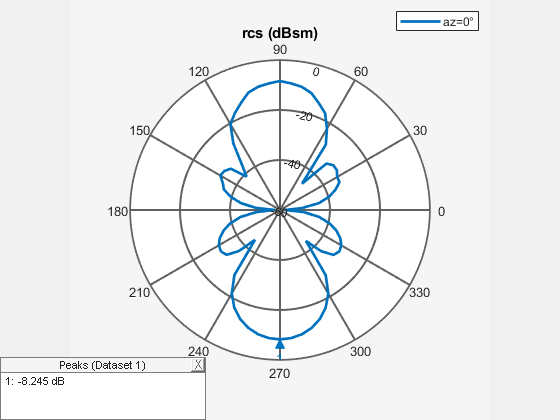
plots the monostatic RCS of the platform, antenna, or array over a specified frequency. To
learn more about monostatic and bistatic RCS, see What Is RCS?.object,frequency)
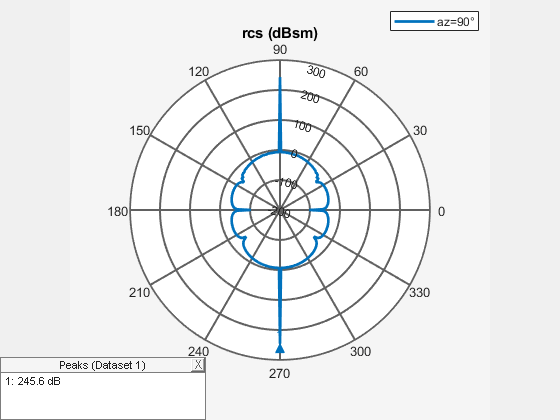
rcs(___, plots the
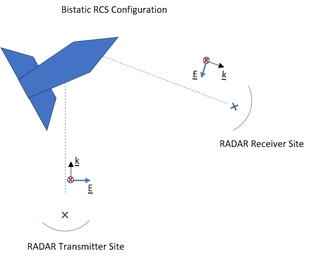
RCS with additional properties specified using one or more Name-Value Arguments. To plot a bistatic
RCS, specify the TransmitAngle name-value argument
as a 2-by-1 matrix with non-zero values.Name=Value)
[ returns the RCS value and
corresponding azimuth and elevation angles using additional properties specified by one or
more name-value arguments. To calculate a bistatic RCS, specify the TransmitAngle name-value argument
as a 2-by-1 matrix. with non-zero values.rcsval,azimuth,elevation]
= rcs(___,Name=Value)
Examples
Input Arguments
Output Arguments
More About
References
[1] Gurel, L., H. Bagrci, J. C. Castelli, A. Cheraly, F. Tardivel. "Validation Through Comparison: Measurement and Calculation of the Bistatic Radar Cross Section of a Stealth Target." Radio Science. Vol. 38, Number 3, 2003, pp.12-1 - 12-8.
[2] Rao, S.M., D. R. Wilton, A. W. Glisson. "Electromagnetic Scattering by Surfaces of Arbitrary Shape." IEEE Trans. Antennas and Propagation. Vol. AP-30, Number 3, 1982, pp.409-418.
[3] Jakobus, U., F. M. Landstorfer. "Improved PO-MM Formulation for Scattering from Three-Dimensional Perfectly Conducting Bodies of Arbitrary Shape.." IEEE Trans. Antennas and Propagation. Vol. AP-43, Number 2, 1995, pp.162-169.
Version History
Introduced in R2019b