Limited Slip Differential
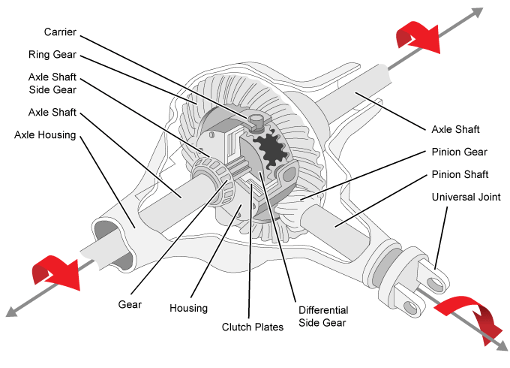
Limited differential as a planetary bevel gear
Libraries:
Powertrain Blockset /
Drivetrain /
Final Drive Unit
Vehicle Dynamics Blockset /
Powertrain /
Drivetrain /
Final Drive Unit
Description
The Limited Slip Differential block implements a differential as a planetary bevel gear train. The block matches the driveshaft bevel gear to the crown (ring) bevel gear. You can specify:
Carrier-to-driveshaft ratio
Crown wheel location
Viscous and damping coefficients for the axles and carrier
Type of slip coupling
Use the block in system-level driveline analysis to account for the power transfer from the transmission to the wheels. The block is suitable for use in hardware-in-the-loop (HIL) and optimization workflows. All the parameters are tunable.
In a limited slip differential, to prevent one of the wheels from slipping, the differential splits the torque applied to the left and right axles. With different torque applied to the axles, the wheels can move at different angular velocities, preventing slip. The block implements three methods for coupling the different torques applied to the axes:
Pre-loaded ideal clutch
Slip speed-dependent torque data
Input torque dependent torque data
The block uses a coordinate system that produces positive tire and vehicle motion for standard engine, transmission, and differential configurations. The arrows indicate positive motion.
Efficiency
To account for the block efficiency, use the Efficiency factors parameter. This table summarizes the block implementation for each setting.
| Setting | Implementation |
|---|---|
| Constant efficiency that you can set with the Constant efficiency factor, eta parameter. |
| Efficiency as a function of base gear input torque, air temperature, and driveshaft speed. Use these parameters to specify the lookup table and breakpoints:
For the air temperature, you can either:
To select the interpolation method, use the Interpolation method parameter. For more information, see Interpolation Methods. |
Power Accounting
For the power accounting, the block implements these equations.
| Bus Signal | Description | Equations | ||
|---|---|---|---|---|
|
|
| Mechanical power from driveshaft | |
| Mechanical power from axle 1 | |||
| Mechanical power from axle 2 | |||
|
|
| Total power loss | ||
| Power loss due to damping | |||
| Power loss due to clutch | |||
|
|
| Rate change of stored internal energy | ||
Dynamics
The Limited Slip Differential block implements these differential equations to represent the mechanical dynamic response for the crown gear, left axle, and right axle.
| Mechanical Dynamic Response | Differential Equation |
|---|---|
| Crown Gear |
|
| Left Axle |
|
| Right Axle |
|
The block assumes rigid coupling between the crown gear and axles. These constraint equations apply.
The equations use these variables.
| N | Carrier-to-driveshaft gear ratio |
| Jd | Rotational inertia of the crown gear assembly |
| bd | Crown gear linear viscous damping |
| ωd | Driveshaft angular speed |
Slip speed | |
| J1 | Axle 1 rotational inertia |
| b1 | Axle 1 linear viscous damping |
| ω1 | Axle 1 speed |
| J2 | Axle 2 rotational inertia |
| b2 | Axle 2 linear viscous damping |
| ω2 | Axle 2 angular speed |
| η | Efficiency |
| Td | Driveshaft torque |
| T1 | Axle 1 torque |
| T2 | Axle 2 torque |
| Ti | Axle internal resistance torque |
| Ti1 | Axle 1 internal resistance torque |
| Ti2 | Axle 2 internal resistance torque |
| μ | Coefficient of friction |
Effective clutch radius | |
Annular disk outer radius | |
| Ri | Annular disk inner radius |
| Fc | Clutch force |
| Tc | Clutch torque |
| μ | Coefficient of friction |
Table blocks in the Limited Slip Differential have these parameter settings:
Interpolation method —
LinearExtrapolation method —
Clip
The ideal clutch coupling model uses the axle slip speed and friction to calculate the clutch torque. The friction coefficient is a function of the slip speed.
The disc radii determine the effective clutch radius over which the clutch force acts.
The angular velocities of the axles determine the slip speed.
To calculate the clutch torque, the slip speed coupling model uses torque data that is a function of slip speed. The angular velocities of the axles determine the slip speed.
To calculate the clutch torque, the input torque coupling model uses torque data that is a function of input torque.
The Open Differential block assumes rigid coupling between the crown gear and axles. These constraint equations apply.
Ports
Inputs
Output
Parameters
References
[1] Deur, J., Ivanović, V., Hancock, M., and Assadian, F. "Modeling of Active Differential Dynamics." In ASME proceedings. Transportation Systems. Vol. 17, pp: 427-436.
Extended Capabilities
Version History
Introduced in R2017a