Calibrate ECMS Block for Objective Hybrid Vehicle Fuel Economy Assessment
Powertrain Blockset™ allows you to simulate the fuel economy, performance, and emissions of hybrid electric vehicles with standard hybrid powertrain architectures P0, P1, P2, P3, and P4. When you compare fuel economy changes in a hybrid vehicle drive cycle, you must account for the amount of energy stored in the vehicle battery. Otherwise, net battery charging or depletion during the drive cycle can artificially inflate or deflate the fuel economy estimate for the drive cycle.
Powertrain Blockset uses an industry-standard equivalent consumption minimization strategy (ECMS) to optimize the fuel economy of hybrid reference applications by optimally trading off internal combustion engine (ICE) use versus electric motor use during a given drive cycle.
This ECMS calibration script automatically optimizes the weighting factor parameter, ECMS_s. The script runs a drive-cycle simulation, measures starting and ending SOC, and repeats the process until the difference between starting and ending SOC is minimized.
During the optimization process, an optimization plot indicates the progress of the optimizer toward net zero change in SOC over the given driven cycle for the chosen vehicle configuration.
The optimization can take more than one hour to complete. After optimization completes, the ECMS_s parameter for net zero change in cycle SOC is stored in the Optimal Control Model Reference model workspace.

The Equivalent Consumption Minimization Strategy block in the hybrid controller of each hybrid reference application optimizes trading off engine and motor use during the cycle. The Equivalent Consumption Minimization Strategy block uses a weighting factor parameter, ECMS_s, that you can set so that the hybrid battery state of charge (SOC) at the end of a given drive cycle is the same as the SOC at the beginning of the drive cycle. The block optimizes fuel economy.

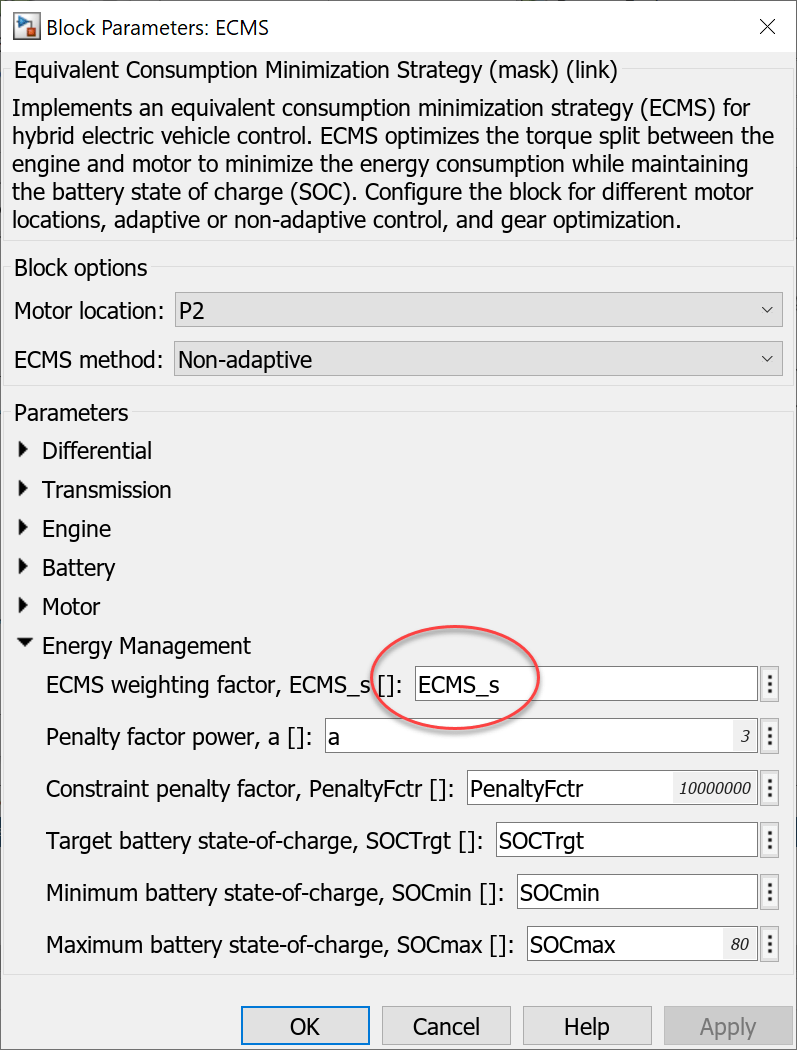
ECMS Calibration Script
Use this code to calibrate the ECMS_s block parameter for net zero change in battery SOC for any of the Powertrain Blockset Hybrid Reference Applications P0, P1, P2, P3, and P4.
First, choose the HEV reference application. This example uses the P2 reference application.
% Add example location to path exFld=pwd; addpath(exFld); % Open a given reference application pxName="P2"; % HEV powertrain architecture configuration: P0,P1,P2,P3,P4 eval("autoblkHev"+pxName+"Start"); %Start a Px Reference Application SOCinit = 0.6; % initial SOC, unit is in [0, 1]
Next, execute the optimization function Calibrate_ECMS_s.
As the optimization runs, you can view progress in the FTP75 Drive-Cycle SOC Balance plots. The plot showing the dSOC versus ECMS_s parameter value shows the difference between the optimized SOC and the actual SOC for each weighting factor. As the optimization converges, the difference approaches zero. The plot showing the SOC versus ECMS_s parameter value shows the actual SOC for each weighting factor.
ECMS_s=CalibrateECMSs(pxName,SOCinit);
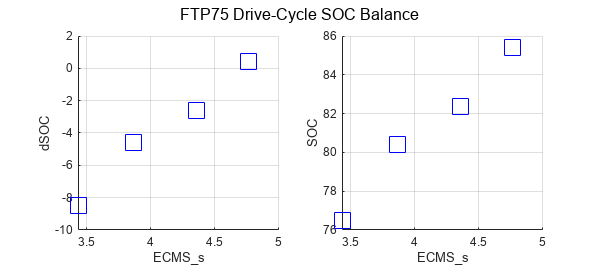
Elapsed time is 355.876638 seconds. Search converged. ECMS_s parameter updated in model. ECMS_s = 4.308011, SOCEndTrg = 60.000000, SOC_end = 60.000000
rmpath(exFld);
See Also
Equivalent Consumption Minimization Strategy