Mesures ACPR et CCDF avec MATLAB System objects
Mesures ACPR
Cet exemple montre comment mesurer le rapport de puissance du canal adjacent (ACPR, Adjacent Channel Power Ratio) d’une bande de base, de signal QPSK 50 kbps. L’ACPR est le rapport de la puissance du signal mesuré dans une bande de fréquence adjacente sur la puissance du même signal mesuré dans sa bande principale. Le nombre d’échantillons par symbole est défini à quatre.
Configurez les échantillons par symbole (sps) et les paramètres de la bande passante (bw) du canal.
sps = 4; bw = 50e3;
Générez 10 000 symboles 4-aires pour la modulation QPSK.
data = randi([0 3],10000,1);
Construisez un modulateur QPSK, puis modulez les données en entrée.
x = pskmod(data,4);
Appliquez des formes d’impulsions rectangulaires au signal modulé. Ce type de forme d’impulsion n’est généralement pas employé dans un système pratique, mais est utilisé ici à des fins d’illustration.
y = rectpulse(x,sps);
Construisez un System object ACPR. Le taux d'échantillonnage est la bande passante multipliée par le nombre d’échantillons par symbole. Le canal principal est présumé être à 0 tandis que le décalage du canal adjacent est réglé à 50 kHz (identique à la bande passante du canal principal). De la même manière, la mesure de la bande passante du canal adjacent est réglée pour être la même que le canal principal. Pour finir, activez les ports de sortie de puissance des canaux principal et adjacent.
acpr = comm.ACPR(SampleRate=bw*sps,... MainChannelFrequency=0,... MainMeasurementBandwidth=bw,... AdjacentChannelOffset=50e3,... AdjacentMeasurementBandwidth=bw,... MainChannelPowerOutputPort=true,... AdjacentChannelPowerOutputPort=true);
Mesurez l’ACPR, la puissance du canal principal et la puissance du canal adjacent du signal y.
[ACPRout,mainPower,adjPower] = acpr(y)
ACPRout = -9.3071
mainPower = 28.9389
adjPower = 19.6318
Changez le décalage de fréquence à 75 kHz et déterminez l’ACPR. La propriété AdjacentChannelOffset n’étant pas ajustable, il faut d’abord valider acpr. Observez que l’ACPR augmente quand le décalage de canal est augmenté.
release(acpr) acpr.AdjacentChannelOffset = 75e3; ACPRout = acpr(y)
ACPRout = -13.1702
Validez acpr et spécifiez un décalage de canal adjacent de 50 kHz.
release(acpr) acpr.AdjacentChannelOffset = 50e3;
Créez un filtre en cosinus surélevé et filtrez le signal modulé.
txfilter = comm.RaisedCosineTransmitFilter( ...
OutputSamplesPerSymbol=sps);
z = txfilter(x);Mesurez l’ACPR pour le signal filtré z. Vous pouvez voir que l’ACPR augmente entre -9,5 dB et -17,7 dB lorsque les impulsions en cosinus surélevé sont utilisées.
ACPRout = acpr(z)
ACPRout = -17.2245
Tracez les rapports de puissances du canal adjacent sur la plage de valeur des décalages des canaux adjacents. Configurez les plages de décalages du canal pour qu’ils varient de 30 kHz à 70 kHz par palier de 10 kHz. Ici encore, il faut d’abord valider hACPR pour modifier le décalage.
freqOffset = 1e3*(30:5:70); release(acpr) acpr.AdjacentChannelOffset = freqOffset;
Déterminez les valeurs ACPR pour les signaux avec des formes d'impulsion rectangulaires et en cosinus surélevé.
ACPR1 = acpr(y); ACPR2 = acpr(z);
Tracez les rapports de puissance du canal adjacent.
plot(freqOffset/1000,ACPR1,'*-',freqOffset/1000, ACPR2,'o-') xlabel('Adjacent Channel Offset (kHz)') ylabel('ACPR (dB)') legend('Rectangular','Raised Cosine','location','best') grid
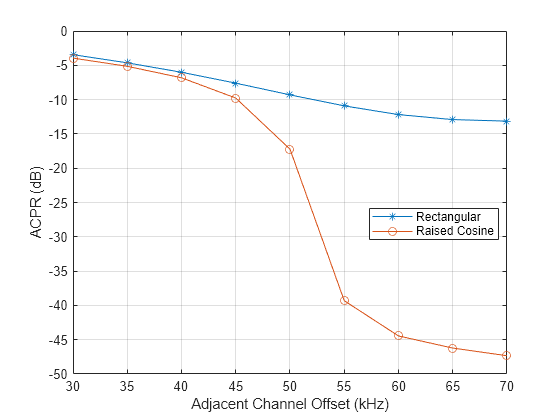
Mesures CCDF
Cet exemple montre comment utiliser le System object™ powermeter pour mesurer la probabilité que la puissance instantanée d’un signal soit supérieure à un niveau spécifié par rapport à sa puissance moyenne. Construisez un objet powermeter et définissez les propriétés Measurement et ComputeCCDF.
pm = powermeter(Measurement="Peak-to-average power ratio",ComputeCCDF=true);Définissez les paramètres OFDM.
fftLength = 256; cyclicPrefixLength = 32; nullIdx = [1:6 fftLength-4:fftLength]'; numFrames = 20; ofdmInputSize = fftLength - numel(nullIdx); ofdmOutputSize = fftLength + cyclicPrefixLength;
Générez les signaux 64-QAM et OFDM pour l'évaluation.
data = randi([0 63],ofdmInputSize,numFrames); % Apply 64-QAM modulation tmpQAM = qammod(data,64); % Save the signal data qamSig = tmpQAM(:); % Apply OFDM modulation to the QAM-modulated signal ofdmSig = ofdmmod(tmpQAM,fftLength,cyclicPrefixLength,nullIdx);
Déterminez les valeurs PAPR pour les deux signaux. Les deux signaux évalués doivent avoir la même longueur pour que les 4 000 premiers symboles soient évalués.
PAPR = pm([qamSig(1:4000),ofdmSig(1:4000)]);
Tracez les données CCDF. Prenez en compte que la probabilité que la puissance du signal modulé OFDM soit plus de 3 dB au dessus de sa puissance moyenne est beaucoup plus importante que pour le signal modulé QAM.
plotCCDF(pm) legend('QAM','OFDM','location','best')

Comparez les valeurs PAPR pour les signaux modulés QAM et AFDM.
fprintf('\nPAPR for 64-QAM = %5.2f dB\nPAPR for OFDM = %5.2f dB\n',... PAPR(1), PAPR(2))
PAPR for 64-QAM = 3.65 dB PAPR for OFDM = 9.44 dB
Il est possible de voir qu’en appliquant la modulation AFDM à un signal modulé 64-QAM, le PAPR augmente de 5,8 dB. Cela signifie que si une puissance d'émission de 30 dBm est nécessaire pour fermer un lien 64-QAM, l’amplificateur de puissance doit avoir une puissance maximale de 33,7 dBm afin d’assurer une opération linéaire. Si le même signal était alors modulé OFDM, un amplificateur de puissance de 39,5 dBm serait requis.