Detect ARCH Effects Using Econometric Modeler App
These examples show how to assess whether a series has volatility clustering by using
the Econometric Modeler app. Methods include inspecting correlograms of
squared residuals and testing for significant ARCH lags. The data set, stored in
Data_EquityIdx.mat, contains a series of daily NASDAQ closing
prices from 1990 through 2001.
Inspect Correlograms of Squared Residuals for ARCH Effects
This example shows how to visually determine whether a series has significant ARCH effects by plotting the autocorrelation function (ACF) and partial autocorrelation function (PACF) of a series of squared residuals.
At the command line, load the Data_EquityIdx.mat data
set.
load Data_EquityIdxThe data set contains a table of NASDAQ and NYSE closing prices, among
other variables. For more details about the data set, enter
Description at the command line.
At the command line, open the Econometric Modeler app.
econometricModeler
Alternatively, open the app from the apps gallery (see Econometric Modeler).
Import DataTimeTable into the app:
On the Econometric Modeler tab, in the Import section, click the Import button
 .
.In the Import Data dialog box, in the Import? column, select the check box for the
DataTimeTablevariable.Click Import.
The variables appear in the Time Series pane, and a time series plot of all the series appears in the Time Series Plot(NASDAQ) figure window.
Convert the daily close NASDAQ index series to a percentage return series by taking the log of the series, then taking the first difference of the logged series:
In the Time Series pane, select
NASDAQ.On the Econometric Modeler tab, in the Transforms section, click Log.
With
NASDAQLogselected, in the Transforms section, click Difference.In the Time Series pane, rename the
NASDAQLogDiffvariable by clicking it twice to select its name and enteringNASDAQReturns.
The time series plot of the NASDAQ returns appears in the Time Series Plot(NASDAQReturns) figure window.

The returns appear to fluctuate around a constant level, but exhibit volatility clustering. Large changes in the returns tend to cluster together, and small changes tend to cluster together. That is, the series exhibits conditional heteroscedasticity.
Compute squared residuals:
Export
NASDAQReturnsto the MATLAB® Workspace:In the Time Series pane, right-click
NASDAQReturns.In the context menu, select Export.
NASDAQReturnsappears in the MATLAB Workspace.At the command line:
For numerical stability, scale the returns by a factor of 100.
Create a residual series by removing the mean from the scaled returns series. Because you took the first difference of the NASDAQ prices to create the returns, the first element of the returns is missing. Therefore, to estimate the sample mean of the series, call
mean(NASDAQReturns,'omitnan').Square the residuals.
Add the squared residuals as a new variable to the
DataTimeTabletimetable.
NASDAQReturns = 100*NASDAQReturns; NASDAQResiduals = NASDAQReturns - mean(NASDAQReturns,'omitnan'); NASDAQResiduals2 = NASDAQResiduals.^2; DataTimeTable.NASDAQResiduals2 = NASDAQResiduals2;
In Econometric Modeler, import DataTimeTable:
On the Econometric Modeler tab, in the Import section, click
 .
.In the Econometric Modeler dialog box, click OK to clear all variables and documents in the app.
In the Import Data dialog box, in the Import? column, select the check box for
DataTimeTable.Click Import.
Plot the ACF and PACF:
In the Time Series pane, select the
NASDAQResiduals2time series.Click the Plots tab, then click ACF.
Click the Plots tab, then click PACF.
Close the Time Series Plot(NASDAQ) figure window. Then, position the ACF(NASDAQResiduals2) figure window above the PACF(NASDAQResiduals2) figure window.
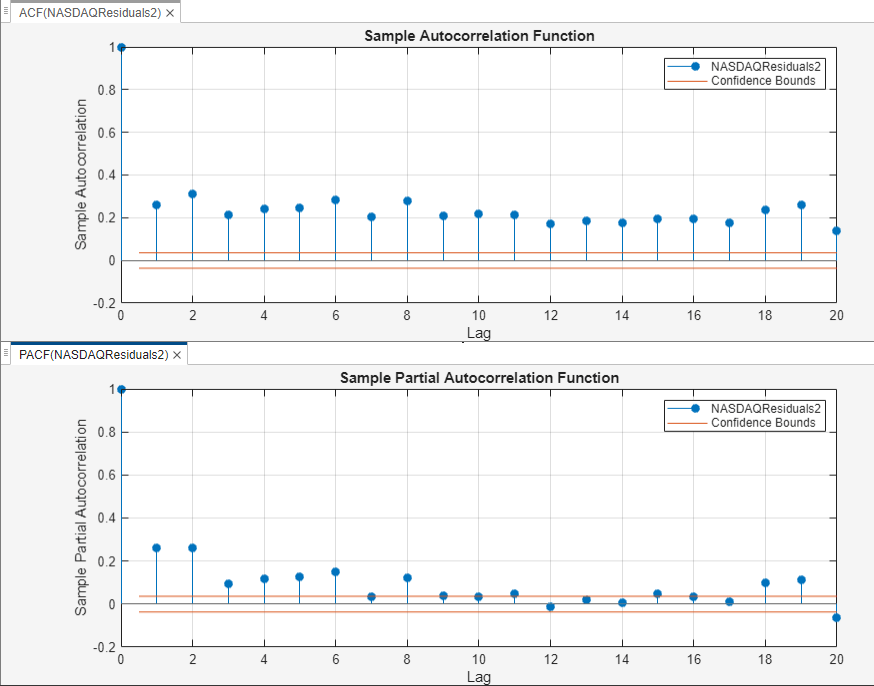
The sample ACF and PACF show significant autocorrelation in the squared residuals. This result indicates that volatility clustering is present.
Conduct Ljung-Box Q-Test on Squared Residuals
This example shows how to test squared residuals for significant ARCH effects using the Ljung-Box Q-test.
At the command line:
Load the
Data_EquityIdx.matdata set.Convert the NASDAQ prices to returns. To maintain the correct time base, prepend the resulting returns with a
NaNvalue.Scale the NASDAQ returns.
Compute residuals by removing the mean from the scaled returns.
Square the residuals.
Add the vector of squared residuals as a variable to
DataTimeTable.
For more details on the steps, see Inspect Correlograms of Squared Residuals for ARCH Effects.
load Data_EquityIdx NASDAQReturns = 100*price2ret(DataTimeTable.NASDAQ); NASDAQReturns = [NaN; NASDAQReturns]; NASDAQResiduals2 = (NASDAQReturns - mean(NASDAQReturns,'omitnan')).^2; DataTimeTable.NASDAQResiduals2 = NASDAQResiduals2;
At the command line, open the Econometric Modeler app.
econometricModeler
Alternatively, open the app from the apps gallery (see Econometric Modeler).
Import DataTimeTable into the app:
On the Econometric Modeler tab, in the Import section, click the Import button
 .
.In the Import Data dialog box, in the Import? column, select the check box for the
DataTimeTablevariable.Click Import.
The variables appear in the Time Series pane, and a time series plot of all the series appears in the Time Series Plot(NASDAQ) figure window.
Test the null hypothesis that the first m = 5 autocorrelation lags of the squared residuals are jointly zero by using the Ljung-Box Q-test. Then, test the null hypothesis that the first m = 10 autocorrelation lags of the squared residuals are jointly zero.
In the Time Series pane, select the
NASDAQResiduals2time series.On the Econometric Modeler tab, in the Tests section, click New Test > Ljung-Box Q-Test.
On the LBQ tab, in the Parameters section, set both the Number of Lags and DOF to
5. To maintain a significance level of 0.05 for the two tests, set Significance Level to 0.025.In the Tests section, click Run Test.
Repeat steps 3 and 4, but set both the Number of Lags and DOF to
10instead.
The test results appear in the Results table of the LBQ(NASDAQResiduals2) document.

The null hypothesis is rejected for the two tests. The p-value for each test is 0. The results show that not every autocorrelation up to lag 5 (or 10) is zero, indicating volatility clustering in the squared residuals.
Conduct Engle's ARCH Test
This example shows how to test residuals for significant ARCH effects using the Engle's ARCH Test.
At the command line:
Load the
Data_EquityIdx.matdata set.Convert the NASDAQ prices to returns. To maintain the correct time base, prepend the resulting returns with a
NaNvalue.Scale the NASDAQ returns.
Compute residuals by removing the mean from the scaled returns.
Add the vector of residuals as a variable to
DataTimeTable.
For more details on the steps, see Inspect Correlograms of Squared Residuals for ARCH Effects.
load Data_EquityIdx NASDAQReturns = 100*price2ret(DataTimeTable.NASDAQ); NASDAQReturns = [NaN; NASDAQReturns]; NASDAQResiduals = NASDAQReturns - mean(NASDAQReturns,'omitnan'); DataTimeTable.NASDAQResiduals = NASDAQResiduals;
At the command line, open the Econometric Modeler app.
econometricModeler
Alternatively, open the app from the apps gallery (see Econometric Modeler).
Import DataTimeTable into the app:
On the Econometric Modeler tab, in the Import section, click the Import button
 .
.In the Import Data dialog box, in the Import? column, select the check box for the
DataTimeTablevariable.Click Import.
The variables appear in the Time Series pane, and a time series plot of the all the series appears in the Time Series Plot(NASDAQ) figure window.
Test the null hypothesis that the NASDAQ residuals series exhibits no ARCH effects by using Engle's ARCH test. Specify that the residuals series is an ARCH(2) model.
In the Time Series pane, select the
NASDAQResidualstime series.On the Econometric Modeler tab, in the Tests section, click New Test > Engle's ARCH Test.
On the ARCH tab, in the Parameters section, set Number of Lags to
2.In the Tests section, click Run Test.
The test results appear in the Results table of the ARCH(NASDAQResiduals) document.

The null hypothesis is rejected in favor of the ARCH(2) alternative. The test result indicates significant volatility clustering in the residuals.