Convert Neural Network Algorithms to Fixed-Point Using fxpopt and Generate HDL Code
This example shows how to convert a neural network regression model in Simulink® to fixed point using the fxpopt function and Lookup Table Optimizer.
Overview
Fixed-Point Designer™ provides workflows via the Fixed Point Tool that can convert a design from floating-point data types to fixed-point data types. The fxpopt function optimizes data types in a model based on specified system behavioral constraints. The Lookup Table Optimizer generates memory-efficient lookup table replacements for unbounded functions such as exp and log2. Using these tools, this example showcases how to convert a trained floating-point neural network regression model to use embedded-efficient fixed-point data types.
Data and Neural Network Training
The engine_dataset contains data representing the relationship between the fuel rate and speed of the engine, and its torque and gas emissions.
Use the Neural Net Fitting app (nftool) from Deep Learning Toolbox™ to train a neural network to estimate torque and gas emissions of an engine given the fuel rate and speed. Use the following commands to train the neural network.
load engine_dataset;
x = engineInputs;
t = engineTargets;
net = fitnet(10);
net = train(net,x,t);
view(net)


Close the view of the network.
nnet.guis.closeAllViews();
Model Preparation for Fixed-Point Conversion
Once the network is trained, use the gensim function from the Deep Learning Toolbox to generate a Simulink model.
[sysName, netName] = gensim(net, 'Name', 'mTrainedNN');

The model generated by the gensim function contains the neural network with trained weights and biases. To prepare this generated model for fixed-point conversion, follow the preparation steps in the best practices guidelines.
After applying these principles, the trained neural network is further modified to enable signal logging at the output of the network, add input stimuli and verification blocks.
Open and inspect the model. The model is already configured for HDL compatibility by using the hdlsetup function.
model = 'ex_fxpdemo_neuralnet_regression_hdlsetup'; system_under_design = [model '/Function Fitting Neural Network']; baseline_output = [model '/yarr']; open_system(model);

Simulate the model to observe model performance when using double-precision floating-point data types.
loggingInfo = get_param(model, 'DataLoggingOverride'); sim_out = sim(model, 'SaveFormat', 'Dataset'); plotRegression(sim_out, baseline_output, system_under_design, 'Regression before conversion');

Define System Behavioral Constraints for Fixed Point Conversion
opts = fxpOptimizationOptions(); opts.addTolerance(system_under_design, 1, 'RelTol', 0.05); opts.addTolerance(system_under_design, 1, 'AbsTol', 50) opts.AllowableWordLengths = 8:32;
Optimize Data Types
Use the fxpopt function to optimize the data types in the system under design and explore the solution. The software analyzes the range of objects in system_under_design and wordlength and tolerance constraints specified in opts to apply heterogeneous data types to the model while minimizing total bit width.
solution = fxpopt(model, system_under_design, opts); best_solution = solution.explore;
+ Starting data type optimization...
+ Checking for unsupported constructs.
- The paths printed in the Command Window have constructs that do not support fixed-point data types. These constructs will be surrounded with Data Type Conversion blocks.
'ex_fxpdemo_neuralnet_regression_hdlsetup/Function Fitting Neural Network/Layer 1/tansig/tanh'
+ Preprocessing
+ Modeling the optimization problem
- Constructing decision variables
+ Running the optimization solver
Exporting logged dataset prior to deleting run...done.
- Evaluating new solution: cost 515, does not meet the behavioral constraints.
- Evaluating new solution: cost 577, does not meet the behavioral constraints.
- Evaluating new solution: cost 639, does not meet the behavioral constraints.
- Evaluating new solution: cost 701, does not meet the behavioral constraints.
- Evaluating new solution: cost 763, does not meet the behavioral constraints.
- Evaluating new solution: cost 825, does not meet the behavioral constraints.
- Evaluating new solution: cost 887, does not meet the behavioral constraints.
- Evaluating new solution: cost 949, meets the behavioral constraints.
- Updated best found solution, cost: 949
- Evaluating new solution: cost 945, meets the behavioral constraints.
- Updated best found solution, cost: 945
- Evaluating new solution: cost 944, meets the behavioral constraints.
- Updated best found solution, cost: 944
- Evaluating new solution: cost 943, meets the behavioral constraints.
- Updated best found solution, cost: 943
- Evaluating new solution: cost 942, meets the behavioral constraints.
- Updated best found solution, cost: 942
- Evaluating new solution: cost 941, meets the behavioral constraints.
- Updated best found solution, cost: 941
- Evaluating new solution: cost 940, meets the behavioral constraints.
- Updated best found solution, cost: 940
- Evaluating new solution: cost 939, meets the behavioral constraints.
- Updated best found solution, cost: 939
- Evaluating new solution: cost 938, meets the behavioral constraints.
- Updated best found solution, cost: 938
- Evaluating new solution: cost 937, meets the behavioral constraints.
- Updated best found solution, cost: 937
- Evaluating new solution: cost 936, meets the behavioral constraints.
- Updated best found solution, cost: 936
- Evaluating new solution: cost 926, meets the behavioral constraints.
- Updated best found solution, cost: 926
- Evaluating new solution: cost 925, meets the behavioral constraints.
- Updated best found solution, cost: 925
- Evaluating new solution: cost 924, meets the behavioral constraints.
- Updated best found solution, cost: 924
- Evaluating new solution: cost 923, meets the behavioral constraints.
- Updated best found solution, cost: 923
- Evaluating new solution: cost 922, meets the behavioral constraints.
- Updated best found solution, cost: 922
- Evaluating new solution: cost 917, meets the behavioral constraints.
- Updated best found solution, cost: 917
- Evaluating new solution: cost 916, meets the behavioral constraints.
- Updated best found solution, cost: 916
- Evaluating new solution: cost 914, meets the behavioral constraints.
- Updated best found solution, cost: 914
- Evaluating new solution: cost 909, meets the behavioral constraints.
- Updated best found solution, cost: 909
- Evaluating new solution: cost 908, meets the behavioral constraints.
- Updated best found solution, cost: 908
- Evaluating new solution: cost 906, meets the behavioral constraints.
- Updated best found solution, cost: 906
- Evaluating new solution: cost 898, meets the behavioral constraints.
- Updated best found solution, cost: 898
- Evaluating new solution: cost 897, meets the behavioral constraints.
- Updated best found solution, cost: 897
- Evaluating new solution: cost 893, does not meet the behavioral constraints.
- Evaluating new solution: cost 896, meets the behavioral constraints.
- Updated best found solution, cost: 896
- Evaluating new solution: cost 895, meets the behavioral constraints.
- Updated best found solution, cost: 895
- Evaluating new solution: cost 894, meets the behavioral constraints.
- Updated best found solution, cost: 894
- Evaluating new solution: cost 893, meets the behavioral constraints.
- Updated best found solution, cost: 893
- Evaluating new solution: cost 892, meets the behavioral constraints.
- Updated best found solution, cost: 892
- Evaluating new solution: cost 891, meets the behavioral constraints.
- Updated best found solution, cost: 891
- Evaluating new solution: cost 890, meets the behavioral constraints.
- Updated best found solution, cost: 890
- Evaluating new solution: cost 889, meets the behavioral constraints.
- Updated best found solution, cost: 889
- Evaluating new solution: cost 888, meets the behavioral constraints.
- Updated best found solution, cost: 888
- Evaluating new solution: cost 878, meets the behavioral constraints.
- Updated best found solution, cost: 878
- Evaluating new solution: cost 877, meets the behavioral constraints.
- Updated best found solution, cost: 877
- Evaluating new solution: cost 876, meets the behavioral constraints.
- Updated best found solution, cost: 876
- Evaluating new solution: cost 875, meets the behavioral constraints.
- Updated best found solution, cost: 875
- Evaluating new solution: cost 874, meets the behavioral constraints.
- Updated best found solution, cost: 874
- Evaluating new solution: cost 869, meets the behavioral constraints.
- Updated best found solution, cost: 869
- Evaluating new solution: cost 868, does not meet the behavioral constraints.
- Evaluating new solution: cost 867, meets the behavioral constraints.
- Updated best found solution, cost: 867
- Evaluating new solution: cost 862, does not meet the behavioral constraints.
- Evaluating new solution: cost 866, does not meet the behavioral constraints.
- Evaluating new solution: cost 865, does not meet the behavioral constraints.
+ Optimization has finished.
- Neighborhood search complete.
- Maximum number of iterations completed.
+ Fixed-point implementation that satisfies the behavioral constraints found. The best found solution is applied on the model.
- Total cost: 867
- Maximum absolute difference: 49.714162
- Use the explore method of the result to explore the implementation.
Verify model accuracy after conversion by simulating the model.
set_param(model, 'DataLoggingOverride', loggingInfo); Simulink.sdi.markSignalForStreaming([model '/yarr'], 1, 'on'); Simulink.sdi.markSignalForStreaming([model '/diff'], 1, 'on'); sim_out = sim(model, 'SaveFormat', 'Dataset');
Plot the regression accuracy of the fixed-point model.
plotRegression(sim_out, baseline_output, system_under_design, 'Regression after conversion');

Replace Activation Function with an Optimized Lookup Table
The Tanh Activation function in Layer 1 can be replaced with either a lookup table or a CORDIC implementation for more efficient fixed-point code generation. In this example, we will be using the Lookup Table Optimizer to get a lookup table as a replacement for tanh. We will be using EvenPow2Spacing for faster execution speed.
block_path = [system_under_design '/Layer 1/tansig']; p = FunctionApproximation.Problem(block_path); p.Options.WordLengths = 8:32; p.Options.BreakpointSpecification = 'EvenPow2Spacing'; solution = p.solve; solution.replaceWithApproximate;
Searching for fixed-point solutions. | ID | Memory (bits) | Feasible | Table Size | Breakpoints WLs | TableData WL | BreakpointSpecification | Error(Max,Current) | | 0 | 44 | 0 | 2 | 14 | 8 | EvenPow2Spacing | 7.812500e-03, 1.000000e+00 | | 1 | 4124 | 1 | 512 | 14 | 8 | EvenPow2Spacing | 7.812500e-03, 7.812500e-03 | | 2 | 4114 | 1 | 512 | 9 | 8 | EvenPow2Spacing | 7.812500e-03, 7.812500e-03 | | 3 | 2076 | 0 | 256 | 14 | 8 | EvenPow2Spacing | 7.812500e-03, 1.831055e-02 | | 4 | 2064 | 0 | 256 | 8 | 8 | EvenPow2Spacing | 7.812500e-03, 1.831055e-02 | | 5 | 46 | 0 | 2 | 14 | 9 | EvenPow2Spacing | 7.812500e-03, 1.000000e+00 | | 6 | 2332 | 0 | 256 | 14 | 9 | EvenPow2Spacing | 7.812500e-03, 2.563477e-02 | | 7 | 2320 | 0 | 256 | 8 | 9 | EvenPow2Spacing | 7.812500e-03, 2.563477e-02 | | 8 | 48 | 0 | 2 | 14 | 10 | EvenPow2Spacing | 7.812500e-03, 1.000000e+00 | | 9 | 2588 | 0 | 256 | 14 | 10 | EvenPow2Spacing | 7.812500e-03, 2.416992e-02 | | 10 | 2576 | 0 | 256 | 8 | 10 | EvenPow2Spacing | 7.812500e-03, 2.416992e-02 | | 11 | 50 | 0 | 2 | 14 | 11 | EvenPow2Spacing | 7.812500e-03, 1.000000e+00 | | 12 | 2844 | 0 | 256 | 14 | 11 | EvenPow2Spacing | 7.812500e-03, 2.319336e-02 | | 13 | 2832 | 0 | 256 | 8 | 11 | EvenPow2Spacing | 7.812500e-03, 2.319336e-02 | | 14 | 52 | 0 | 2 | 14 | 12 | EvenPow2Spacing | 7.812500e-03, 1.000000e+00 | | 15 | 3100 | 0 | 256 | 14 | 12 | EvenPow2Spacing | 7.812500e-03, 2.319336e-02 | | 16 | 3088 | 0 | 256 | 8 | 12 | EvenPow2Spacing | 7.812500e-03, 2.319336e-02 | | 17 | 54 | 0 | 2 | 14 | 13 | EvenPow2Spacing | 7.812500e-03, 1.000000e+00 | | 18 | 3356 | 0 | 256 | 14 | 13 | EvenPow2Spacing | 7.812500e-03, 2.343750e-02 | | 19 | 3344 | 0 | 256 | 8 | 13 | EvenPow2Spacing | 7.812500e-03, 2.343750e-02 | Best Solution | ID | Memory (bits) | Feasible | Table Size | Breakpoints WLs | TableData WL | BreakpointSpecification | Error(Max,Current) | | 2 | 4114 | 1 | 512 | 9 | 8 | EvenPow2Spacing | 7.812500e-03, 7.812500e-03 |
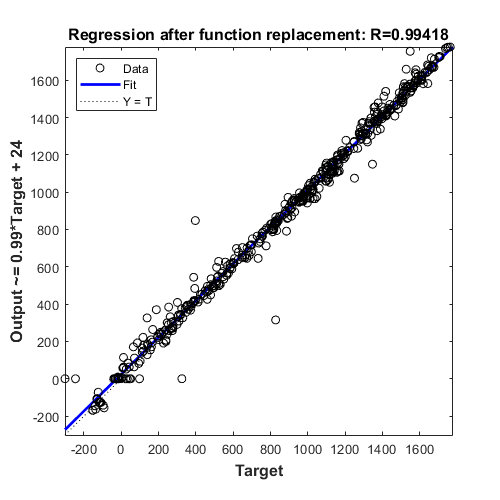
Verify model accuracy after function replacement
sim_out = sim(model, 'SaveFormat', 'Dataset');
Plot regression accuracy after function replacement.
plotRegression(sim_out, baseline_output, system_under_design, 'Regression after function replacement');
Generate HDL Code and Test Bench
Generating HDL code requires an HDL Coder™ license.
Choose the model for which to generate HDL code and a test bench.
systemname = 'ex_fxpdemo_neuralnet_regression/Function Fitting Neural Network';
Use a temporary directory for the generated files.
workingdir = tempname;
You can run the following command to check for HDL code generation compatibility.
checkhdl(systemname,'TargetDirectory',workingdir);
Run the following command to generate HDL code.
makehdl(systemname,'TargetDirectory',workingdir);
Run the following command to generate the test bench.
makehdltb(systemname,'TargetDirectory',workingdir);
See Also
fxpopt | FunctionApproximation.Options | Best Practices for Fixed-Point Conversion Workflow