Réalisation d'une optimisation multi-objectifs à l'aide de l'algorithme génétique
Cet exemple montre comment effectuer une optimisation multi-objectif à l'aide de la fonction d'algorithme génétique multi-objectif gamultiobj dans Global Optimization Toolbox.
Problème d'optimisation multi-objectif simple
gamultiobj peut être utilisé pour résoudre un problème d'optimisation multiobjectif dans plusieurs variables. Ici, nous voulons minimiser deux objectifs, chacun ayant une variable de décision.
min F(x) = [objective1(x); objective2(x)]
x where, objective1(x) = (x+2)^2 - 10, and
objective2(x) = (x-2)^2 + 20% Plot two objective functions on the same axis x = -10:0.5:10; f1 = (x+2).^2 - 10; f2 = (x-2).^2 + 20; plot(x,f1); hold on; plot(x,f2,'r'); grid on; title('Plot of objectives ''(x+2)^2 - 10'' and ''(x-2)^2 + 20''');
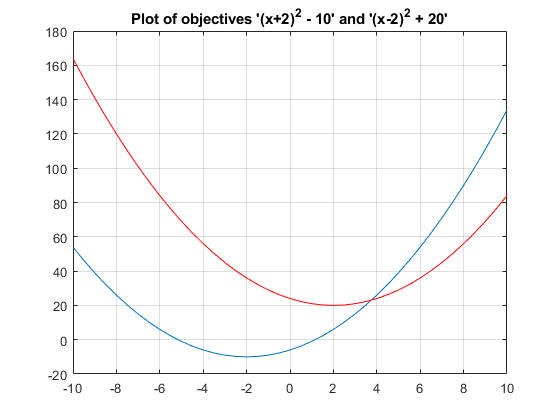
Les deux objectifs ont leurs minima à x = -2 et x = +2 respectivement. Cependant, dans un problème multiobjectif, x = -2, x = 2 et toute solution dans la plage -2 <= x <= 2 sont également optimales. Il n’existe pas de solution unique à ce problème multi-objectifs. L’objectif de l’algorithme génétique multiobjectif est de trouver un ensemble de solutions dans cette plage (idéalement avec une bonne répartition). L'ensemble des solutions est également connu sous le nom de front de Pareto. Toutes les solutions du front de Pareto sont optimales.
Codage de la fonction fitness
Nous créons un fichier MATLAB ® nommé simple_multiobjective.m :
function y = simple_multiobjective(x) y(1) = (x+2)^2 - 10; y(2) = (x-2)^2 + 20;
Le solveur d'algorithme génétique suppose que la fonction fitness prendra une entrée x, où x est un vecteur de lignes avec autant d'éléments que le nombre de variables dans le problème. La fonction fitness calcule la valeur de chaque fonction objectif et renvoie ces valeurs dans une seule sortie vectorielle y.
Minimiser en utilisant gamultiobj
Pour utiliser la fonction gamultiobj, nous devons fournir au moins deux arguments en entrée, une fonction fitness et le nombre de variables dans le problème. Les deux premiers arguments de sortie renvoyés par gamultiobj sont X, les points sur le front de Pareto, et FVAL, les valeurs de la fonction objectif aux valeurs X. Un troisième argument de sortie, exitFlag, vous indique la raison pour laquelle gamultiobj s'est arrêté. Un quatrième argument, OUTPUT, contient des informations sur les performances du solveur. gamultiobj peut également renvoyer un cinquième argument, POPULATION, qui contient la population lorsque gamultiobj est terminé et un sixième argument, SCORE, qui contient les valeurs de fonction de tous les objectifs pour POPULATION lorsque gamultiobj est terminé.
FitnessFunction = @simple_multiobjective; numberOfVariables = 1; [x,fval] = gamultiobj(FitnessFunction,numberOfVariables);
gamultiobj stopped because it exceeded options.MaxGenerations.
Le X renvoyé par le solveur est une matrice dans laquelle chaque ligne est le point sur le front de Pareto pour les fonctions objectif. Le FVAL est une matrice dans laquelle chaque ligne contient la valeur des fonctions objectif évaluées au point correspondant dans X.
size(x) size(fval)
ans =
18 1
ans =
18 2
Problème d'optimisation multi-objectifs sous contraintes
gamultiobj peut gérer les problèmes d'optimisation avec des contraintes d'inégalité linéaire, d'égalité et bornées simples. Ici, nous souhaitons ajouter des contraintes bornées sur un problème multi-objectif simple résolu précédemment.
min F(x) = [objective1(x); objective2(x)]
xsubject to -1.5 <= x <= 0 (bound constraints)
where, objective1(x) = (x+2)^2 - 10, and
objective2(x) = (x-2)^2 + 20 gamultiobj accepte les contraintes d'inégalité linéaire sous la forme A*x <= b et les contraintes d'égalité linéaire sous la forme Aeq*x = beq et les contraintes bornées sous la forme lb <= x <= ub. Nous passons A et Aeq comme matrices et b, beq, lb et ub comme vecteurs. Comme nous n’avons aucune contrainte linéaire dans cet exemple, nous transmettons [] pour ces entrées.
A = []; b = []; Aeq = []; beq = []; lb = -1.5; ub = 0; x = gamultiobj(FitnessFunction,numberOfVariables,A,b,Aeq,beq,lb,ub);
gamultiobj stopped because it exceeded options.MaxGenerations.
Toutes les solutions dans X (chaque ligne) satisferont toutes les contraintes linéaires et bornées dans la tolérance spécifiée dans options.ConstraintTolerance. Cependant, si vous utilisez votre propre fonction de croisement ou de mutation, assurez-vous que les nouveaux individus sont réalisables par rapport aux contraintes linéaires et aux contraintes bornées simples.
Ajouter des visualisations
gamultiobj peut accepter une ou plusieurs fonctions de tracé via l'argument options. Cette fonctionnalité est utile pour visualiser les performances du solveur au moment de l'exécution. Les fonctions de tracé peuvent être sélectionnées à l'aide de optimoptions.
Ici, nous utilisons optimoptions pour sélectionner deux fonctions de tracé. La première fonction de tracé est gaplotpareto, qui trace le front de Pareto (limité à trois objectifs) à chaque génération. La deuxième fonction de tracé est gaplotscorediversity, qui trace la diversité des scores pour chaque objectif. Les options sont passées comme dernier argument au solveur.
options = optimoptions(@gamultiobj,'PlotFcn',{@gaplotpareto,@gaplotscorediversity});
gamultiobj(FitnessFunction,numberOfVariables,[],[],[],[],lb,ub,options);
gamultiobj stopped because it exceeded options.MaxGenerations.
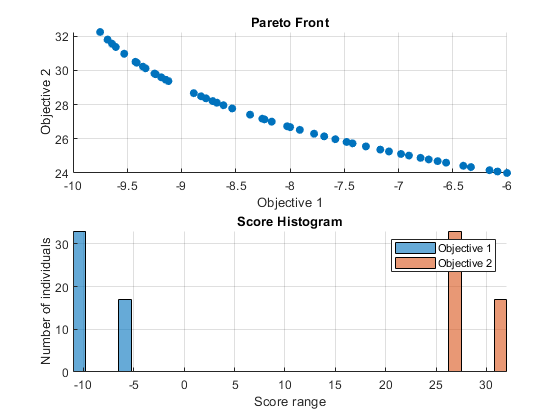
Vectorisation de votre fonction fitness
Considérez à nouveau les fonctions fitness précédentes :
objective1(x) = (x+2)^2 - 10, and objective2(x) = (x-2)^2 + 20
Par défaut, le solveur gamultiobj ne transmet qu'un seul point à la fois à la fonction fitness. Cependant, si la fonction fitness est vectorisée pour accepter un ensemble de points et renvoie un ensemble de valeurs de fonction, vous pouvez accélérer votre solution.
Par exemple, si le solveur doit évaluer cinq points en un seul appel à cette fonction fitness, il appellera la fonction avec une matrice de taille 5 par 1, c'est-à-dire 5 lignes et 1 colonne (rappelons que 1 est le nombre de variables).
Créez un fichier MATLAB appelé vectorized_multiobjective.m :
function scores = vectorized_multiobjective(pop)
popSize = size(pop,1); % Population size
numObj = 2; % Number of objectives
% initialize scores
scores = zeros(popSize, numObj);
% Compute first objective
scores(:,1) = (pop + 2).^2 - 10;
% Compute second objective
scores(:,2) = (pop - 2).^2 + 20;Cette version vectorisée de la fonction fitness prend une matrice pop avec un nombre arbitraire de points, les lignes de pop, et renvoie une matrice de taille populationSize par numberOfObjectives.
Nous devons spécifier que la fonction fitness est vectorisée à l'aide des options créées à l'aide de optimoptions. Les options sont transmises en tant que neuvième argument.
FitnessFunction = @(x) vectorized_multiobjective(x);
options = optimoptions(@gamultiobj,'UseVectorized',true);
gamultiobj(FitnessFunction,numberOfVariables,[],[],[],[],lb,ub,options);
gamultiobj stopped because the average change in the spread of Pareto solutions is less than options.FunctionTolerance.