Optimiser à l'aide d'un essaim particulaire
Cet exemple montre comment optimiser à l'aide du solveur particleswarm.
La fonction objectif dans cet exemple est la cinquième fonction de De Jong, qui est disponible lorsque vous exécutez cet exemple.
dejong5fcn
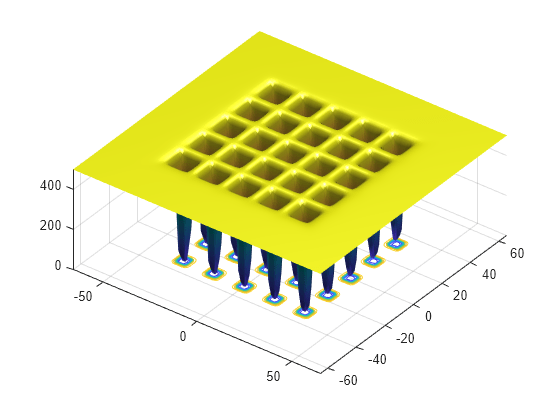
Cette fonction possède 25 minimums locaux.
Essayez de trouver le minimum de la fonction en utilisant les paramètres par défaut particleswarm.
fun = @dejong5fcn; nvars = 2; rng default % For reproducibility [x,fval,exitflag] = particleswarm(fun,nvars)
Optimization ended: relative change in the objective value over the last OPTIONS.MaxStallIterations iterations is less than OPTIONS.FunctionTolerance.
x = 1×2
-31.9521 -16.0176
fval = 5.9288
exitflag = 1
La solution x est-elle l’optimum global ? Ce n'est pas clair à ce stade. L'examen du graphique de la fonction montre que la fonction a des minima locaux pour les composants dans la plage [-50,50]. Ainsi, restreindre la plage des variables à [-50,50] aide le solveur à localiser un minimum global.
lb = [-50;-50]; ub = -lb; [x,fval,exitflag] = particleswarm(fun,nvars,lb,ub)
Optimization ended: relative change in the objective value over the last OPTIONS.MaxStallIterations iterations is less than OPTIONS.FunctionTolerance.
x = 1×2
-16.0079 -31.9697
fval = 1.9920
exitflag = 1
Cela semble prometteur : la nouvelle solution a un fval inférieur à la précédente. Mais x est-il vraiment une solution mondiale ? Essayez de minimiser à nouveau avec plus de particules, pour mieux rechercher la région.
options = optimoptions('particleswarm','SwarmSize',100); [x,fval,exitflag] = particleswarm(fun,nvars,lb,ub,options)
Optimization ended: relative change in the objective value over the last OPTIONS.MaxStallIterations iterations is less than OPTIONS.FunctionTolerance.
x = 1×2
-31.9781 -31.9784
fval = 0.9980
exitflag = 1
Cela semble encore plus prometteur. Mais cette réponse est-elle une solution globale et dans quelle mesure est-elle précise ? Réexécutez le solveur avec une fonction hybride. particleswarm appelle la fonction hybride une fois que particleswarm a terminé ses itérations.
options.HybridFcn = @fmincon; [x,fval,exitflag] = particleswarm(fun,nvars,lb,ub,options)
Optimization ended: relative change in the objective value over the last OPTIONS.MaxStallIterations iterations is less than OPTIONS.FunctionTolerance.
x = 1×2
-31.9783 -31.9784
fval = 0.9980
exitflag = 1
particleswarm a trouvé essentiellement la même solution qu'avant. Cela vous donne une certaine confiance que particleswarm signale un minimum local et que le x final est la solution globale.