Pixel Connectivity

Pixel connectivity defines which other pixels each pixel is connected to. A connected group of foreground pixels in a binary image is called an object or a connected component.

This table lists all the standard two- and three-dimensional connectivities supported by the toolbox.

Value	Meaning
Two-Dimensional Connectivities
4	Pixels are connected if their edges touch. Two adjoining pixels are part of the same object if they are both on and are connected along the horizontal or vertical direction.	Current pixel is shown in gray.
8	Pixels are connected if their edges or corners touch. Two adjoining pixels are part of the same object if they are both on and are connected along the horizontal, vertical, or diagonal direction.	Current pixel is shown in gray.
Three-Dimensional Connectivities
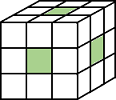
6	Pixels are connected if their faces touch. Two adjoining pixels are part of the same object if they are both on and are connected in: One of these directions: in, out, left, right, up, and down	Current pixel is center of cube.
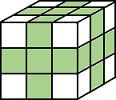
18	Pixels are connected if their faces or edges touch. Two adjoining pixels are part of the same object if they are both on and are connected in: One of these directions: in, out, left, right, up, and down A combination of two directions, such as right-down or in-up	Current pixel is center of cube.
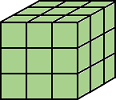
26	Pixels are connected if their faces, edges, or corners touch. Two adjoining pixels are part of the same object if they are both on and are connected in: One of these directions: in, out, left, right, up, and down A combination of two directions, such as right-down or in-up A combination of three directions, such as in-right-up or in-left-down	Current pixel is center of cube.

Choosing a Connectivity

The type of neighborhood you choose affects the number of objects found in an image and the boundaries of those objects. For this reason, the results of many morphology operations can differ depending upon the type of connectivity you specify.

For example, if you specify a 4-connected neighborhood, this binary image contains two objects. If you specify an 8-connected neighborhood, the image contains only one object.

0     0     0     0     0     0
0     1     1     0     0     0
0     1     1     0     0     0
0     0     0     1     1     0
0     0     0     1     1     0

Specifying Custom Connectivities

You can also define custom neighborhoods by specifying a 3-by-3-by-...-by-3 array of 0s and 1s. The 1-valued elements define the connectivity of the neighborhood relative to the center element.

For example, this array defines a North/South connectivity, which you can use to break up an image into independent columns.

CONN = [ 0 1 0; 0 1 0; 0 1 0 ]

CONN =
     0     1     0
     0     1     0
     0     1     0

Note

Connectivity arrays must be symmetric about their center element. Also, you can use a 2-D connectivity array with a 3-D image; the connectivity affects each plane in the 3-D image.