Drape Geoid Heights over Topography
Display geoid data draped over topographic relief. For this example, display the geoid data as a color attribute instead of a 3-D surface.
Load topographic raster data and a geographic cells reference object. Get geoid heights by calling the egm96geoid function and specifying the reference object.
load topo60c
[N,R] = egm96geoid(topo60cR);Create an axesm-based map using a Gall stereographic cylindrical projection (a perspective projection). Use meshm to display variations of the geoid in color, but specify topo60c as the final argument, to give each geoid grid cell the height (z value) of the corresponding topographic grid cell. Low geoid heights are shown as blue, high ones as yellow.
axesm gstereo;
meshm(N,R,size(N),topo60c)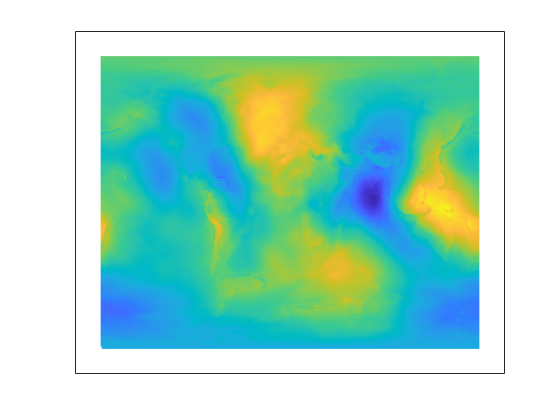
For reference, plot the world coastlines in black, raise their elevation to 1000 meters (high enough to clear the surface in their vicinity), and expand the map to fill the frame.
load coastlines plotm(coastlat,coastlon,'k') zdatam(handlem('allline'),1000) tightmap
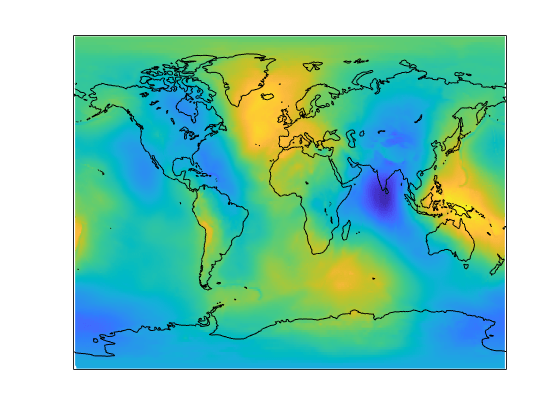
Due to the vertical view and lack of lighting, the topographic relief is not visible, but it is part of the figure's surface data. Bring it out by exaggerating relief greatly, and then setting a view from the south-southeast.
daspectm('m',200); tightmap
view(20,35)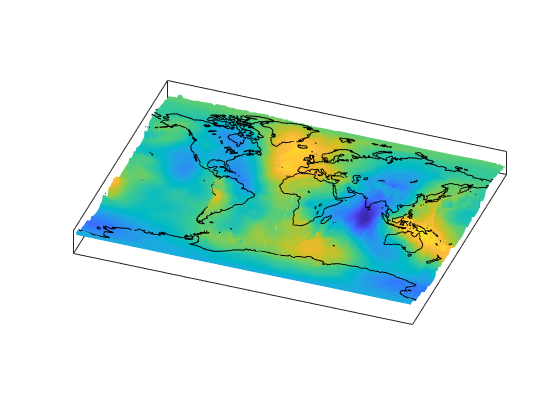
Remove the bounding box, shine a light on the surface (using the default position, offset to the right of the viewpoint), and render again with Gouraud shading.
ax = gca; ax.Box = 'off'; camlight; lighting Gouraud
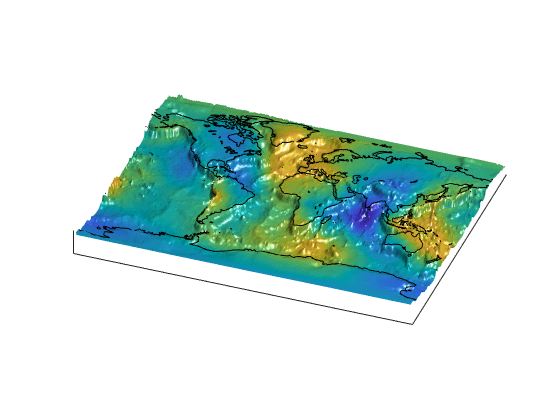
Finally, set the perspective to converge slightly (the default perspective is orthographic). Notice that the geoid mirrors the topography of the major mountain chains such as the Andes, the Himalayas, and the Mid-Atlantic Ridge. You can also see that large areas of high or low geoid heights are not simply a result of topography.
ax.Projection = 'perspective';