Geographic Interpolation of Vectors
When using vector data, remember that, like raster data, coordinates are sampled measurements. This involves unavoidable assumptions concerning what the geographic reality is between specified data points. The normal assumption when plotting vector data requires that points be connected with straight line segments, which essentially indicates a lack of knowledge about conditions between the measured points. For lines that are by nature continuous, such as most rivers and coastlines, such piecewise linear interpolation can be false and misleading, as the following figure depicts.
Interpolating Sparse Vector Data
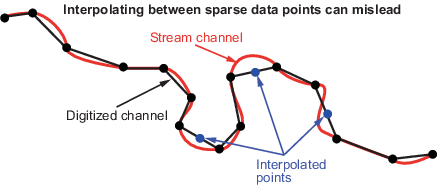
Despite the possibility of misinterpretation, circumstances do exist in which
geographic data interpolation is useful or even necessary. To do this, use the interpm function to interpolate between known data points. One value of
linearly interpolating points is to fill in lines of constant latitude or longitude
(e.g., administrative boundaries) that can curve when projected.
interpm returns both the original data and new linearly
interpolated points. Sometimes, however, you might want only the interpolated values.
The functions intrplat and intrplon work similarly to the MATLAB®
interp1 function, and give you control
over the method used for interpolation. Note that they only interpolate and return one
value at a time. Use intrplat to interpolate a latitude for a given
longitude. Given a monotonic set of longitudes and their matching latitude points, you
can interpolate a new latitude for a longitude you specify, interpolating along linear,
spline, cubic, rhumb line, or great circle paths. The longitudes must increase or
decrease monotonically. If this is not the case, you might be able to use the
intrplon companion function if the latitude values are monotonic.
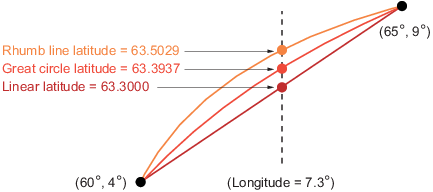
The following diagram illustrates these three types of interpolation. The
intrplat function also can perform spline and cubic spline
interpolations.
Three Types of Interpolation