Build Watts-Strogatz Small World Graph Model
This example shows how to construct and analyze a Watts-Strogatz small-world graph. The Watts-Strogatz model is a random graph that has small-world network properties, such as clustering and short average path length.
Algorithm Description
Creating a Watts-Strogatz graph has two basic steps:
Create a ring lattice with
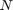 nodes of mean degree
nodes of mean degree 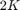 . Each node is connected to its
. Each node is connected to its 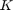 nearest neighbors on either side.
nearest neighbors on either side.For each edge in the graph, rewire the target node with probability
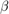 . The rewired edge cannot be a duplicate or self-loop.
. The rewired edge cannot be a duplicate or self-loop.
After the first step the graph is a perfect ring lattice. So when  , no edges are rewired and the model returns a ring lattice. In contrast, when
, no edges are rewired and the model returns a ring lattice. In contrast, when 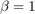 , all of the edges are rewired and the ring lattice is transformed into a random graph.
, all of the edges are rewired and the ring lattice is transformed into a random graph.
The file WattsStrogatz.m implements this graph algorithm for undirected graphs. The input parameters are N, K, and beta according to the algorithm description above.
View the file WattsStrogatz.m.
% Copyright 2015 The MathWorks, Inc. function h = WattsStrogatz(N,K,beta) % H = WattsStrogatz(N,K,beta) returns a Watts-Strogatz model graph with N % nodes, N*K edges, mean node degree 2*K, and rewiring probability beta. % % beta = 0 is a ring lattice, and beta = 1 is a random graph. % Connect each node to its K next and previous neighbors. This constructs % indices for a ring lattice. s = repelem((1:N)',1,K); t = s + repmat(1:K,N,1); t = mod(t-1,N)+1; % Rewire the target node of each edge with probability beta for source=1:N switchEdge = rand(K, 1) < beta; newTargets = rand(N, 1); newTargets(source) = 0; newTargets(s(t==source)) = 0; newTargets(t(source, ~switchEdge)) = 0; [~, ind] = sort(newTargets, 'descend'); t(source, switchEdge) = ind(1:nnz(switchEdge)); end h = graph(s,t); end
Ring Lattice
Construct a ring lattice with 500 nodes using the WattsStrogatz function. When beta is 0, the function returns a ring lattice whose nodes all have degree 2K.
h = WattsStrogatz(500,25,0); plot(h,'NodeColor','k','Layout','circle'); title('Watts-Strogatz Graph with $N = 500$ nodes, $K = 25$, and $\beta = 0$', ... 'Interpreter','latex')

Some Random Edges
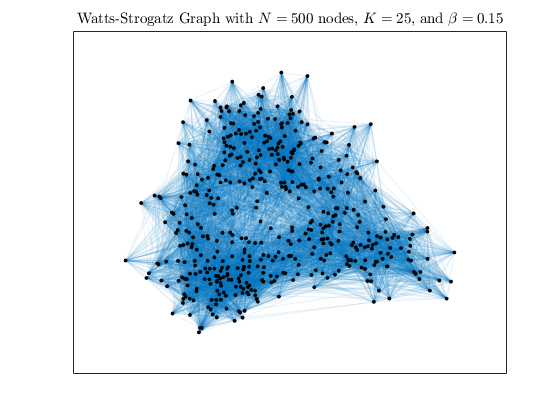
Increase the amount of randomness in the graph by raising beta to 0.15 and 0.50.
h2 = WattsStrogatz(500,25,0.15); plot(h2,'NodeColor','k','EdgeAlpha',0.1); title('Watts-Strogatz Graph with $N = 500$ nodes, $K = 25$, and $\beta = 0.15$', ... 'Interpreter','latex')
h3 = WattsStrogatz(500,25,0.50); plot(h3,'NodeColor','k','EdgeAlpha',0.1); title('Watts-Strogatz Graph with $N = 500$ nodes, $K = 25$, and $\beta = 0.50$', ... 'Interpreter','latex')

Random Graph
Generate a completely random graph by increasing beta to its maximum value of 1.0. This rewires all of the edges.
h4 = WattsStrogatz(500,25,1); plot(h4,'NodeColor','k','EdgeAlpha',0.1); title('Watts-Strogatz Graph with $N = 500$ nodes, $K = 25$, and $\beta = 1$', ... 'Interpreter','latex')

Degree Distribution
The degree distribution of the nodes in the different Watts-Strogatz graphs varies. When beta is 0, the nodes all have the same degree, 2K, so the degree distribution is just a Dirac-delta function centered on 2K,  . However, as
. However, as beta increases, the degree distribution changes.
This plot shows the degree distributions for the nonzero values of beta.
histogram(degree(h2),'BinMethod','integers','FaceAlpha',0.9); hold on histogram(degree(h3),'BinMethod','integers','FaceAlpha',0.9); histogram(degree(h4),'BinMethod','integers','FaceAlpha',0.8); hold off title('Node degree distributions for Watts-Strogatz Model Graphs') xlabel('Degree of node') ylabel('Number of nodes') legend('\beta = 1.0','\beta = 0.50','\beta = 0.15','Location','NorthWest')

Hub Formation
The Watts-Strogatz graph has a high clustering coefficient, so the nodes tend to form cliques, or small groups of closely interconnected nodes. As beta increases towards its maximum value of 1.0, you see an increasingly large number of hub nodes, or nodes of high relative degree. The hubs are a common connection between other nodes and between cliques in the graph. The existence of hubs is what permits the formation of cliques while preserving a short average path length.
Calculate the average path length and number of hub nodes for each value of beta. For the purposes of this example, the hub nodes are nodes with degree greater than or equal to 55. These are all of the nodes whose degree increased 10% or more compared to the original ring lattice.
n = 55; d = [mean(mean(distances(h))), nnz(degree(h)>=n); ... mean(mean(distances(h2))), nnz(degree(h2)>=n); ... mean(mean(distances(h3))), nnz(degree(h3)>=n); mean(mean(distances(h4))), nnz(degree(h4)>=n)]; T = table([0 0.15 0.50 1]', d(:,1), d(:,2),... 'VariableNames',{'Beta','AvgPathLength','NumberOfHubs'})
T =
4×3 table
Beta AvgPathLength NumberOfHubs
____ _____________ ____________
0 5.48 0
0.15 2.0715 20
0.5 1.9101 85
1 1.9008 92
As beta increases, the average path length in the graph quickly falls to its limiting value. This is due to the formation of the highly connected hub nodes, which become more numerous as beta increases.
Plot the  Watts-Strogatz model graph, making the size and color of each node proportional to its degree. This is an effective way to visualize the formation of hubs.
Watts-Strogatz model graph, making the size and color of each node proportional to its degree. This is an effective way to visualize the formation of hubs.
colormap hsv deg = degree(h2); nSizes = 2*sqrt(deg-min(deg)+0.2); nColors = deg; plot(h2,'MarkerSize',nSizes,'NodeCData',nColors,'EdgeAlpha',0.1) title('Watts-Strogatz Graph with $N = 500$ nodes, $K = 25$, and $\beta = 0.15$', ... 'Interpreter','latex') colorbar
