matlab.tall.movingWindow
Apply moving window function to blocks of data
Syntax
Description
[,
where tA,tB,...] = matlab.tall.movingWindow(fcn,window,tX,tY,...)fcn is a function handle that returns multiple outputs, returns
arrays tA,tB,..., each corresponding to one of the output arguments of
fcn. The inputs to fcn are windows of data from the
arguments tX, tY, .... This syntax has these requirements:
fcnmust return the same number of outputs as were requested frommatlab.tall.movingWindow.Each output of
fcnmust be the same type as the first data inputtX.All outputs
tA,tB,...must have the same height.
[___] = matlab.tall.movingWindow(___,
specifies additional options with one or more name-value pair arguments using any of the
previous syntaxes. For example, to adjust the step size between windows, you can specify
Name,Value)'Stride' and a scalar. Or to change the treatment of endpoints where
there are not enough elements to complete a window, you can specify
'EndPoints' and a valid option ('shrink',
'discard', or a numeric padding value).
Examples
Use matlab.tall.movingWindow to calculate the moving median of airline arrival and departure delays.
Create a datastore for the airlinesmall.csv data set and convert it into a tall array. The data contains information about arrival and departure times of US flights. Extract the ArrDelay and DepDelay variables, which are vectors of flight delays, to create a tall array containing the delays as separate columns.
varnames = {'ArrDelay', 'DepDelay'};
ds = tabularTextDatastore('airlinesmall.csv', 'TreatAsMissing', 'NA', ...
'SelectedVariableNames', varnames);
tt = tall(ds);
tX = [tt.ArrDelay tt.DepDelay]tX =
M×2 tall double matrix
8 12
8 1
21 20
13 12
4 -1
59 63
3 -2
11 -1
: :
: :
Use matlab.tall.movingWindow to calculate the moving median of the data in the first dimension. Use a window size of 5,000.
fcn = @(x) median(x,1,'omitnan');
tA = matlab.tall.movingWindow(fcn,5000,tX)tA =
M×N×... tall double array
? ? ? ...
? ? ? ...
? ? ? ...
: : :
: : :
Preview deferred. Learn more.
Gather the unique rows of the result into memory.
tA = gather(unique(tA,'rows'))Evaluating tall expression using the Local MATLAB Session: - Pass 1 of 2: Completed in 0.63 sec - Pass 2 of 2: Completed in 18 sec Evaluation completed in 19 sec
tA = 31×2
-4.0000 -2.0000
-3.5000 -2.0000
-3.0000 -2.0000
-3.0000 -1.5000
-3.0000 -1.0000
-3.0000 -0.5000
-3.0000 0
-2.5000 -1.0000
-2.5000 0
-2.0000 -1.0000
-2.0000 0
-1.5000 0
-1.0000 -1.0000
-1.0000 -0.5000
-1.0000 0
⋮
Use matlab.tall.movingWindow to apply a function with multiple outputs to windows of data.
Create a tall array from an in-memory random matrix.
X = rand(1000,5); tX = tall(X)
tX =
1,000×5 tall double matrix
0.8147 0.6312 0.7449 0.3796 0.4271
0.9058 0.3551 0.8923 0.3191 0.9554
0.1270 0.9970 0.2426 0.9861 0.7242
0.9134 0.2242 0.1296 0.7182 0.5809
0.6324 0.6525 0.2251 0.4132 0.5403
0.0975 0.6050 0.3500 0.0986 0.7054
0.2785 0.3872 0.2871 0.7346 0.0050
0.5469 0.1422 0.9275 0.6373 0.7825
: : : : :
: : : : :
Create a function that finds the sum, mean, median, and mode of each window of data in the first dimension. Each output needs to have the same size in the first dimension, but the other dimensions can have different sizes. For each window of data, the sum calculation produces a scalar, while the other calculations produce 1-by-N vectors.
Save the function in your local workspace.
function [S,mn,mdn,md] = mystats(X) S = sum(X,[2 1]); mn = mean(X,1); mdn = median(X,1); md = mode(X,1); end
Note: This function is included at the end of the example as a local function.
Use matlab.tall.movingWindow to apply the mystats function to the data with a window size of 250. Specify four output arguments to return all of the outputs from mystats. Use the 'EndPoints' name-value pair to discard incomplete windows.
[tS,tmn,tmdn,tmd] = matlab.tall.movingWindow(@mystats, 250, tX, 'EndPoints', 'discard')
tS =
M×N×... tall double array
? ? ? ...
? ? ? ...
? ? ? ...
: : :
: : :
Preview deferred. Learn more.
tmn =
M×N×... tall double array
? ? ? ...
? ? ? ...
? ? ? ...
: : :
: : :
Preview deferred. Learn more.
tmdn =
M×N×... tall double array
? ? ? ...
? ? ? ...
? ? ? ...
: : :
: : :
Preview deferred. Learn more.
tmd =
M×N×... tall double array
? ? ? ...
? ? ? ...
? ? ? ...
: : :
: : :
Preview deferred. Learn more.
function [S,mn,mdn,md] = mystats(X) S = sum(X,[2 1]); mn = mean(X,1); mdn = median(X,1); md = mode(X,1); end
Input Arguments
Window function to apply, specified as a function handle or anonymous function. Each
output of fcn must be the same type as the first input
tX. You can use the 'OutputsLike' option to
return outputs of different data types.
The general functional signature of
fcn
is
[a, b, c, ...] = fcn(x, y, z, ...)
fcn
must satisfy these requirements:
Input Arguments — The inputs
[x, y, z, ...]are blocks of data that fit in memory. The blocks are produced by extracting data from the respective tall array inputs[tX, tY, tZ, ...]. The inputs[x, y, z, ...]satisfy these properties:All of the inputs
[x, y, z, ...]have the same size in the first dimension.The blocks of data in
[x, y, z, ...]come from the same index in the tall dimension, assuming the tall array is nonsingleton in the tall dimension. For example, iftXandtYare nonsingleton in the tall dimension, then the first set of blocks might bex = tX(1:20000,:)andy = tY(1:20000,:).When the first dimension of any of
[tX, tY, tZ, ...]has a size of1, the corresponding block[x, y, z, ...]consists of all the data in that tall array.Applying
fcnmust result in a reduction of the input data to a scalar or a slice of an array of height 1.When the input is a matrix, N-D array, table, or timetable, applying
fcnmust result in a reduction of the input data in each of its columns or variables.
Output Arguments — The outputs
[a, b, c, ...]are blocks that fit in memory, to be sent to the respective outputs[tA, tB, tC, ...]. The outputs[a, b, c, ...]satisfy these properties:All of the outputs
[a, b, c, ...]must have the same size in the first dimension.All of the outputs
[a, b, c, ...]are vertically concatenated with the respective results of previous calls tofcn.All of the outputs
[a, b, c, ...]are sent to the same index in the first dimension in their respective destination output arrays.
Functional Rules —
fcnmust satisfy the functional rule:F([inputs1; inputs2]) == [F(inputs1); F(inputs2)]: Applying the function to the concatenation of the inputs should be the same as applying the function to the inputs separately and then concatenating the results.
For example, this function calculates the mean and standard deviation of the elements in a window and returns two output arrays:
function [mv,sd] = movstats(tX) mv = mean(tX,1,'omitnan'); sd = std(tX,1,'omitnan'); end
[tA,tB] = matlab.tall.movingWindow(@movstats,5,tX)
Example: tA = matlab.tall.movingWindow(@(x) std(x,1,'omitnan'),
tX) specifies an anonymous function to calculate the standard deviation of
each window, ignoring NaNs.
Example: tA = matlab.tall.movingWindow(@mean,3,tX) specifies a
function handle @mean to calculate the mean value of each
three-element window.
Data Types: function_handle
Window size, specified as a positive integer scalar or a two-element row vector [NB NF].
If
windowis a scalar, then:When the window size is odd, each window is centered on the corresponding element in the data.
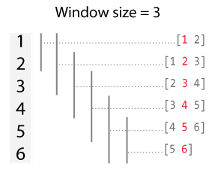
When the window size is even, each window is centered about the current and previous elements.
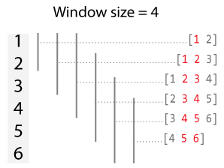
If
windowis a vector[NB NF], then the window includes the previousNBelements, the current element, and the nextNFelements of the inputs.![Illustration of a window size of [2 2] for a vector with six elements. The first window has three elements, the second has four elements, the next two windows have five elements, the second-to-last window has four elements, and the last window has three elements. Each window includes two previous values (when possible), the current value, and the next two values (when possible).](window-size-custom.png)
By default, the window size is automatically truncated at the endpoints when not enough
elements are available to fill the window. When the window is truncated in this manner,
the function operates only on the elements that fill the window. You can change this
behavior with the EndPoints name-value pair.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Input arrays, specified as separate arguments of scalars, vectors, matrices,
multidimensional arrays, tables, or timetables. The input arrays can be tall or
in-memory arrays. The input arrays are used as inputs to the transform function
fcn. Each input array tX,tY,... must have the
same height.
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: tA = matlab.tall.movingWindow(@myFcn, window, tX, 'Stride',
2)
Step size between windows, specified as the comma-separated pair consisting of 'Stride' and a positive integer scalar. After fcn operates on a window of data, the calculation advances by the 'Stride' value before operating on the next window. Increasing the value of 'Stride' from the default value of 1 is the same as reducing the size of the output by picking out every other element, or every third element, and so on.
By default, the value of 'Stride' is 1, so that each window is centered on each element in the input. For example, here is a moving sum calculation with a window size of 3 operating on the vector [1 2 3 4 5 6]':

If the value of 'Stride' is 2, then the calculation changes so that each window is centered on every second element in the input (1, 3, 5). The moving sum now returns three partial sums rather than six:
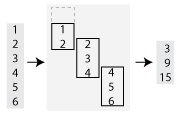
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Method to treat leading and trailing windows, specified as the comma-separated pair consisting of 'EndPoints' and one of the values in the table.
At the beginning and end of a windowed calculation, the window of elements being operated on is incomplete. The 'EndPoints' option specifies how to treat these incomplete windows.
'EndPoints' Value | Description | Example: Moving Sum |
|---|---|---|
| Shrink the window size near the endpoints of the input to include only existing elements. |
|
| Do not output any results where the window does not completely overlap with existing elements. |
|
Numeric or logical padding value | Substitute nonexisting elements with a specified numeric or logical value.
|
|
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical | char | string
Prototype of output arrays, specified as the comma-separated pair consisting of
'OutputsLike' and a cell array containing
prototype arrays. When you specify 'OutputsLike', the
output arrays tA,tB,... returned by
matlab.tall.movingWindow have the same data types and
attributes as the specified prototype arrays {PA,PB,...}.
You must specify 'OutputsLike' whenever the data type of
an output array is different than that of the input array. If you specify
'OutputsLike', then you must specify a prototype
array for each output.
Example: tA = matlab.tall.movingWindow(..., tX, 'OutputsLike', {int8(1)});, where
tX is a double-precision tall array, returns tA as
int8 instead of double.
Data Types: cell
Output Arguments
Output arrays, returned as scalars, vectors, matrices, or multidimensional arrays.
If any input to matlab.tall.movingWindow is tall, then all output
arguments are also tall. Otherwise, all output arguments are in-memory arrays.
The size and data type of the output arrays depend on the specified window function
fcn.The output arrays
tA,tB,...all have the same height, which depends on the value of'Stride'and'EndPoints'. By default the output arrays are the same size as the input arrays.In general, the outputs
tA,tB,...must all have the same data type as the first inputtX. However, you can specify'OutputsLike'to return different data types. In cases where the input arraystX, tY, ...are empty, or when'EndPoints'is'discard'and there are not enough elements to fill a full-sized window,matlab.tall.movingWindowreturns empty outputs. The sizes of the empty outputs are based on the size of the input arraytX, or on the sizes of the prototype arrays provided to'OutputsLike', if specified.
Tips
Use
matlab.tall.movingWindowfor simple sliding-window calculations.matlab.tall.blockMovingWindowis an advanced API designed to provide more flexibility to perform sliding-window calculations on tall arrays. As such, it is more complicated to use since the functions must accurately process blocks of data that contain many complete windows. However, with properly vectorized calculations, you can reduce the necessary number of function calls and improve performance.
Version History
Introduced in R2019a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Sélectionner un site web
Choisissez un site web pour accéder au contenu traduit dans votre langue (lorsqu'il est disponible) et voir les événements et les offres locales. D’après votre position, nous vous recommandons de sélectionner la région suivante : .
Vous pouvez également sélectionner un site web dans la liste suivante :
Comment optimiser les performances du site
Pour optimiser les performances du site, sélectionnez la région Chine (en chinois ou en anglais). Les sites de MathWorks pour les autres pays ne sont pas optimisés pour les visites provenant de votre région.
Amériques
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)

