Adaptive Cruise Control System Using Model Predictive Control
This example shows how to use the Adaptive Cruise Control System block in Simulink® and demonstrates the control objectives and constraints of this block.
Adaptive Cruise Control System
A vehicle (ego car) equipped with adaptive cruise control (ACC) has a sensor, such as radar, that measures the distance to the preceding vehicle in the same lane (lead car),  . The sensor also measures the relative velocity of the lead car,
. The sensor also measures the relative velocity of the lead car,  . The ACC system operates in the following two modes:
. The ACC system operates in the following two modes:
Speed control: The ego car travels at a driver-set speed.
Spacing control: The ego car maintains a safe distance from the lead car.
The ACC system decides which mode to use based on real-time radar measurements. For example, if the lead car is too close, the ACC system switches from speed control to spacing control. Similarly, if the lead car is further away, the ACC system switches from spacing control to speed control. In other words, the ACC system makes the ego car travel at a driver-set speed as long as it maintains a safe distance.
The following rules are used to determine the ACC system operating mode:
If
 , then speed control mode is active. The control goal is to track the driver-set velocity,
, then speed control mode is active. The control goal is to track the driver-set velocity,  .
.
If
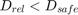 , then spacing control mode is active. The control goal is to maintain the safe distance,
, then spacing control mode is active. The control goal is to maintain the safe distance, 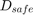 .
.

Simulink Model for Lead Car and Ego Car
The dynamics for lead car and ego car are modeled in Simulink. Open the Simulink model.
mdl = 'mpcACCsystem';
open_system(mdl)

To approximate a realistic driving environment, the acceleration of the lead car varies according to a sine wave during the simulation. The Adaptive Cruise Control System block outputs an acceleration control signal for the ego car.
Define the sample time, Ts, and simulation duration, T, in seconds.
Ts = 0.1; T = 80;
For both the ego vehicle and the lead vehicle, the dynamics between acceleration and velocity are modeled as:

which approximates the dynamics of the throttle body and vehicle inertia.
Specify the linear model for ego car.
G_ego = tf(1,[0.5,1,0]);
Specify the initial position and velocity for the two vehicles.
x0_lead = 50; % initial position for lead car (m) v0_lead = 25; % initial velocity for lead car (m/s) x0_ego = 10; % initial position for ego car (m) v0_ego = 20; % initial velocity for ego car (m/s)
Configuration of Adaptive Cruise Control System Block
The ACC system is modeled using the Adaptive Cruise Control System Block in Simulink. The inputs to the ACC system block are:
Driver-set velocity

Time gap
Velocity of the ego car

Relative distance to the lead car
 (from radar)
(from radar)Relative velocity to the lead car
 (from radar)
(from radar)
The output for the ACC system is the acceleration of the ego car.
The safe distance between the lead car and the ego car is a function of the ego car velocity,  :
:

where  is the standstill default spacing and
is the standstill default spacing and 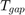 is the time gap between the vehicles. Specify values for
is the time gap between the vehicles. Specify values for  , in meters, and
, in meters, and 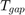 , in seconds.
, in seconds.
t_gap = 1.4; D_default = 10;
Specify the driver-set velocity in m/s.
v_set = 30;
Considering the physical limitations of the vehicle dynamics, the acceleration is constrained to the range [-3,2] (m/s^2).
amin_ego = -3; amax_ego = 2;
For this example, the default parameters of the Adaptive Cruise Control System block match the simulation parameters. If your simulation parameters differ from the default values, then update the block parameters accordingly.
Simulation Analysis
Run the simulation.
sim(mdl)
-->Converting model to discrete time. -->Assuming output disturbance added to measured output #2 is integrated white noise. Assuming no disturbance added to measured output #1. -->"Model.Noise" is empty. Assuming white noise on each measured output.
Plot the simulation result.
mpcACCplot(logsout,D_default,t_gap,v_set)

In the first 3 seconds, to reach the driver-set velocity, the ego car accelerates at full throttle.
From 3 to 13 seconds, the lead car accelerates slowly. As a result, to maintain a safe distance to the lead car, the ego car accelerates with a slower rate.
From 13 to 25 seconds, the ego car maintains the driver-set velocity, as shown in the Velocity plot. However, as the lead car reduces speed, the spacing error starts approaching 0 after 20 seconds.
From 25 to 45 seconds, the lead car slows down and then accelerates again. The ego car maintains a safe distance from the lead car by adjusting its speed, as shown in the Distance plots.
From 45 to 56 seconds, the spacing error is above 0. Therefore, the ego car achieves the driver-set velocity again.
From 56 to 76 seconds, the deceleration/acceleration sequence from the 25 to 45 second interval is repeated.
Throughout the simulation, the controller ensures that the actual distance between the two vehicles is greater than the set safe distance. When the actual distance is sufficiently large, then the controller ensures that the ego vehicle follows the driver-set velocity.