step

System object: phased.MFSKWaveform
Namespace: phased

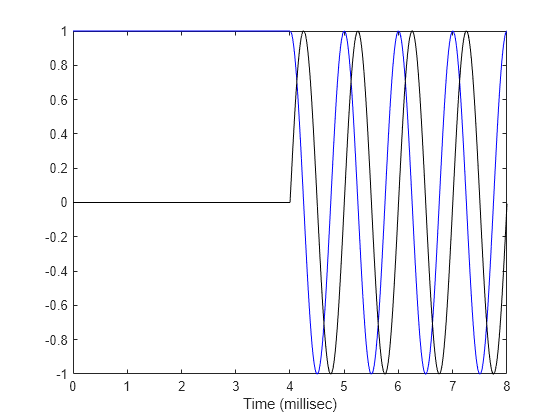
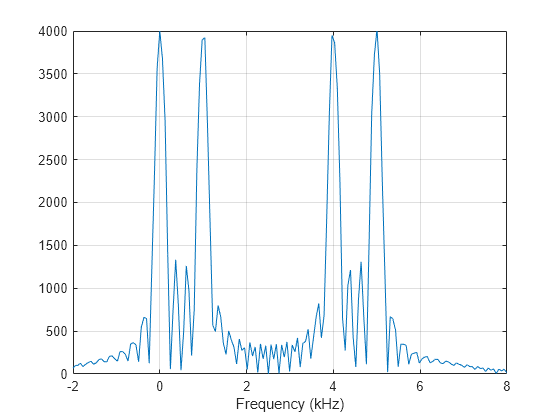
Samples of continuous MFSK waveform

Syntax

Y = step(sMFSK)


Description

Note

Starting in R2016b, instead of using the step method to perform the operation defined by the System object™, you can call the object with arguments, as if it were a function. For example, y = step(obj,x) and y = obj(x) perform equivalent operations. When the only argument to the step method is the System object itself, replace y = step(obj) by y = obj().

Y = step(sMFSK) returns samples of the MFSK waveform in a N-by-1 complex valued column vector, Y.

Note

The object performs an initialization the first time the object is executed. This initialization locks nontunable properties and input specifications, such as dimensions, complexity, and data type of the input data. If you change a nontunable property or an input specification, the System object issues an error. To change nontunable properties or inputs, you must first call the release method to unlock the object.

Input Arguments

sMFSK — MFSK waveform

System object

MFSK waveform, specified as a phased.MFSKWaveform System object.

Example: sMFSK= phased.MFSKWaveform;

Output Arguments

Y — Output samples

N-by-1 complex valued vector

Output samples of MFSK waveform, returned as an N-by-1 complex valued vector. When the step method reaches the end of the waveform, the output samples wrap around from the start of the waveform, yielding a periodic waveform.

Examples

Construct MFSK Step Output

Construct an MFSK waveform with a sample rate of 1 MHz and a sweep bandwidth of 0.1 MHz. Assume 52 steps, with a step time of 4 milliseconds. Set the frequency offset to 1 kHz. There are 4000 samples per step.

fs = 1e6;
fsweep = 1e5;
tstep = 40e-4;
numsteps = 52;
foffset = 1000;
noutputsteps = 4;
sMFSK = phased.MFSKWaveform('SampleRate',fs,...
    'SweepBandwidth',fsweep,...
    'StepTime',tstep,...
    'StepsPerSweep',numsteps,...
    'FrequencyOffset',foffset,...
    'OutputFormat','Steps',...
    'NumSteps',noutputsteps);

Call the step method to retrieve the samples for the four steps.

z = step(sMFSK);

Plot the real and imaginary parts of the first two steps.

samplesperstep = fs*tstep;
disp(samplesperstep)

        4000

idx = [1:2*samplesperstep]';
time = idx/fs*1000;
plot(time,real(z(idx)),'b',time,imag(z(idx)),'k');
xlabel('Time (millisec)')

Compute the FFT of all the data.

n = size(z,1);
nfft = 2^ceil(log2(n));
Y = fftshift(fft(z,nfft));

Plot the magnitudes of the spectrum.

fmax = fs/2;
ft = [-nfft/2:nfft/2-1]*fmax/(nfft/2);
figure(2);
hp = plot(ft/1000,abs(Y));
axis([-2,8,-1,4000]);
xlabel('Frequency (kHz)')
grid

The plot shows two pairs of peaks. The first pair lies at 0 Hz and 1000 Hz. The second pair lies at 4000 Hz and 5000 Hz. The frequency offset is 1000 Hz.

Compute the frequency increase to the second pair off peaks.

fdelta = fsweep/(numsteps/2-1);
disp(fdelta)

        4000

The increase agrees with the location of the second pair of peaks in the FFT spectrum.

MFSK Samples per Sweep

Construct an MFSK waveform with a sample rate of 1 MHz and a sweep bandwidth of 0.1 MHz. Assume 52 steps with a step time of 400 microseconds. Set the frequency offset to 1 kHz. Find the number of samples returned when the OutputFormat property is set to return the samples for one sweep.

fs = 1e6;
fsweep = 1e5;
tstep = 40e-4;
numsteps = 52;
foffset = 1000;
noutputsweeps = 1;
sMFSK = phased.MFSKWaveform('SampleRate',fs,...
    'SweepBandwidth',fsweep,...
    'StepTime',tstep,...
    'StepsPerSweep',numsteps,...
    'FrequencyOffset',foffset,...
    'OutputFormat','Sweeps',...
    'NumSweeps',noutputsweeps);

Call the step method to retrieve the samples for the four steps.

z = step(sMFSK);

Count the number of samples in a sweep.

samplespersweep = fs*tstep*numsteps;
disp(samplespersweep)

      208000

Verify that this value agrees with the number of samples returned by the step method.

disp(size(z))

      208000           1

Version History

Introduced in R2015a