Sinc Antenna as Approximation for Array Response Pattern
This example shows how a sinc antenna element can approximate the radiation pattern of an array.
Create a 5-by-2 rectangular array of isotropic elements designed to work at an operating frequency of 3 GHz. Specify an element spacing equal to half the wavelength.
fc = 3e9; lambda = freq2wavelen(fc); array = phased.URA('ElementSpacing',lambda/2,'Size',[5 2]);
Compute the radiation pattern of the array. Specify a range of azimuth angles from –90° to 90° and zero elevation. Plot the unnormalized azimuth pattern in polar coordinates.
az = -90:0.5:90;
recopts = {'CoordinateSystem','rectangular','Type','powerdb'};
polopts = {'CoordinateSystem','polar','Type','powerdb'};
arrayPatternAz = pattern(array,fc,az,0,recopts{:});
pattern(array,fc,az,0,polopts{:})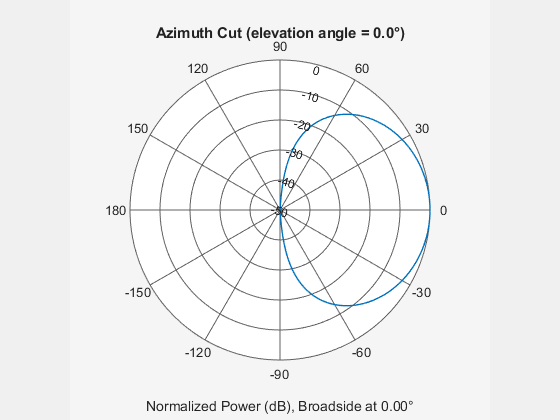
Normalize the pattern so that its maximum value is 0 dB. Compute the azimuth beamwidth.
arrayPatternAzNorm = arrayPatternAz - max(arrayPatternAz); arrayAzBw = beamwidth(array,fc);
Compute the radiation for a range of elevation angles from –90° to 90° and zero azimuth. Normalize the pattern and compute the beamwidth. Plot the unnormalized elevation pattern in polar coordinates.
el = -90:0.5:90;
arrayPatternEl = pattern(array,fc,0,el,recopts{:});
arrayPatternElNorm = arrayPatternEl - max(arrayPatternEl);
arrayElBw = beamwidth(array,fc,'Cut','Elevation');
pattern(array,fc,0,el,polopts{:})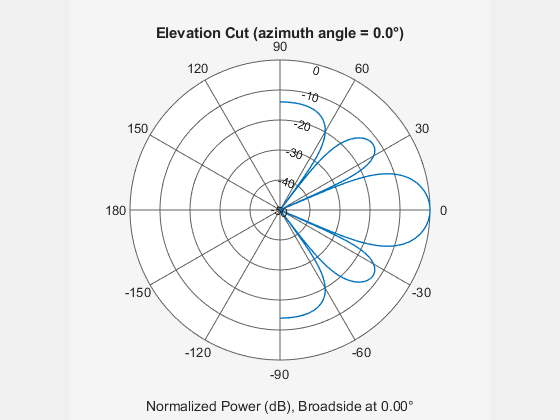
Create a sinc antenna element with the same beamwidth as the array. Compute the azimuth and elevation patterns. The patterns are normalized by construction.
se = phased.SincAntennaElement('Beamwidth',[arrayAzBw arrayElBw]);
sePatternAz = pattern(se,fc,az,0,recopts{:});
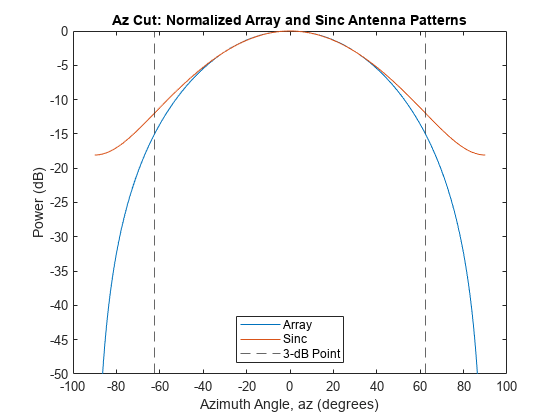
sePatternEl = pattern(se,fc,0,el,recopts{:});Find the smallest positive azimuth angle at which the patterns differ by about 3 dB. Plot the azimuth patterns in rectangular coordinates. Overlay the 3-dB points. The sinc azimuth pattern matches the array azimuth pattern well out to about 60 degrees.
idxAz = find((abs(arrayPatternAzNorm - sePatternAz) >= 3) & (az' >= 0),1); az3dB = az(idxAz); figure plot(az,arrayPatternAzNorm,az,sePatternAz) xline([-az3dB az3dB],'--') title("Az Cut: Normalized Array and Sinc Antenna Patterns") xlabel("Azimuth Angle, az (degrees)") ylabel("Power (dB)") legend("Array","Sinc","3-dB Point",Location="south") ylim([-50 0])
Repeat the process for the elevation patterns. The sinc pattern is a good approximation out to about 20 degrees.
idxEl = find((abs(arrayPatternElNorm - sePatternEl) >= 3) & (el' >= 0),1); el3dB = el(idxEl); plot(el,arrayPatternElNorm,az,sePatternEl) xline([-el3dB el3dB],'--') title("El Cut: Normalized Array and Sinc Antenna Patterns") xlabel("Elevation Angle, el (degrees)") ylabel("Power (dB)") legend("Array","Sinc","3-dB Point") ylim([-50 0])
