convertVibration
Compute baseline-corrected and filtered acceleration, velocity, and displacement signals from vibration measurements using a single sensor output from either an accelerometer, velocity sensor, or displacement sensor
Since R2024a
Syntax
Description
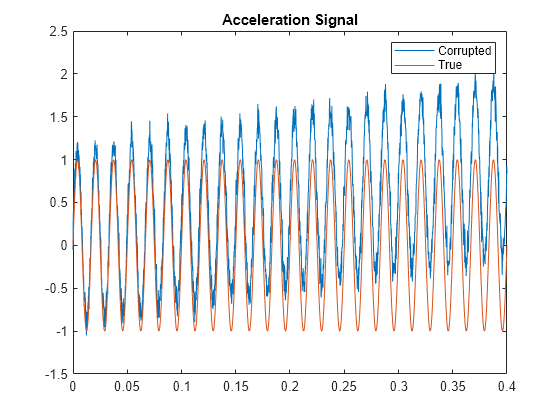
The convertVibration function converts accelerometer signals
into baseline-corrected and filtered velocity and displacement signals. This function is
especially useful when you plan to perform machine vibration monitoring using ISO 10816 and
20816
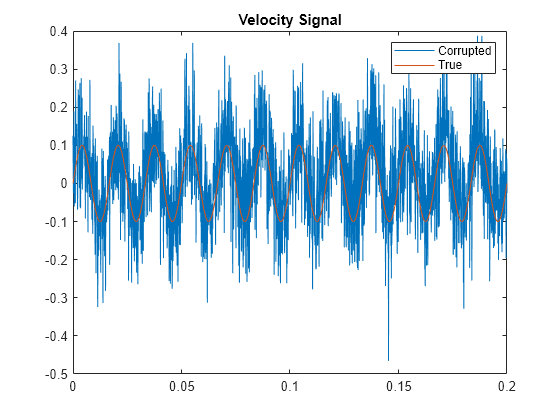
vibration standards. You can also use convertVibration to convert
displacement or velocity measurements into the three signal forms.
The ISO standards are provided for RMS velocity measurements (in mm/s) and displacement
measurements (in μm), but not for accelerometer measurements (in g or
mm/s2). convertVibration uses a combination
of high-pass filtering, integration, and baseline correction to accurately convert
accelerometer measurements into both velocity and displacement signals. The function uses a
similar algorithm to convert position signals to acceleration, but with differentiation
instead of integration. Converting velocity signals to acceleration and position uses a
combination of differentiation and integration.
The units in the convertVibration output signals are consistent with
the units of the input signals and the integration or differentiation functions that the
function performs.
Integration (such as acceleration to velocity): Input-signal unit is multiplied by seconds, so, for example, m/s2 becomes m/s.
Differentiation: (such as displacement to velocity): Input-signal unit is divided by seconds, so, for example, m becomes m/s.
If the input is in units of g, you must multiply the output by 9.81 to convert the results to m/s (velocity) or m (displacement).
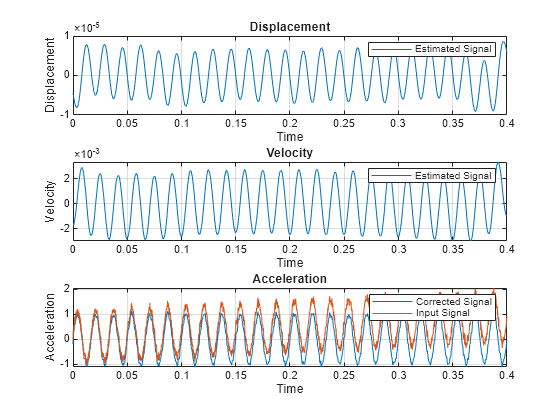
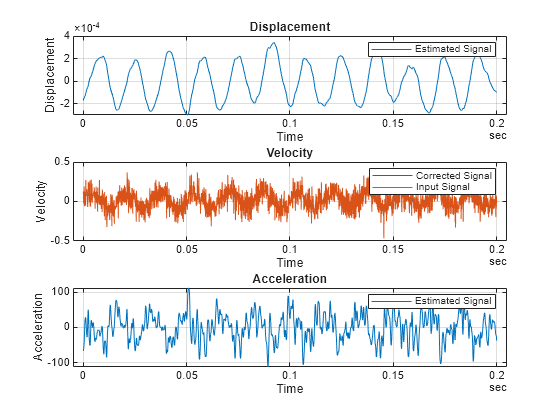
Return Converted Signals
[___] = convertVibration(___,
allows you to specify additional parameters using one or more name-value arguments. For
example, if your data in Name=Value)T represents a velocity signal rather than
an acceleration signal, use the name-value argument
Type="velocity".
[___,
also returns the Options] = convertVibration(___)Options structure containing various parameter values
that the software used to perform the conversion, such as sampling frequency
Fs and lowpass filter cutoff frequency
Fmax.
You can use this syntax with any of the previous input and output argument combinations.
Plot Converted Signals
convertVibration(___) plots the converted
signals.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
Algorithms
The convertVibration algorithm is based on the numerical integrator
design described in [1]. The
integrator contains three stages, each stage of which includes some combination and sequence
of offset or baseline calibration, highpass filtering, and integration. The result is a stable
velocity signal and displacement signal. The following block diagram, adapted from [1],
illustrates the general algorithm flow for an accelerometer input.
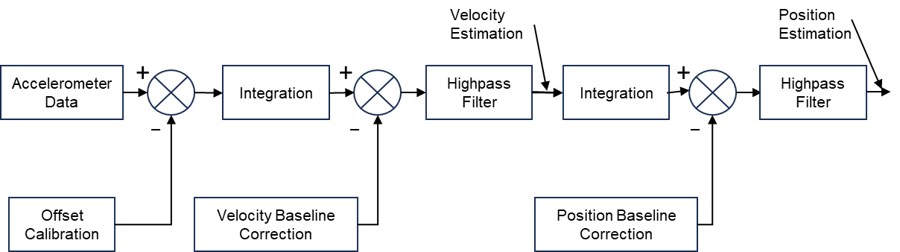
A similar algorithm converts position data to the three corrected outputs, but uses
differentiation instead of integration. For converting velocity data,
convertVibration uses a combination of integration and
differentiation.
References
[1] S. Thenozhi, W. Yu and R. Garrido, "A novel numerical integrator for structural health monitoring." 2012 5th International Symposium on Resilient Control Systems, Salt Lake City, UT, USA, 2012, pp. 92-97, doi: 10.1109/ISRCS.2012.6309300.
Version History
Introduced in R2024a