Train DDPG Agent to Control Sliding Robot
This example shows how to train a deep deterministic policy gradient (DDPG) agent to generate trajectories for a robot sliding without friction over a 2-D plane, modeled in Simulink®. For more information on DDPG agents, see Deep Deterministic Policy Gradient (DDPG) Agent.
Fix Random Number Stream for Reproducibility
The example code might involve computation of random numbers at various stages. Fixing the random number stream at the beginning of various sections in the example code preserves the random number sequence in the section every time you run it, and increases the likelihood of reproducing the results. For more information, see Results Reproducibility.
Fix the random number stream with seed 0 and random number algorithm Mersenne Twister. For more information on controlling the seed used for random number generation, see rng.
previousRngState = rng(0,"twister");The output previousRngState is a structure that contains information about the previous state of the stream. You will restore the state at the end of the example.
Sliding Robot Model
The reinforcement learning environment for this example is a sliding robot with its initial condition randomized around a ring having a radius of 15 m. The orientation of the robot is also randomized. The robot has two thrusters mounted on the side of the body that are used to propel and steer the robot. The training goal is to drive the robot from its initial condition to the origin facing east.
Open the model.
mdl = "rlSlidingRobotEnv";
open_system(mdl)Set the initial model state variables.
theta0 = 0; x0 = -15; y0 = 0;
Define the sample time Ts and the simulation duration Tf.
Ts = 0.4; Tf = 30;
In this model:
The goal orientation is
0rad (robot facing east).The thrust from each actuator is bounded from -1 to 1 N
The observations from the environment are the position, orientation (sine and cosine of orientation), velocity, and angular velocity of the robot.
The reward provided at every time step is
where:
is the position of the robot along the x-axis.
is the position of the robot along the y-axis.
is the orientation of the robot.
is the control effort from the left thruster.
is the control effort from the right thruster.
is the reward when the robot is close to the goal.
is the penalty when the robot drives beyond 20 m in either the x or y direction. The simulation is terminated when .
is a QR penalty that penalizes distance from the goal and control effort.
Create Integrated Model
To train an agent for the SlidingRobotEnv model, use the createIntegratedEnv function to automatically generate a Simulink model containing an RL Agent block that is ready for training.
integratedMdl = "IntegratedSlidingRobot"; [~,agentBlk,obsInfo,actInfo] = ... createIntegratedEnv(mdl,integratedMdl);
Actions and Observations
Before creating the environment object, specify names for the observation and action specifications, and bound the thrust actions between -1 and 1.
The observation vector for this environment is . Assign a name to the environment observation channel.
obsInfo.Name = "observations";The action vector for this environment is . Assign a name, as well as upper and lower limits, to the environment action channel.
actInfo.Name = "thrusts";
actInfo.LowerLimit = -ones(prod(actInfo.Dimension),1);
actInfo.UpperLimit = ones(prod(actInfo.Dimension),1);Note that prod(obsInfo.Dimension) and prod(actInfo.Dimension) return the number of dimensions of the observation and action spaces, respectively, regardless of whether they are arranged as row vectors, column vectors, or matrices.
Create Environment Object
Create an environment object using the integrated Simulink model.
env = rlSimulinkEnv( ... integratedMdl, ... agentBlk, ... obsInfo, ... actInfo);
Reset Function
Create a custom reset function that randomizes the initial position of the robot along a ring of radius 15 m and the initial orientation. For details on the reset function, see slidingRobotResetFcn.
env.ResetFcn = @(in) slidingRobotResetFcn(in);
Create DDPG agent
DDPG agents use a parametrized Q-value function approximator to estimate the value of the policy. A Q-value function critic takes the current observation and an action as inputs and returns a single scalar as output (the estimated discounted cumulative long-term reward given the action from the state corresponding to the current observation, and following the policy thereafter).
When you create the agent, the initial parameters of the critic network are initialized with random values. Fix the random number stream so that the agent is always initialized with the same parameter values.
rng(0,"twister");To model the parametrized Q-value function within the critic, use a neural network with two input layers (one for the observation channel, as specified by obsInfo, and the other for the action channel, as specified by actInfo) and one output layer (which returns the scalar value).
Define each network path as an array of layer objects. Assign names to the input and output layers of each path. These names allow you to connect the paths and then later explicitly associate the network input and output layers with the appropriate environment channel.
% Specify the number of outputs for the hidden layers. hiddenLayerSize = 128; % Define observation path layers observationPath = [ featureInputLayer(prod(obsInfo.Dimension),Name="obsInLyr") concatenationLayer(1,2,Name="cat") fullyConnectedLayer(hiddenLayerSize) reluLayer fullyConnectedLayer(hiddenLayerSize) reluLayer fullyConnectedLayer(hiddenLayerSize) reluLayer fullyConnectedLayer(1,Name="fc4") ]; % Define action path layers actionPath = featureInputLayer( ... prod(actInfo.Dimension), ... Name="actInLyr");
Assemble a dlnetwork object.
criticNetwork = dlnetwork(); criticNetwork = addLayers(criticNetwork,observationPath); criticNetwork = addLayers(criticNetwork,actionPath);
Connect actionPath to observationPath.
criticNetwork = connectLayers(criticNetwork,"actInLyr","cat/in2");
Initialize network and display the number of parameters.
criticNetwork = initialize(criticNetwork); summary(criticNetwork)
Initialized: true
Number of learnables: 34.4k
Inputs:
1 'obsInLyr' 7 features
2 'actInLyr' 2 features
Create the critic using criticNetwork, the environment specifications, and the names of the network input layers to be connected to the observation and action channels. For more information see rlQValueFunction.
critic = rlQValueFunction(criticNetwork,obsInfo,actInfo,... ObservationInputNames="obsInLyr",ActionInputNames="actInLyr");
DDPG agents use a parametrized deterministic policy over continuous action spaces, which is learned by a continuous deterministic actor. This actor takes the current observation as input and returns as output an action that is a deterministic function of the observation.
To model the parametrized policy within the actor, use a neural network with one input layer (which receives the content of the environment observation channel, as specified by obsInfo) and one output layer (which returns the action to the environment action channel, as specified by actInfo).
Define the network as an array of layer objects.
actorNetwork = [
featureInputLayer(prod(obsInfo.Dimension))
fullyConnectedLayer(hiddenLayerSize)
reluLayer
fullyConnectedLayer(hiddenLayerSize)
reluLayer
fullyConnectedLayer(hiddenLayerSize)
reluLayer
fullyConnectedLayer(prod(actInfo.Dimension))
tanhLayer
];Convert the array of layer object to a dlnetwork object, initialize the network, and display the number of parameters.
actorNetwork = dlnetwork(actorNetwork); actorNetwork = initialize(actorNetwork); summary(actorNetwork)
Initialized: true
Number of learnables: 34.3k
Inputs:
1 'input' 7 features
Define the actor using actorNetwork, and the specifications for the action and observation channels. For more information, see rlContinuousDeterministicActor.
actor = rlContinuousDeterministicActor(actorNetwork,obsInfo,actInfo);
Specify options for the critic and the actor using rlOptimizerOptions.
criticOptions = rlOptimizerOptions( ... LearnRate=1e-03, ... GradientThreshold=5); actorOptions = rlOptimizerOptions( ... LearnRate=1e-03, ... GradientThreshold=5);
Specify the DDPG agent options using rlDDPGAgentOptions, include the training options for the actor and critic.
agentOptions = rlDDPGAgentOptions(... SampleTime=Ts,... ActorOptimizerOptions=actorOptions,... CriticOptimizerOptions=criticOptions,... ExperienceBufferLength=1e6 ,... TargetSmoothFactor=1e-3,... MiniBatchSize=512,... MaxMiniBatchPerEpoch=50); % Gaussian noise agentOptions.NoiseOptions.MeanAttractionConstant = 1/Ts; agentOptions.NoiseOptions.StandardDeviation = 1e-1; agentOptions.NoiseOptions.StandardDeviationMin = 1e-2; agentOptions.NoiseOptions.StandardDeviationDecayRate = 1e-6;
Then, create the agent using the actor, the critic and the agent options. For more information, see rlDDPGAgent.
agent = rlDDPGAgent(actor,critic,agentOptions);
Alternatively, you can create the agent first, and then access its option object and modify the options using dot notation.
Train Agent
To train the agent, first specify the training options. For this example, use the following options:
Run each training for a maximum of
10000episodes, with each episode lasting at mostceil(Tf/Ts)time steps.Display the training progress in the Reinforcement Learning Training Monitor (set the
Plotsoption) and disable the command line display (set theVerboseoption tofalse).Evaluate the trained greedy policy every 50 training episodes by averaging the cumulative reward over 5 simulations.
Stop training the agent when the average cumulative reward obtained during the evaluation episodes equals of exceeds
425. At this point, the agent can drive the sliding robot to the goal position.
For more information on training options, see rlTrainingOptions.
maxepisodes = 10000; maxsteps = ceil(Tf/Ts); trainingOptions = rlTrainingOptions(... MaxEpisodes=maxepisodes,... MaxStepsPerEpisode=maxsteps,... StopOnError="on",... Verbose=false,... Plots="training-progress",... StopTrainingCriteria="EvaluationStatistic",... StopTrainingValue=425,... ScoreAveragingWindowLength=10); % agent evaluator evl = rlEvaluator(EvaluationFrequency=50,NumEpisodes=5);
Fix the random stream for reproducibility.
rng(0,"twister");Train the agent using the train function. Training is a computationally intensive process that takes several hours to complete. To save time while running this example, load a pretrained agent by setting doTraining to false. To train the agent yourself, set doTraining to true.
doTraining =false; if doTraining % Train the agent. trainingStats = train(agent,env,trainingOptions,Evaluator=evl); else % Load the pretrained agent for the example. load("SlidingRobotDDPG.mat","agent") end
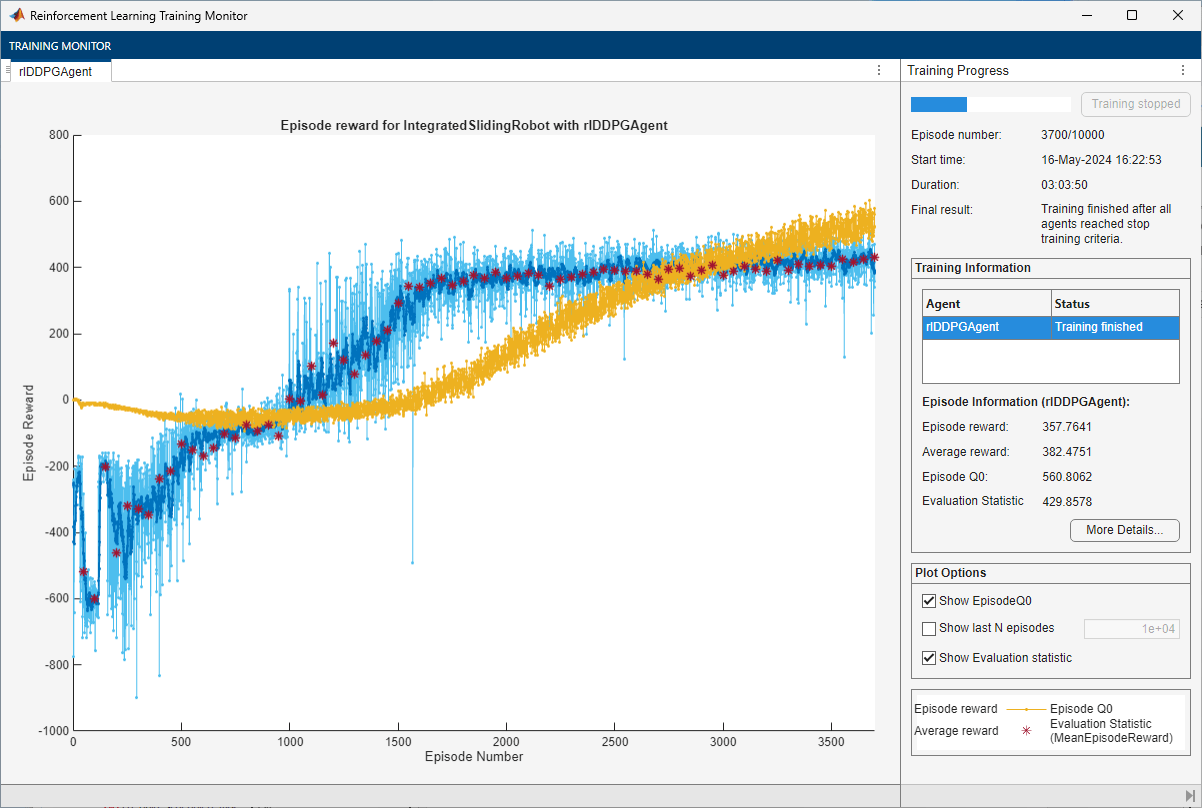
Simulate DDPG Agent
Fix the random stream for reproducibility.
rng(0,"twister");To validate the performance of the trained agent, simulate the agent within the environment. For more information on agent simulation, see rlSimulationOptions and sim.
simOptions = rlSimulationOptions(MaxSteps=maxsteps); experience = sim(env,agent,simOptions);
Restore the random number stream using the information stored in previousRngState.
rng(previousRngState);
See Also
Functions
Objects
rlDDPGAgent|rlDDPGAgentOptions|rlQValueFunction|rlContinuousDeterministicActor|rlTrainingOptions|rlSimulationOptions|rlOptimizerOptions
Blocks
Topics
- Train DDPG Agent to Swing Up and Balance Cart-Pole System
- Train DDPG Agent to Swing Up and Balance Pendulum with Image Observation
- Train PPO Agent for a Lander Vehicle
- Trajectory Optimization and Control of Flying Robot Using Nonlinear MPC (Model Predictive Control Toolbox)
- Create Custom Simulink Environments
- Deep Deterministic Policy Gradient (DDPG) Agent
- Train Reinforcement Learning Agents