Train DQN Agent Using Hindsight Experience Replay
This example shows how to train a deep Q-learning network (DQN) agent using hindsight experience replay in a discrete navigation problem.
Discrete Navigation Environment
The reinforcement learning environment for this example is a simple discrete 2-D navigation problem. The training goal is to make a robot reach the goal state.
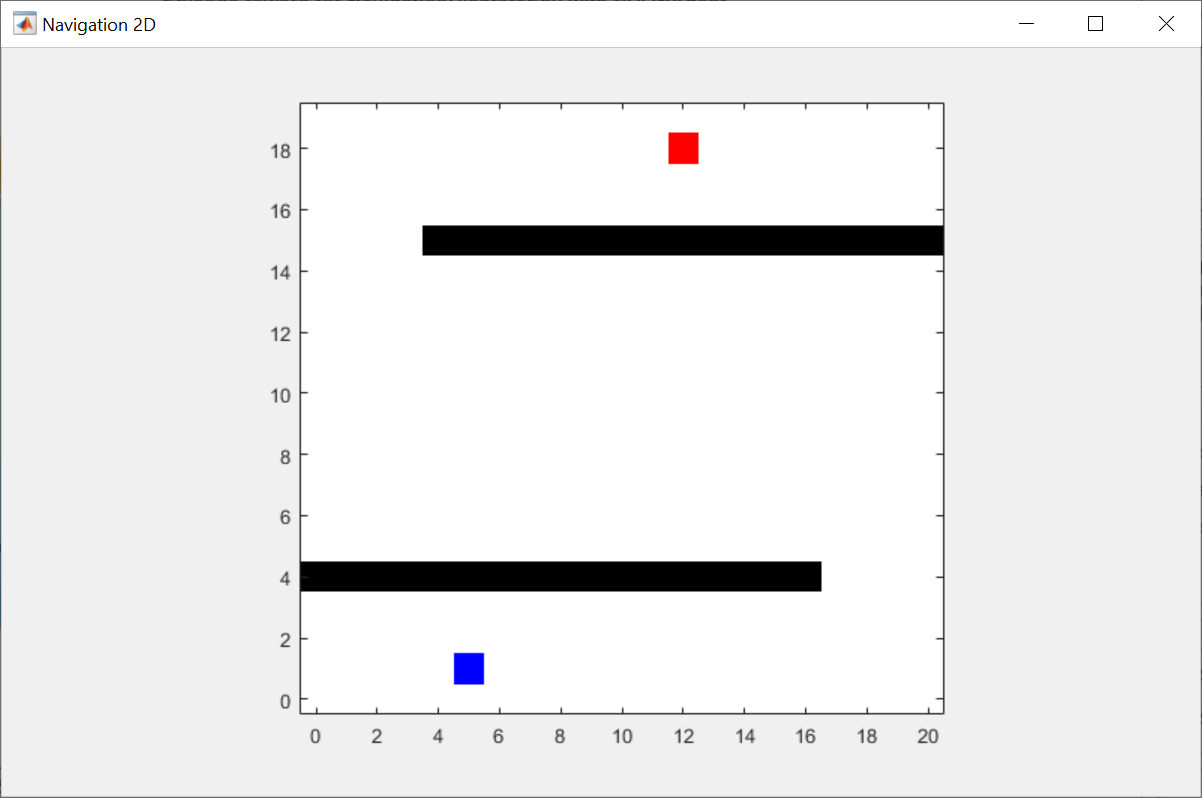
The environment is a 20-by-20 grid containing a robot (blue), a goal (red), and obstacles (black).
The navigation problem in this example is a goal-conditioned task for which the observation from the environment contains both the goal (navigation target) and the goal measurement (robot position). The observation column vector contains the robot position and the navigation target .
The initial position of the robot and the goal are sampled as follows:
where is a discrete uniform distribution between and .
The discrete actions for this environment are defined as follows:
If the action leads to the obstacle location or the map's boundary, the robot doesn't move.
The reward signal is defined as follows:
where is the next observation, and
Terminal condition is defined as follows:
Fix Random Number Stream for Reproducibility
The example code might involve computation of random numbers at various stages. Fixing the random number stream at the beginning of various sections in the example code preserves the random number sequence in the section every time you run it, and increases the likelihood of reproducing the results. For more information, see Results Reproducibility. Fix the random number stream with seed 0 and random number algorithm Mersenne twister. For more information on controlling the seed used for random number generation, see rng.
previousRngState = rng(1,"twister");The output previousRngState is a structure that contains information about the previous state of the stream. You will restore the state at the end of the example.
Create Environment Interface
Create a discrete navigation environment. NavigationDiscreteEnv.m is located in this example folder.
env = NavigationDiscreteEnv;
Create DQN Agent
For a given observation and action, a DQN agent estimates the value of the policy (the cumulative discounted long-term reward) using a parameterized Q-value function critic.
Create a default DQN agent from the environment specifications. For more information on DQN agents, see rlDQNAgent.
obsInfo = getObservationInfo(env); actInfo = getActionInfo(env); agent = rlDQNAgent(obsInfo,actInfo);
Specify the DQN agent options, including training options for the critic. Alternatively, you can use rlDQNAgentOptions object.
agent.AgentOptions.EpsilonGreedyExploration.Epsilon = 1.0; agent.AgentOptions.EpsilonGreedyExploration.EpsilonMin = 0.1; agent.AgentOptions.EpsilonGreedyExploration.EpsilonDecay = 1e-5; agent.AgentOptions.MiniBatchSize = 128; agent.AgentOptions.CriticOptimizerOptions.LearnRate = 5e-4; agent.AgentOptions.CriticOptimizerOptions.GradientThreshold = 1;
Construct Hindsight Replay Memory
The DQN agent is unable to efficiently learn a good policy with a default replay memory because of the sparse rewards. You can improve the sample efficiency by using a hindsight replay memory for a goal-conditioned task with sparse rewards. The hindsight experience replay augments the acquired experiences by replacing the goal with the goal measurement so that agent can use the data that reaches the replaced goal. Thus, the agent can be trained with meaningful rewards even if the agent does not reach the goal.
To use a hindsight replay memory, set ExperienceBuffer of the agent to rlHindsightReplayMemory. You need to specify the following.
A reward function: The reward function,
myNavigationGoalRewardFcn, computes the true reward given observation, action, and next observation.An is-done function: The is-done function,
myNavigationGoalIsDoneFcn, computes the true is-done signal given observation, action, and the next observation.Goal condition information:
goalConditionInfospecifies the channel and indices of goal measurements and goals. In this example, there is only one observation channel; the first and second observation elements correspond to the goal measurements (the robot position), and the third and fourth observation elements correspond to the goal position.Experience buffer length (optional): This examples uses 1e5.
myNavigationGoalRewardFcn.m and myNavigationGoalIsDoneFcn.m are located in this example folder. For more information, type help rlHindsightReplayMemory.
To use a standard replay memory, set useHER to false.
useHER = true; if useHER rewardFcn = @myNavigationGoalRewardFcn; isDoneFcn = @myNavigationGoalIsDoneFcn; % observation is [robot_x, robot_y, goal_x, goal_y]' % goal measurement: channel --- 1, indices --- 1,2 % goal: channel --- 1, indices --- 3,4 goalConditionInfo = {{1,[1,2], 1, [3,4]}}; bufferLength = 1e5; agent.ExperienceBuffer = rlHindsightReplayMemory(obsInfo,actInfo,... rewardFcn,isDoneFcn,goalConditionInfo,bufferLength); else agent.AgentOptions.ExperienceBufferLength = 1e5; end
Train Agent
To train the agent, first specify the training options. For this example, use the following options:
Run one training session containing 3000 episodes, with each episode lasting at most 120 time steps.
Display the training progress in the Reinforcement Learning Training Monitor dialog box (set the
Plotsoption) and disable the command line display (set theVerboseoption tofalse).Set the Plots options to "training-progress".
Stop training when the agent receives an evaluation statistic (the mean value of evaluation episode rewards in this example) greater than 1.0.
For more information on training options, see rlTrainingOptions.
maxEpisodes = 3000; maxStepsPerEpisode = 120; trainOpts = rlTrainingOptions(... MaxEpisodes=maxEpisodes, ... MaxStepsPerEpisode=maxStepsPerEpisode, ... Verbose=false, ... ScoreAveragingWindowLength=100,... Plots="training-progress",... StopTrainingCriteria="EvaluationStatistic",... StopTrainingValue=1.0);
Use an rlEvaluator object to evaluate the agent periodically during training and to use the evaluation statistic for the stop training criteria. For this example, use the following options:
Run 10 evaluation episodes at every 50 training episodes.
Use random seeds from 101 to 110 so that the same initial conditions can be used. For example, the first evaluation episode uses 101, and the 10th evaluation episode uses 110.
The evaluator uses the mean of the evaluation episode rewards as the default for "EvaluationStatisticType".
evaluator = rlEvaluator( ... EvaluationFrequency=50, ... NumEpisodes=10, ... RandomSeeds=101:110);
You can visualize the environment by using the plot function during training or simulation.
plot(env)

Train the agent using the train function. Training this agent is a computationally intensive process. To save time while running this example, load a pretrained agent by setting doTraining to false. To train the agent yourself, set doTraining to true.
doTraining = false; if doTraining % Train the agent. trainingStats = train(agent,env,trainOpts, Evaluator=evaluator); else % Load the pretrained agent for the example. load("DiscreteNavigationDQNAgent.mat","agent") end
The following figure shows a snapshot of training progress.

Simulate DQN Agent
Since the reset function randomizes the reference values, fix the random generator seed to ensure simulation reproducibility.
rng(2)
To validate the performance of the trained agent, simulate it within the navigation environment. For more information on agent simulation, see rlSimulationOptions and sim.
simOptions = rlSimulationOptions(... NumSimulations=1,... MaxSteps=maxStepsPerEpisode); simResults = sim(env,agent,simOptions);

The trained agent successfully reached the goal.
Restore the random number stream using the information stored in previousRngState.
rng(previousRngState);
Reference
Andrychowicz, Marcin, Filip Wolski, Alex Ray, Jonas Schneider, Rachel Fong, Peter Welinder, Bob McGrew, Josh Tobin, Pieter Abbeel, and Wojciech Zaremba. "Hindsight experience replay." Advances in neural information processing systems 30 (2017).
See Also
Functions
Objects
rlHindsightReplayMemory|rlHindsightPrioritizedReplayMemory|rlTrainingOptions|rlSimulationOptions|rlDQNAgent|rlDQNAgentOptions