Introduction to Equal and Unequal Split Wilkinson Power Splitter
This example shows you how to design, analyze, and compare an equal and unequal Wilkinson splitter.
A Wilkinson power splitter is a device that is matched at all ports. This splitter is lossless when excited at the input port and the output ports are isolated. You can also make this splitter to perform arbitrary power division which is the unequal Wilkinson splitter.
Equal Split Wilkinson with Rectangular Shape
Use the wilkinsonSplitter object to create an equal split Wilkinson splitter. For this case the reference impedance is 50 Ohms. The split lines have an impedance of 70.7 ohms and the Isolation Resistor between the two output ports is 100 Ohms. The split lines have the same width and have a length equal to a quarter wavelength. The port lines have an impedance of 50 Ohms.
splitter = wilkinsonSplitter; figure; show(splitter);

The Shape property on the wilkinson splitter is used to create the geometry with rectangular bends or circular rings. The default shape property is Rectangular which creates split lines with rectangular bends.
Use the sparameters function to compute the S-parameters and plot it using the rfplot function.
spar = sparameters(splitter,linspace(1e9,5e9,31)); figure; rfplot(spar);

The result shows an S11 value of -25 dB at 1.8 GHz. The S21 and S31 are overlapping each other with a value of -3.1 dB. This overlap indicates an equal power division to the output ports. The Isolation is also higher than -25 dB at 1.8 GHz. The output ports are matched over the entire simulated frequency range and S22 and S33 value is higher than -25 dB at 1.8 GHz.
Use the design method to design Wilkinson splitter at 2 GHz and visualize it.
splitter = design(splitter,2e9); figure; show(splitter);

Compute and plot the S-parameters of the 2 GHz splitter.
spar = sparameters(splitter,linspace(1e9,3e9,31)); figure; rfplot(spar);

The result shows an S11 value of -30 dB close to the design frequency of 2 GHz. The S21 and S31 overlaps each other indicating an equal power division to output ports. The isolation is also higher than -30 dB at the design frequency. The output ports are matched over the entire simulated frequency range and the S22 and S33 value is higher than -20 dB at the design frequency.
Use the current function to plot the current distribution on the surface of the Wilkinson power splitter.
figure; current(splitter,2e9);

Equal Split wilkinson with Circular Shape
Use the Shape property of the Wilkinson to change the splitter shape to Circular.
splitter.Shape = 'Circular';
figure;
show(splitter);
For a reference impedance of 50 Ohms, the input PortLine and two output PortLines have an impedances of 50 ohms. Both the SplitLines have the same width and the same impedance of 70.7 ohms. The resistance between the two lines is represented by the 100 ohm load. Since the Shape property is Circular, the SplitLines are created using an annular ring.
Compute and plot the S-parameters of the splitter.
spar = sparameters(splitter,linspace(1e9,5e9,31)); figure; rfplot(spar);

The result shows an S11 value of -25 dB at 2 GHz. The S21 and S31 overlap each other with a value of -3.1 dB at the resonant frequency. This indicates an equal power division to output ports. The Isolation is also better than -25 dB at 1.8 GHz. The output ports are matched over the entire simulated frequency range and the S22 and S33 value is higher than -25 dB at 1.8 GHz.
Design the Wilkinson splitter at 4 GHz.
splitter = design(splitter,4e9); figure; show(splitter);

Compute and plot the S-parameters.
spar = sparameters(splitter,linspace(3e9,5e9,31)); figure; rfplot(spar);

The result shows an S11 value of -20 dB close to the design frequency of 4 GHz. The S21 and S31 overlap on each other indicating an equal power division to output ports. The Isolation is also better than -20 dB at the design frequency. The output ports are matched over the entire simulated frequency range and the S22 and S33 value is -20 dB at the design frequency.
Compute and plot the current distribution on the surface of the splitter.
figure; current(splitter,4e9);

Design and Analysis of the Unequal Split wilkinson Power Splitter
The unequal Wilkinson splitter divides the power unequally to the output ports. Because of the unequal division, the impedance of both the arms of the power splitter and width of the split lines are different. Two more microstrip lines are used to match the split lines to the reference impedance. Both the SplitLine and the MatchLine are quarter wavelength long.
Use the wilkinsonSplitterUnequal object to create a Wilkinson splitter and use the show function to visualize it.
splitter = wilkinsonSplitterUnequal; figure; show(splitter);

Design the Wilkinson splitter at 2 GHz and specify the power ratio between the ports as 2.
splitter = design(splitter,2e9,'PowerRatio',2);
figure;
show(splitter);
Compute and plot the S-parameters.
spar = sparameters(splitter,linspace(1e9,3e9,31)); figure; rfplot(spar);
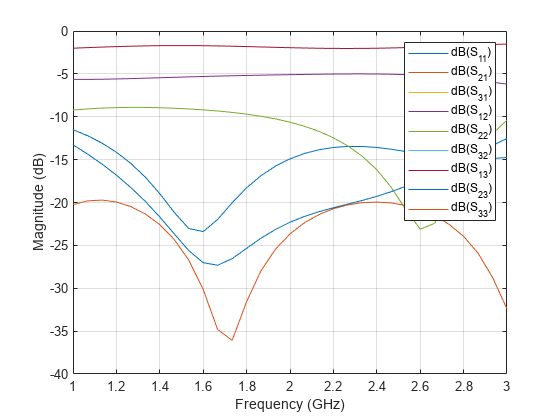
The result shows an S11 value higher than -30 dB close to the design frequency of 2 GHz. The S21 value is close to the expected value of -1.76 dB and S31 value is close to the expected value of -4.77 dB. These values indicate an unequal division to output ports. The Isolation is also higher than -30 dB at the design frequency. The output ports are matched over the entire simulated frequency range and S22 and S33 value is better than -20 dB at the design frequency.
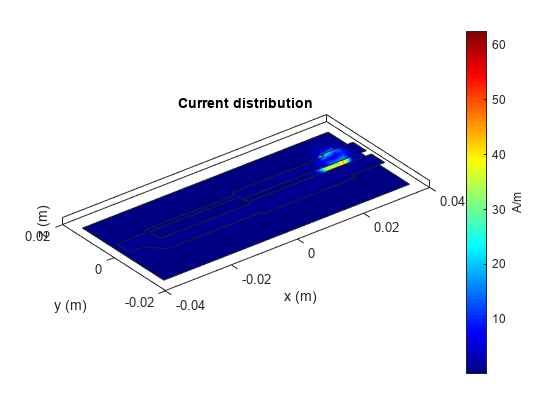
Compute and plot the current distribution on the surface of the Wilkinson power splitter.
figure; current(splitter,2e9);
Change the PowerRatio to 4 in the design method.
splitter = design(splitter,2.5e9,'PowerRatio',4);
figure;
show(splitter);
Computer and plot the S-parameters.
spar = sparameters(splitter,linspace(1e9,4e9,31)); figure; rfplot(spar);

The result shows an S11 value higher than -30 dB close to the design frequency of 2.5 GHz. The S21 value is close to the expected value of -0.97 dB and S31 value is close to the expected value of -6.99 dB. These values indicate an unequal division to output ports with the power ratio of 4. The Isolation is also higher than -20 dB at the design frequency. The output ports are matched over the entire simulated frequency range and S22 and S33 value is better than -15 dB at the design frequency.
Compute and plot current distribution on the surface of the Wilkinson power splitter.
figure; current(splitter,2.5e9);
