Building and Manipulating Uncertain Models
This example shows how to use Robust Control Toolbox™ software to build uncertain state-space models and analyze the robustness of feedback control systems with uncertain elements.
We will show how to specify uncertain physical parameters and create uncertain state-space models from these parameters. You will see how to evaluate the effects of random and worst-case parameter variations using the functions usample and robstab.
Two-Cart and Spring System
In this example, we use the following system consisting of two frictionless carts connected by a spring k.
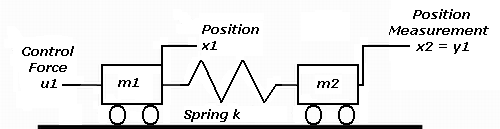
Figure 1: Two-cart and spring system.
The control input is the force u1 applied to the left cart. The output to be controlled is the position y1 of the right cart. The feedback control is of the following form:
In addition, we use a triple-lead compensator:
We create this compensator using this code:
s = zpk('s'); % The Laplace 's' variable C = 100*ss((s+1)/(.001*s+1))^3;
Block Diagram Model
The two-cart and spring system is modeled by the block diagram shown below.

Figure 2: Block diagram of two-cart and spring model.
Uncertain Real Parameters
The problem of controlling the carts is complicated by the fact that the values of the spring constant k and cart masses m1,m2 are known with only 20% accuracy: , , and . To capture this variability, we will create three uncertain real parameters using the ureal function:
k = ureal('k',1,'percent',20); m1 = ureal('m1',1,'percent',20); m2 = ureal('m2',1,'percent',20);
Uncertain Cart Models
We can represent the carts models as follows:
Given the uncertain parameters m1 and m2, we will construct uncertain state-space models (USS) for G1 and G2 as follows:
G1 = 1/s^2/m1; G2 = 1/s^2/m2;
Uncertain Model of a Closed-Loop System
First we'll construct a plant model P corresponding to the block diagram shown above (P maps u1 to y1):
% Spring-less inner block F(s)
F = [0;G1]*[1 -1]+[1;-1]*[0,G2]Uncertain continuous-time state-space model with 2 outputs, 2 inputs, 4 states. The model uncertainty consists of the following blocks: m1: Uncertain real, nominal = 1, variability = [-20,20]%, 1 occurrences m2: Uncertain real, nominal = 1, variability = [-20,20]%, 1 occurrences Model Properties Type "F.NominalValue" to see the nominal value and "F.Uncertainty" to interact with the uncertain elements.
Connect with the spring k.
P = lft(F,k)
Uncertain continuous-time state-space model with 1 outputs, 1 inputs, 4 states. The model uncertainty consists of the following blocks: k: Uncertain real, nominal = 1, variability = [-20,20]%, 1 occurrences m1: Uncertain real, nominal = 1, variability = [-20,20]%, 1 occurrences m2: Uncertain real, nominal = 1, variability = [-20,20]%, 1 occurrences Model Properties Type "P.NominalValue" to see the nominal value and "P.Uncertainty" to interact with the uncertain elements.
The feedback control u1 = C*(r-y1) operates on the plant P as shown below:

Figure 3: Uncertain model of a closed-loop system.
We'll use the feedback function to compute the closed-loop transfer from r to y1.
% Uncertain open-loop model is
L = P*CUncertain continuous-time state-space model with 1 outputs, 1 inputs, 7 states. The model uncertainty consists of the following blocks: k: Uncertain real, nominal = 1, variability = [-20,20]%, 1 occurrences m1: Uncertain real, nominal = 1, variability = [-20,20]%, 1 occurrences m2: Uncertain real, nominal = 1, variability = [-20,20]%, 1 occurrences Model Properties Type "L.NominalValue" to see the nominal value and "L.Uncertainty" to interact with the uncertain elements.
Uncertain closed-loop transfer from r to y1 is
T = feedback(L,1)
Uncertain continuous-time state-space model with 1 outputs, 1 inputs, 7 states. The model uncertainty consists of the following blocks: k: Uncertain real, nominal = 1, variability = [-20,20]%, 1 occurrences m1: Uncertain real, nominal = 1, variability = [-20,20]%, 1 occurrences m2: Uncertain real, nominal = 1, variability = [-20,20]%, 1 occurrences Model Properties Type "T.NominalValue" to see the nominal value and "T.Uncertainty" to interact with the uncertain elements.
Note that since G1 and G2 are uncertain, both P and T are uncertain state-space models.
Extracting the Nominal Plant
The nominal transfer function of the plant is
Pnom = zpk(P.nominal)
Pnom =
1
-------------
s^2 (s^2 + 2)
Continuous-time zero/pole/gain model.
Model Properties
Nominal Closed-Loop Stability
Next, we evaluate the nominal closed-loop transfer function Tnom, and then check that all the poles of the nominal system have negative real parts:
Tnom = zpk(T.nominal); maxrealpole = max(real(pole(Tnom)))
maxrealpole = -0.8232
Robust Stability Margin
Will the feedback loop remain stable for all possible values of k,m1,m2 in the specified uncertainty range? We can use the robstab function to answer this question rigorously.
% Show report and compute sensitivity opt = robOptions('Display','on','Sensitivity','on'); [StabilityMargin,wcu] = robstab(T,opt);
Computing peak... Percent completed: 100/100
System is robustly stable for the modeled uncertainty.
-- It can tolerate up to 288% of the modeled uncertainty.
-- There is a destabilizing perturbation amounting to 289% of the modeled uncertainty.
-- This perturbation causes an instability at the frequency 575 rad/seconds.
-- Sensitivity with respect to each uncertain element is:
12% for k. Increasing k by 25% decreases the margin by 3%.
47% for m1. Increasing m1 by 25% decreases the margin by 11.8%.
47% for m2. Increasing m2 by 25% decreases the margin by 11.8%.
The report indicates that the closed loop can tolerate up to three times as much variability in k,m1,m2 before going unstable. It also provides useful information about the sensitivity of stability to each parameter. The variable wcu contains the smallest destabilizing parameter variations (relative to the nominal values).
wcu
wcu = struct with fields:
k: 1.5773
m1: 0.4227
m2: 0.4227
Worst-Case Performance Analysis
Note that the peak gain across frequency of the closed-loop transfer T is indicative of the level of overshoot in the closed-loop step response. The closer this gain is to 1, the smaller the overshoot. We use wcgain to compute the worst-case gain PeakGain of T over the specified uncertainty range.
[PeakGain,wcu] = wcgain(T); PeakGain
PeakGain = struct with fields:
LowerBound: 1.0474
UpperBound: 1.0731
CriticalFrequency: 7.3245
Substitute the worst-case parameter variation wcu into T to compute the worst-case closed-loop transfer Twc.
Twc = usubs(T,wcu); % Worst-case closed-loop transfer TFinally, pick from random samples of the uncertain parameters and compare the corresponding closed-loop transfers with the worst-case transfer Twc.
Trand = usample(T,4); % 4 random samples of uncertain model T clf subplot(211), bodemag(Trand,'b',Twc,'r',{10 1000}); % plot Bode response subplot(212), step(Trand,'b',Twc,'r',0.2); % plot step response

Figure 4: Bode diagram and step response.
In this analysis, we see that the compensator C performs robustly for the specified uncertainty on k,m1,m2.
See Also
ureal | uss | robstab | wcgain | usubs