fibonacci

Fibonacci numbers

collapse all in page

Syntax

fibonacci(n)

Description

example

fibonacci(n) returns the n^th Fibonacci Number.

Examples

Find Fibonacci Numbers

Find the sixth Fibonacci number by using fibonacci.

fibonacci(6)

ans =
     8

Find the first 10 Fibonacci numbers.

n = 1:10;
fibonacci(n)

ans =
     1     1     2     3     5     8    13    21    34    55

Fibonacci Sequence Approximates Golden Ratio

The ratio of successive Fibonacci numbers converges to the golden ratio $1.61803 . . .$ . Show this convergence by plotting this ratio against the golden ratio for the first 10 Fibonacci numbers.

n = 2:10;
ratio = fibonacci(n)./fibonacci(n-1);

plot(n,ratio,'--o')
hold on

line(xlim,[1.618 1.618])
hold off

Figure contains an axes object. The axes object contains 2 objects of type line.

Symbolically Represent Fibonacci Numbers

Use Fibonacci numbers in symbolic calculations by representing them with symbolic input. fibonacci returns the input.

Represent the n^th Fibonacci number.

syms n
fibonacci(n)

ans =
fibonacci(n)

Find Large Fibonacci Numbers

Find large Fibonacci numbers by specifying the input symbolically using sym. Symbolic input returns exact symbolic output instead of double output. Convert symbolic numbers to double by using the double function.

Find the 300^th Fibonacci number.

num = sym(300);
fib300 = fibonacci(num)

fib300 =
222232244629420445529739893461909967206666939096499764990979600

Convert fib300 to double. The result is a floating-point approximation.

double(fib300)

ans =
   2.2223e+62

For more information on symbolic and double arithmetic, see Choose Numeric or Symbolic Arithmetic.

Golden Spiral Using Fibonacci Numbers

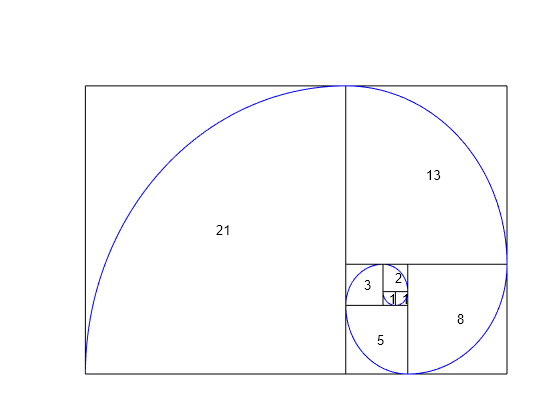
The Fibonacci numbers are commonly visualized by plotting the Fibonacci spiral. The Fibonacci spiral approximates the golden spiral.

Approximate the golden spiral for the first 8 Fibonacci numbers. Define the four cases for the right, top, left, and bottom squares in the plot by using a switch statement. Form the spiral by defining the equations of arcs through the squares in eqnArc. Draw the squares and arcs by using rectangle and fimplicit respectively.

x = 0;
y = 1;
syms v u

axis off
hold on

for n = 1:8

    a = fibonacci(n);

    % Define squares and arcs
    switch mod(n,4)
        case 0
            y = y - fibonacci(n-2);
            x = x - a;
            eqnArc = (u-(x+a))^2 + (v-y)^2 == a^2;
        case 1
            y = y - a;
            eqnArc = (u-(x+a))^2 + (v-(y+a))^2 == a^2;
        case 2
            x = x + fibonacci(n-1);
            eqnArc = (u-x)^2 + (v-(y+a))^2 == a^2;
        case 3
            x = x - fibonacci(n-2);
            y = y + fibonacci(n-1);
            eqnArc = (u-x)^2 + (v-y)^2 == a^2;
    end

    % Draw square
    pos = [x y a a];
    rectangle('Position', pos)

    % Add Fibonacci number
    xText = (x+x+a)/2;
    yText = (y+y+a)/2;
    text(xText, yText, num2str(a))

    % Draw arc
    interval = [x x+a y y+a];
    fimplicit(eqnArc, interval, 'b')

end

Input Arguments

collapse all

`n` — Input
number | vector | matrix | multidimensional array | symbolic number | symbolic variable | symbolic vector | symbolic matrix | symbolic multidimensional array | symbolic function | symbolic expression

Input, specified as a number, vector, matrix or multidimensional array, or a symbolic number, variable, vector, matrix, multidimensional array, function, or expression.

More About

collapse all

Fibonacci Number

The Fibonacci numbers are the sequence 0, 1, 1, 2, 3, 5, 8, 13, 21….

Given that the first two numbers are 0 and 1, the n^th Fibonacci number is

F_n = F_n–1 + F_n–2.

Applying this formula repeatedly generates the Fibonacci numbers.

Version History

Introduced in R2017a