2-D Convolution
Compute 2-D discrete convolution of two input matrices
Libraries:
Computer Vision Toolbox /
Filtering
Description
The 2-D Convolution block computes the two-dimensional convolution of two input matrices. Assume that matrix A has dimensions (Ma, Na) and matrix B has dimensions (Mb, Nb). When the block calculates the full output size, the equation for the 2-D discrete convolution is:
where and .
Examples
Blur Image Using Gaussian Kernel
Perform 2-D convolution to blur an image using the Gaussian kernel.
Ports
Input
Input matrix, specified as either a matrix of intensity values or a matrix that represents one plane of an RGB video stream.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | fixed point
Input matrix, specified as either a matrix of intensity values or a matrix that represents one plane of an RGB video stream.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | fixed point
Output
Convolution of the input matrices, returned as a matrix.
Dependencies
The dimensions of the output are dictated by the Output size parameter.
If the data type of the input is floating point, the output of the block is also floating point.
If
all(size(I1)<size(I2)), the block returns an error.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | fixed point
Parameters
Main Tab
Dimensions of the output.
The table describes the block output, given the following input dimensions:
I1 — (Ma, Na)
I2 — (Mb, Nb)
| Output size | Output | Output Dimension |
|---|---|---|
Full | Full two-dimensional convolution | (Ma+Mb-1, Na+Nb-1). |
Same as input port I1 | Central part of the convolution with the same dimensions as the input at port I1 | |
Valid | Only the parts of the convolution that are computed without the zero-padded edges of any input. | (Ma-Mb+1, Na-Nb+1) |
Normalize output by dividing the output by
sqrt(sum(dot(I1p,I1p))*sum(dot(I2,I2))), where
I1p is the portion of the I1 matrix
that aligns with the I2 matrix.
Note
When you select the Normalized output check box, the block input cannot be fixed point.
Data Types Tab
For details on the fixed-point block parameters, see Specify Fixed-Point Attributes for Blocks (DSP System Toolbox).
Block Characteristics
Data Types |
|
Multidimensional Signals |
|
Variable-Size Signals |
|
Algorithms
In convolution, the value of an output element is computed as a weighted sum of neighboring elements.
For example, suppose the first input matrix represents an image and is defined as:
I1 = [17 24 1 8 15
23 5 7 14 16
4 6 13 20 22
10 12 19 21 3
11 18 25 2 9]
The second input matrix also represents an image and is defined as:
I2 = [8 1 6
3 5 7
4 9 2]
The following figure shows how to compute the (1,1) output element by using these steps:
Rotate the second input matrix, I2, 180 degrees around its center element.
Slide the center element of I2 so that it lies on top of the (0,0) element of I1.
Multiply each element of the rotated I2 matrix by the element of I1 underneath.
Sum the individual products from step 3.
The (1,1) output element is .
Computing the (1,1) Output of Convolution

The normalized convolution of the (1,1) output element is
220/sqrt(sum(dot(I1p,I1p))*sum(dot(I2,I2))) = 0.3459, where
I1p = [0 0 0; 0 17 24; 0 23 5].
The equations below describe how the block computes the convolution depending on how you set the Output size parameter. For the cases below, the inputs are set as:
I1 — dimensions (4,3)
I2 — dimensions (2,2)
When Output size is set to
Full, the block uses the following equations:
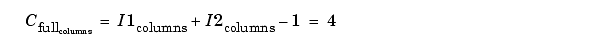
The resulting matrix is:

When Output size is set to
Same as input port I1, the output is the central part of with the same dimensions as the input at port I1, (4,3). However, since a 4-by-3 matrix cannot be extracted from the exact center of , the block leaves more rows and columns on the top and left side of the matrix and outputs:
When the Output size is set to
Valid, the block uses the following equations to determine the number of rows and columns of the output matrix: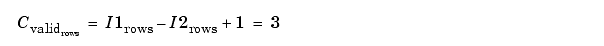
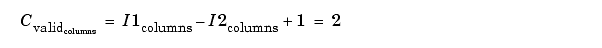
In this case, it is always possible to extract the exact center of . Therefore, the block outputs:

Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.
When you select the Normalized output check box, the block input cannot be fixed point.
Version History
Introduced before R2006a
See Also
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Sélectionner un site web
Choisissez un site web pour accéder au contenu traduit dans votre langue (lorsqu'il est disponible) et voir les événements et les offres locales. D’après votre position, nous vous recommandons de sélectionner la région suivante : .
Vous pouvez également sélectionner un site web dans la liste suivante :
Comment optimiser les performances du site
Pour optimiser les performances du site, sélectionnez la région Chine (en chinois ou en anglais). Les sites de MathWorks pour les autres pays ne sont pas optimisés pour les visites provenant de votre région.
Amériques
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)

