La traduction de cette page n'est pas à jour. Cliquez ici pour voir la dernière version en anglais.

Analyse par ondelettes discrète

Le logiciel Wavelet Toolbox™ vous permet d'analyser des signaux, des images et des données 3D à l'aide de l'analyse par ondelettes discrète orthogonales et biorthogonales à échantillonnage critique. L'analyse par ondelettes discrète à échantillonnage critique est également connue sous le nom d'analyse par ondelettes discrète décimée. L'analyse par ondelettes discrète décimée est celle qui convient le mieux pour la compression des données, le débruitage et la représentation parcimonieuse de certaines catégories de signaux et d'images.

Dans l'analyse par ondelettes discrète décimée, les échelles et les translations sont dyadiques.

Débruitage par ondelettes 1-D

Cet exemple montre comment débruiter un signal en utilisant l'analyse par ondelettes discrète.

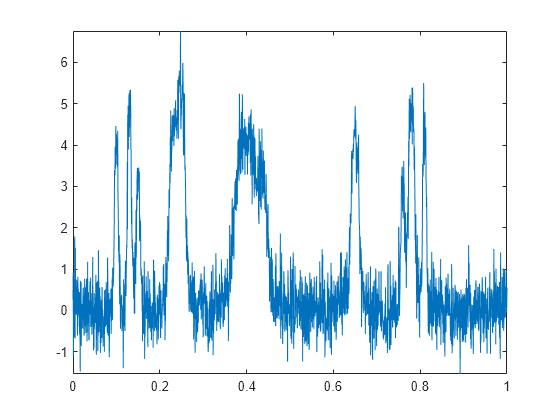
Créez un signal de référence.

len = 2^11;
h = [4  -5  3  -4  5  -4.2   2.1   4.3  -3.1   5.1  -4.2];
t = [0.1  0.13  0.15  0.23  0.25  0.40  0.44  0.65  0.76  0.78  0.81];
h  = abs(h);
w  = 0.01*[0.5 0.5 0.6 1 1 3 1 1 0.5 0.8 0.5];
tt = linspace(0,1,len);
xref = zeros(1,len);
for j=1:11
    xref = xref+(h(j)./(1+((tt-t(j))/w(j)).^4));
end

Ajoutez un bruit blanc gaussien de moyenne nulle avec une variance de 0,25.

rng default
x = xref + 0.5*randn(size(xref));
plot(x)
axis tight

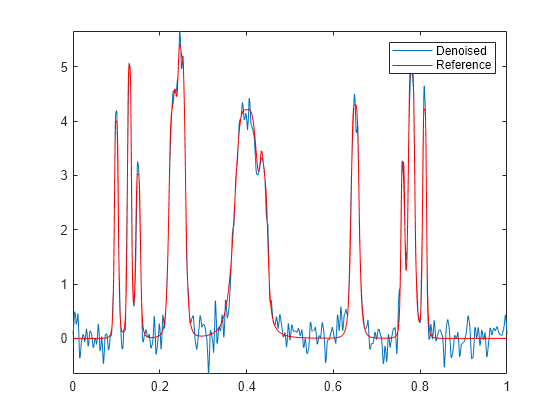
Débruitez le signal jusqu'au niveau 3 en utilisant l'ondelette la moins asymétrique de Daubechies avec 4 moments de fuite. Utilisez la règle de sélection du seuil universel de Donoho et Johnstone avec un seuillage doux basé sur les coefficients DWT au niveau 1. Utilisez le mode d'extension du signal de périodisation - dwtmode('per'). Tracez le résultat avec le signal de référence pour comparaison.

origmode = dwtmode('status','nodisplay');
dwtmode('per','nodisplay')
xd = wdenoise(x,3,'Wavelet','sym4',...
    'DenoisingMethod','UniversalThreshold','NoiseEstimate','LevelIndependent');
plot(xd)
axis tight
hold on
plot(xref,'r')
legend('Denoised','Reference')

Rétablissez le mode d'extension original.

dwtmode(origmode,'nodisplay')

Analyse par ondelettes discrète décimée 2-D

Cet exemple montre comment obtenir la DWT 2-D d'une image d'entrée.

Chargez et affichez l'image. L'image se compose de motifs verticaux, horizontaux et diagonaux.

load tartan;
imagesc(X); colormap(gray);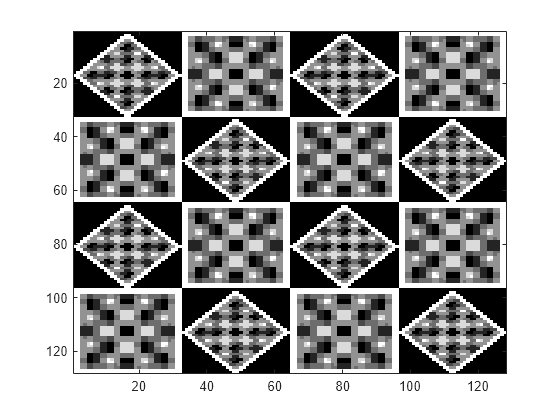

Obtenez la DWT 2-D au niveau 1 en utilisant l'ondelette biorthogonale B-spline et des filtres d'échelle avec 2 moments de fuite dans les filtres d'analyse et 4 moments de fuite dans les filtres de synthèse. Extrayez les coefficients d'ondelettes horizontaux, verticaux et diagonaux et les coefficients d'approximation. Affichez les résultats.

[C,S] = wavedec2(X,1,'bior2.4');
[H,V,D] = detcoef2('all',C,S,1);
A = appcoef2(C,S,'bior2.4');
subplot(221);
imagesc(A); title('Approximation Level 1');
colormap(gray);
subplot(222);
imagesc(H); title('Horizontal Details');
subplot(223);
imagesc(V); title('Vertical Details');
subplot(224);
imagesc(D); title('Diagonal Details');

Vous voyez que les détails des ondelettes sont sensibles aux orientations particulières de l'image d'entrée. Les coefficients d'approximation sont une approximation passe-bas de l'image originale.

Analyse par ondelettes discrète non décimée

Cet exemple montre comment obtenir la transformée en ondelettes non décimée (stationnaire) d'un signal bruité modulé en fréquence.

Chargez le signal Doppler bruité et obtenez la transformée en ondelettes stationnaires jusqu'au niveau 4.

load noisdopp
swc = swt(noisdopp,4,'sym8');

Tracez le signal original et les coefficients d'ondelettes de niveaux 1 et 3. Tracez l'approximation de niveau 4.

subplot(4,1,1)
plot(noisdopp)
subplot(4,1,2)
plot(swc(1,:))
ylabel('D1')
set(gca,'ytick',[])
subplot(4,1,3)
plot(swc(3,:))
ylabel('D3')
set(gca,'ytick',[])
subplot(4,1,4)
plot(swc(5,:))
ylabel('A4')
set(gca,'ytick',[])

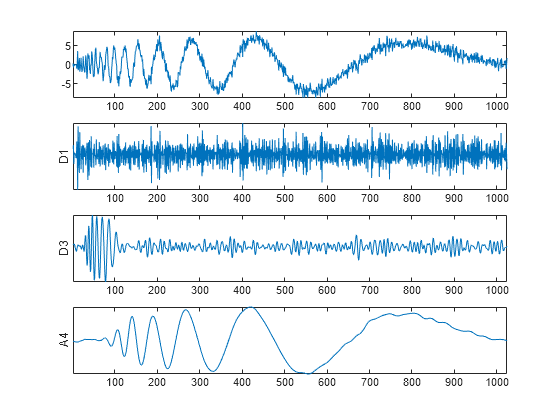
Les coefficients d'ondelette et d'approximation à chaque niveau sont de longueur égale au signal d'entrée. Le bruit additif est presque entièrement localisé dans les coefficients de détail de niveau un. Les coefficients de détail de niveau 3 capturent les oscillations à haute fréquence au début du signal Doppler. Les coefficients d'approximation de niveau 4 sont une approximation passe-bas du signal Doppler.

Obtenez la transformée en ondelettes 2-D non décimée d'une image. Utilisez l'ondelette la moins asymétrique de Daubechies, sym4, et obtenez l'analyse multirésolution jusqu'au niveau 3. Chargez l'image. Utilisez wcodemat pour mettre la matrice à l'échelle pour l'affichage.

load tartan
nbcol = size(map,1);
cod_X = wcodemat(X,nbcol);

Obtenez l'analyse multirésolution non décimée jusqu'au niveau 3.

[ca,chd,cvd,cdd] = swt2(X,3,'sym4');

Affichez l'image originale et les coefficients d'approximation et de détails à chaque niveau.

figure
subplot(2,2,1)
image(cod_X)
title('Original Image')
colormap(map)

for k = 1:3
    cod_ca  = wcodemat(ca(:,:,k),nbcol);
    cod_chd = wcodemat(chd(:,:,k),nbcol);
    cod_cvd = wcodemat(cvd(:,:,k),nbcol);
    cod_cdd = wcodemat(cdd(:,:,k),nbcol);
    decl = [cod_ca,cod_chd;cod_cvd,cod_cdd];
    
    subplot(2,2,k+1)
    image(decl)
    
    title(['SWT: Approx. ', ...
        'and Det. Coefs (Lev. ',num2str(k),')'])
    colormap(gray)
end

Voir aussi

wavedec | wavedec2 | wdenoise | wdenoise2 | swt | swt2 | modwt | modwtmra | dwtfilterbank

×

Ouvrir l'exemple

Vous possédez une version modifiée de cet exemple. Souhaitez-vous ouvrir cet exemple avec vos modifications ?

Non, écraser la version modifiée Oui