La traduction de cette page n'est pas à jour. Cliquez ici pour voir la dernière version en anglais.

Transformée en ondelettes continue et transformée en ondelettes continue inverse

Cet exemple montre comment utiliser la transformée en ondelettes continue (CWT) et la CWT inverse.

CWT des ondes sinusoïdales et des impulsions

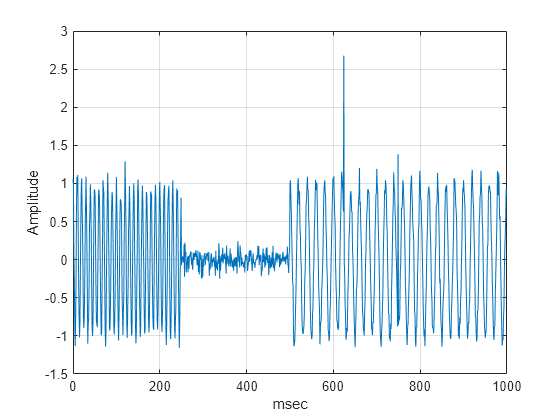
Créez et tracez un signal composé de deux ondes sinusoïdales disjointes de fréquences 100 et 50 Hz ponctuées de deux impulsions. La fréquence d'échantillonnage est de 1 kHz et la durée totale du signal est d'une seconde. L'onde sinusoïdale de 100 Hz se produit sur les 250 premières millisecondes des données. La sinusoïde de 50 Hz se produit sur les 500 dernières millisecondes. Les impulsions se produisent à 650 et 750 millisecondes. Le signal comporte également un bruit blanc gaussien additif de $N (0, 0.1^{2})$ . L'impulsion à 650 millisecondes est visible, mais l'impulsion à 750 millisecondes n'apparaît pas clairement dans les données du domaine temporel.

Fs = 1000;
t = 0:1/Fs:1-1/Fs;
x = zeros(size(t));
x([625,750]) = 2.5;
x = x+ cos(2*pi*100*t).*(t<0.25)+cos(2*pi*50*t).*(t>=0.5)+...
    0.1*randn(size(t));
plot(t.*1000,x)
grid on;
xlabel('msec'); ylabel('Amplitude');

Figure contains an axes object. The axes object with xlabel msec, ylabel Amplitude contains an object of type line.

Obtenez et tracez la CWT en utilisant l'ondelette de Morse analytique par défaut.

[cfs,f] = cwt(x,1000);
contour(t.*1000,f,abs(cfs));
xlabel('msec'); ylabel('Hz');
grid on;

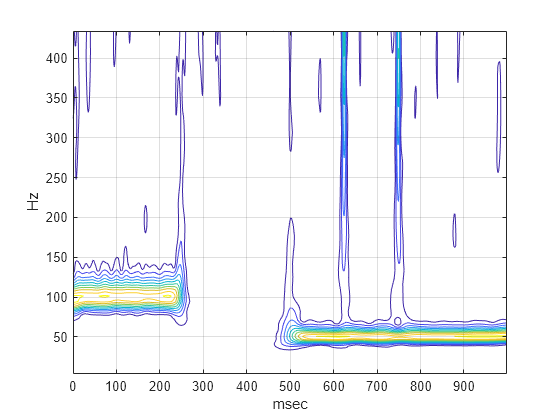
Figure contains an axes object. The axes object with xlabel msec, ylabel Hz contains an object of type contour.

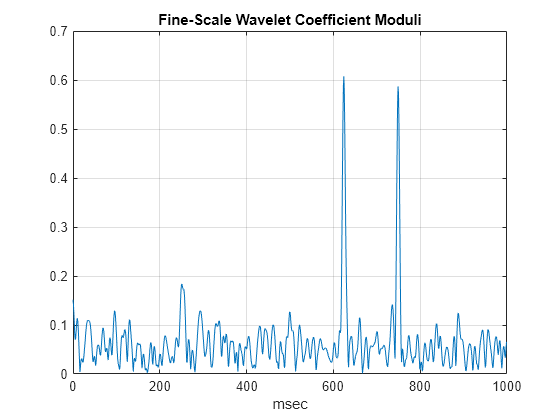
Les modules CWT montrent correctement les supports des sinusoïdes disjointes et les emplacements des impulsions à 650 et 750 millisecondes. Dans les modules CWT, l'impulsion à 750 millisecondes est clairement visible. C'est particulièrement vrai si vous ne tracez que les coefficients d'ondelettes les plus fins.

plot(t.*1000,abs(cfs(1,:)))
grid on
title('Fine-Scale Wavelet Coefficient Moduli')
xlabel('msec')

Figure contains an axes object. The axes object with title Fine-Scale Wavelet Coefficient Moduli, xlabel msec contains an object of type line.

CWT inverse localisée en fréquence

En utilisant la CWT inverse, vous pouvez construire des approximations localisées en fréquence pour les événements de votre série temporelle. Utilisez la CWT inverse pour obtenir une approximation de la sinusoïde de 100 Hz de l'exemple précédent.

xrec = icwt(cfs,[],f,[90 110]);
plot(t,x);
hold on;
plot(t,xrec,'r');
legend('Original Signal','Inverse CWT Approximation',...
    'Location','NorthEast');
grid on;

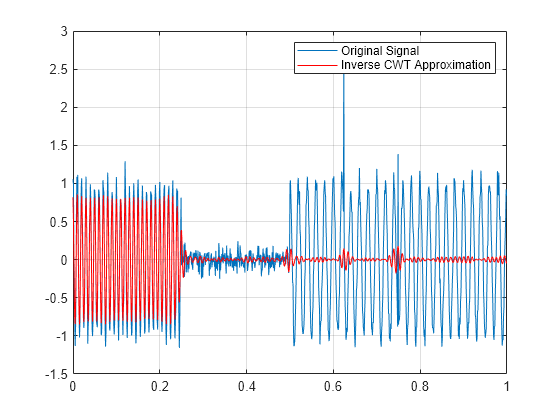
Figure contains an axes object. The axes object contains 2 objects of type line. These objects represent Original Signal, Inverse CWT Approximation.

Si vous zoomez sur le tracé, vous voyez que la composante 100-Hz est bien approximée mais que la composante 50-Hz a été supprimée.