About Wavelet Packet Analysis
Wavelet Toolbox™ software contains functions that let you
Examine and explore characteristics of individual wavelet packets
Perform wavelet packet analysis of 1-D and 2-D data
Use wavelet packets to compress and remove noise from signals and images
For more background on the wavelet packets, see the section Wavelet Packets.
Some object-oriented programming features are used for wavelet packet tree structures. For more detail, refer to Introduction to Object-Oriented Features.
This chapter takes you through the features of 1-D and 2-D wavelet packet analysis using the Wavelet Toolbox software. You'll learn how to
Load a signal or image
Perform a wavelet packet analysis of a signal or image
Compress a signal
Remove noise from a signal
Compress an image
Show statistics and histograms
The toolbox provides these functions for wavelet packet analysis. For more information, see the reference pages. The reference entries for these functions include examples showing how to perform wavelet packet analysis via the command line.
More examples can be found in the section Examples Using Wavelet Packet Tree Objects.
Analysis-Decomposition Functions
Synthesis-Reconstruction Functions
Decomposition Structure Utilities
Denoising and Compression
In the wavelet packet framework, compression and denoising ideas are exactly the same as those developed in the wavelet framework. The only difference is that wavelet packets offer a more complex and flexible analysis, because in wavelet packet analysis, the details as well as the approximations are split.
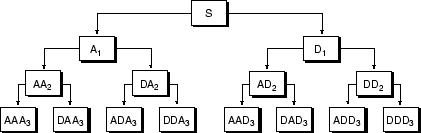
A single wavelet packet decomposition gives a lot of bases from which you can look for the best representation with respect to a design objective. This can be done by finding the “best tree” based on an entropy criterion.
Denoising and compression are interesting applications of wavelet packet analysis. The wavelet packet denoising or compression procedure involves four steps:
Decomposition
For a given wavelet, compute the wavelet packet decomposition of signal
xat levelN.Computation of the best tree
For a given entropy, compute the optimal wavelet packet tree. Of course, this step is optional. The graphical tools provide a Best Tree button for making this computation quick and easy.
Thresholding of wavelet packet coefficients
For each packet (except for the approximation), select a threshold and apply thresholding to coefficients.
Reconstruction
Compute wavelet packet reconstruction based on the original approximation coefficients at level
Nand the modified coefficients.