What Is System Identification Toolbox?
System Identification Toolbox™ provides MATLAB® functions, Simulink® blocks, and an app for dynamic system modeling, time-series analysis, and forecasting. You can learn dynamic relationships among measured variables to create transfer functions, process models, and state-space models in either continuous or discrete time while using time- or frequency-domain data. You can forecast time series using AR, ARMA, and other linear and nonlinear autoregressive modeling techniques.
The toolbox lets you estimate nonlinear system dynamics using Hammerstein-Wiener and nonlinear ARX models with machine learning techniques such as Gaussian processes (GP), support vector machines (SVM), and other representations. Alternatively, you can create neural ordinary differential equation (ODE) models using deep learning to capture nonlinear system dynamics. The toolbox lets you perform grey-box system identification for estimating parameters of a user-defined model. You can integrate identified models into Simulink for rapid simulations to enable control design and diagnostic and prognostic applications.
You can perform online parameter and state estimation using extended or unscented Kalman filters and particle filters for adaptive control, fault detection, and soft sensing applications. The toolbox lets you generate C/C++ code for online estimation algorithms to target embedded devices.
Published: 19 Oct 2022
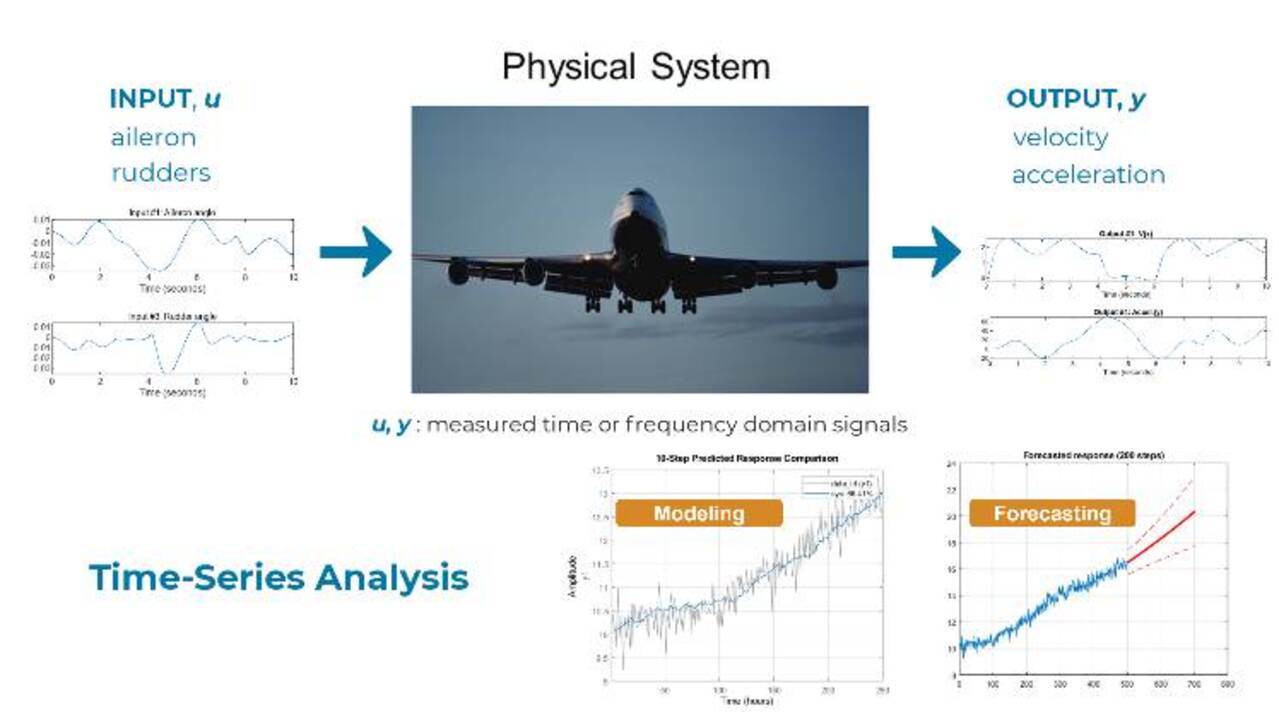
System Identification Toolbox lets you construct linear and nonlinear models of physical systems from measured time and frequency domain data, when the systems are not easily modeled from first principles or specifications. The toolbox also supports time-series data modeling for forecasting, analysis, and feature generation.
You can estimate many types of linear parametric models including transfer functions, state-space models, process models, and common polynomial models. For some of these model types, System Identification Toolbox can help you select model order to achieve the optimal trade-off between model fidelity and model complexity.
You can also create nonlinear models such as nonlinear ARX and Hammerstein-Wiener models. Using these models, you can represent nonlinearities that capture realistic effects of your system like saturation or learn nonlinearities using machine learning techniques such as SVMs, GPs, and regression tree ensembles. You can use your knowledge of the physics of your system to select regressors and fix the linear part of the nonlinear model. You can also create deep learning based nonlinear state space models using neural ODE for applications such as reduced order modeling, without having to write complicated code.
For systems whose dynamics change over time during their operation, you can perform online parameter and state estimation using recursive algorithms, and linear and nonlinear Kalman filters. You can use these online models for applications such as adaptive control, fault detection, and soft sensing.
You can use your identified models as plant models for control design and analysis with other tools and techniques such as Linear System Analyzer, PID tuner, and model predictive controllers. You can incorporate Identified models, state estimators, and recursive models into your Simulink simulations. The toolbox also supports code generation for identified models and online estimation algorithms for hardware-in-the-loop testing and deployment to embedded devices. You can also deploy model estimation algorithms using MATLAB compiler.
In addition to control design workflows, you can use System Identification Toolbox for modeling and forecasting time-series data, i.e. data that contains only measured output with no measured input, for applications such as modal or vibrational analysis, and diagnostics and prognostics.
For more information on the System Identification Toolbox, return to the product page.