Décomposition en modes empiriques
La décomposition en modes empiriques (Empirical Mode Decomposition ou EMD) est une technique multirésolution adaptative permettant de décomposer un signal en composantes physiques significatives. La technique EMD peut être utilisée pour analyser des signaux non stationnaires et non linéaires en les séparant en composants sur différentes résolutions. Certaines des applications courantes de la décomposition en modes empiriques concernent les applications de détection de défauts sur des roulements, d'analyse des données biomédicales, d'analyse des signaux de puissance et des signaux sismiques.
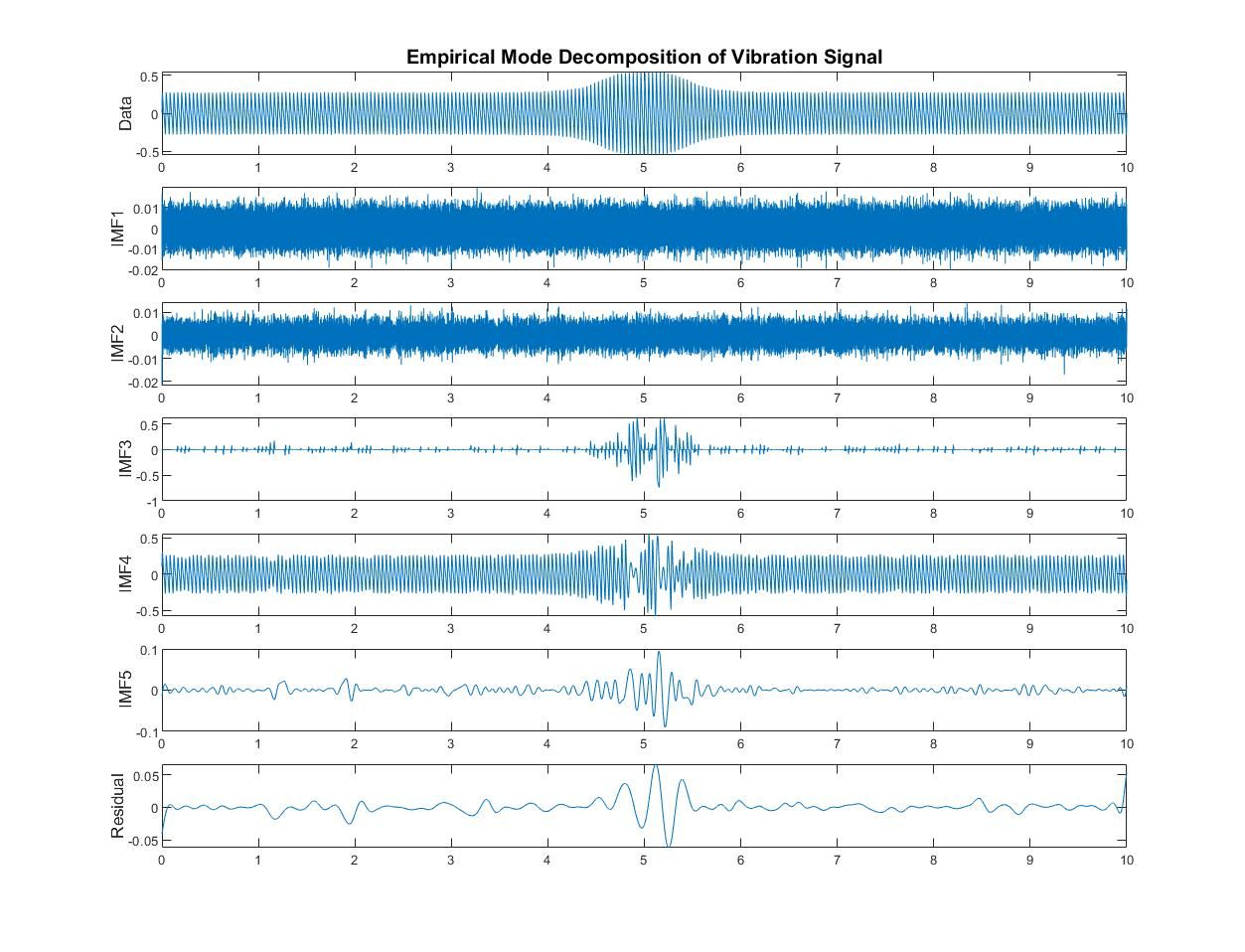
Signal de vibration analysé dans MATLAB avec la décomposition en modes empiriques (Exemple de code MATLAB)
La décomposition en modes empiriques peut être utilisée pour effectuer l'analyse temps-fréquence tout en restant dans le domaine temporel. Les composants sont dans la même échelle temps que le signal d'origine, ce qui les rend plus faciles à analyser. Contrairement à d'autres techniques d'analyse multirésolution (multiresolution analysis ou MRA), comme par exemple l'analyse par ondelettes, la décomposition en modes empiriques extrait de manière récursive différentes résolutions directement à partir des données sans utiliser de filtre ou de fonction fixe.
Une autre manière d'expliquer la technique EMD consiste à considérer un signal comme une oscillation rapide superposée à une oscillation plus lente. Une fois l'oscillation rapide extraite, l'algorithme EMD traite la composante restante plus lente en tant que nouveau signal et l'interprète de nouveau sous la forme d'une oscillation rapide superposée à une oscillation plus lente. L'algorithme s'exécute jusqu'à ce que le critère de sortie soit satisfait. Les composantes dans la technique EMD sont appelés des fonctions modes intrinsèques (intrinsic mode functions ou IMF).

Un signal sismique analysé et reconstruit avec des composantes sélectionnées avec l'application Signal Multiresolution Analyzer dans MATLAB.
La technique EMD permet d'éliminer des composantes spécifiques, comme par exemple le bruit, et de reconstruire le signal. Vous pouvez aussi extraire des composantes pertinentes pour effectuer des analyses plus approfondies.
Wavelet Toolbox™ et Signal Processing Toolbox™, utilisées avec MATLAB®, permettent de disposer de la technique EMD et d'autres techniques d'analyse multirésolution adaptatives. Ces techniques sont accessibles depuis l'application Signal Multiresolution Analyzer. Cette application simplifie la comparaison des résultats d'une technique à l'autre.
Exemples et démonstrations
Références logicielles
Voir aussi: transformée en ondelettes, vidéos sur les transformées en ondelettes, Signal Processing Toolbox, DSP System Toolbox™
