Flying Quality Analysis for 6DOF De Havilland Beaver Airframe
This example shows how to use eigenvalue analysis to determine the longitudinal flying quality characteristics (long-period phugoid mode and short-period mode) and lateral-directional flying quality characteristics (dutch roll mode, roll mode, and spiral mode) for an airframe modeled in Simulink®.
This example uses a linearized representation of the airframe dynamics for a trimmed flight condition for the flying quality analysis for a dynamic system (aircraft). The analysis is divided into longitudinal and lateral-directional motion. Longitudinal motion refers to motion in which the body changes position. The orientation is limited to the following 3 degrees of freedom: forward/backward (surge) translation, up/down (heave) translation, and pitch rotation. Lateral-directional motion refers to changes in position and orientation, which is limited to the remaining 3 degrees of freedom, left/right (sway) translation, roll rotation, and yaw rotation. In this example, Simulink Control Design™ functions are used to generate a trimmed operating point and to derive a linear state-space model for that operating point directly from a nonlinear Simulink model. From that state space model, the example directly computes longitudinal and lateral-directional flight modes and compares them against MIL-F-8785C Requirements.
To perform this analysis on an airframe of your own, use the Aerospace Blockset™ Flight Control Analysis Tools.
Create New Vehicle Model from Template
Create and open a new airframe model using the Aerospace Blockset 6DOF Airframe Template. When the project is loaded, an architecture model for an airframe and vehicle configuration data, environmental constants, and initial conditions are loaded to the model workspace.
dhbModel = 'DehavillandBeaverFlyingQualities'; if ~bdIsLoaded(dhbModel) open_system(new_system(dhbModel,'FromTemplate',... 'asb6DOFAirframeTemplate.sltx')); end


Specify a Desired Trim Condition
Next, define a trim condition around which to linearize the model. Set the position component Xe to a non-steady state and define non-zero initial conditions where applicable.
dhbOpSpec = operspec(dhbModel);

for idx = 13:numel(dhbOpSpec.States) % Set Environment States to non-steady state for jdx = 1:numel(dhbOpSpec.States(idx).SteadyState) dhbOpSpec.States(idx).SteadyState(jdx) = 0; end end dhbOpSpec.States(2).x = state.Theta; % theta dhbOpSpec.States(3).Known = 1; % psi dhbOpSpec.States(4).x = state.P; % p dhbOpSpec.States(5).x = state.Q; % q dhbOpSpec.States(6).x = state.R; % r dhbOpSpec.States(7).x = state.U; % U dhbOpSpec.States(8).x = state.V; % V dhbOpSpec.States(9).x = state.W; % W dhbOpSpec.States(10).x = state.XN; % Xe dhbOpSpec.States(10).SteadyState = 0; dhbOpSpec.States(11).x = state.XE; % Ye dhbOpSpec.States(12).x = state.XD; % Ze dhbOpSpec.States(12).Known = 1; dhbOpSpec.Inputs(2).Min = aircraft.Surfaces(1).Surfaces(1).MinimumValue; % elevator input min dhbOpSpec.Inputs(2).Max = aircraft.Surfaces(1).Surfaces(1).MaximumValue; % elevator input max dhbOpSpec.Inputs(1).Min = aircraft.Surfaces(2).Surfaces(1).MinimumValue; % aileron input min dhbOpSpec.Inputs(1).Max = aircraft.Surfaces(2).Surfaces(1).MaximumValue; % aileron input max dhbOpSpec.Inputs(3).Min = aircraft.Surfaces(3).Surfaces(1).MinimumValue; % rudder input min dhbOpSpec.Inputs(3).Max = aircraft.Surfaces(3).Surfaces(1).MaximumValue; % rudder input max
Create an Operating Point
Use findop() to find an operating point that satisfies the trim constraints defined above. View the Operating Point Search Report that is printed by this function below. Note that the defined specifications were successfully met.
dhbOpTrim = trimAirframe(dhbModel, dhbOpSpec)
Operating point search report: ---------------------------------
opreport =
Operating point search report for the Model DehavillandBeaverFlyingQualities.
(Time-Varying Components Evaluated at time t=0)
Operating point specifications were successfully met.
States:
----------
Min x Max dxMin dx dxMax
___________ ___________ ___________ ___________ ___________ ___________
(1.) phi
-Inf 0.0092342 Inf 0 4.3624e-21 0
(2.) theta
-Inf 0.29658 Inf 0 1.3074e-21 0
(3.) psi
0 0 0 0 -9.0144e-20 0
(4.) p
-Inf 3.0707e-20 Inf 0 1.9648e-10 0
(5.) q
-Inf 5.1124e-22 Inf 0 -3.2723e-09 0
(6.) r
-Inf -8.6217e-20 Inf 0 3.4405e-10 0
(7.) U
-Inf 33.0529 Inf 0 -2.1658e-09 0
(8.) V
-Inf 0.093272 Inf 0 -2.1775e-10 0
(9.) W
-Inf 10.1004 Inf 0 6.469e-09 0
(10.) Xe
-Inf -2.8165e-12 Inf -Inf 34.5619 Inf
(11.) Ye
-Inf 4.3033e-12 Inf 0 2.0002e-10 0
(12.) Ze
-2202 -2202 -2202 0 1.3464e-08 0
(13.) DehavillandBeaverFlyingQualities/Environment Model/Dryden Wind Turbulence Model (Continuous (+q +r))/Filters on angular rates/Hpgw/pgw_p
-Inf 0 Inf -Inf 0 Inf
-Inf 0 Inf -Inf 0 Inf
(14.) DehavillandBeaverFlyingQualities/Environment Model/Dryden Wind Turbulence Model (Continuous (+q +r))/Filters on angular rates/Hqgw/qgw_p
-Inf 0 Inf -Inf 0 Inf
-Inf 0 Inf -Inf 0 Inf
(15.) DehavillandBeaverFlyingQualities/Environment Model/Dryden Wind Turbulence Model (Continuous (+q +r))/Filters on angular rates/Hrgw/rgw_p
-Inf 0 Inf -Inf 0 Inf
-Inf 0 Inf -Inf 0 Inf
(16.) DehavillandBeaverFlyingQualities/Environment Model/Dryden Wind Turbulence Model (Continuous (+q +r))/Filters on velocities/Hugw(s)/ug_p
-Inf 0 Inf -Inf 0 Inf
-Inf 0 Inf -Inf 0 Inf
(17.) DehavillandBeaverFlyingQualities/Environment Model/Dryden Wind Turbulence Model (Continuous (+q +r))/Filters on velocities/Hvgw(s)/vg_p1
-Inf 0 Inf -Inf 0 Inf
-Inf 0 Inf -Inf 0 Inf
(18.) DehavillandBeaverFlyingQualities/Environment Model/Dryden Wind Turbulence Model (Continuous (+q +r))/Filters on velocities/Hvgw(s)/vgw_p2
-Inf 0 Inf -Inf 0 Inf
-Inf 0 Inf -Inf 0 Inf
(19.) DehavillandBeaverFlyingQualities/Environment Model/Dryden Wind Turbulence Model (Continuous (+q +r))/Filters on velocities/Hwgw(s)/wg_p1
-Inf 5.1038e-14 Inf -Inf 0 Inf
-Inf 0 Inf -Inf 0 Inf
(20.) DehavillandBeaverFlyingQualities/Environment Model/Dryden Wind Turbulence Model (Continuous (+q +r))/Filters on velocities/Hwgw(s)/wg_p2
-Inf 0 Inf -Inf 0 Inf
-Inf 0 Inf -Inf 0 Inf
Inputs:
----------
Min u Max
_________ _________ _________
(1.) DehavillandBeaverFlyingQualities/AileronCmd
-0.5236 0.0013469 0.5236
(2.) DehavillandBeaverFlyingQualities/ElevatorCmd
-0.5236 -0.14185 0.5236
(3.) DehavillandBeaverFlyingQualities/RudderCmd
-1.0472 -0.03733 1.0472
Outputs:
----------
Min y Max
___________ ___________ ___________
(1.) DehavillandBeaverFlyingQualities/StatesOut
-Inf -2.8165e-12 Inf
-Inf -2202 Inf
-Inf 0.29658 Inf
-Inf 33.0529 Inf
-Inf 10.1004 Inf
-Inf 5.1124e-22 Inf
-Inf -3.2723e-09 Inf
-Inf -2.1658e-09 Inf
-Inf 6.469e-09 Inf
-Inf 4.3033e-12 Inf
-Inf 0.0092342 Inf
-Inf 0 Inf
-Inf 0.093272 Inf
-Inf 3.0707e-20 Inf
-Inf -8.6217e-20 Inf
-Inf 1.9648e-10 Inf
-Inf 3.4405e-10 Inf
-Inf -2.1775e-10 Inf

dhbOpTrim =
Operating point for the Model DehavillandBeaverFlyingQualities.
(Time-Varying Components Evaluated at time t=0)
States:
----------
x
___________
(1.) phi
0.0092342
(2.) theta
0.29658
(3.) psi
0
(4.) p
3.0707e-20
(5.) q
5.1124e-22
(6.) r
-8.6217e-20
(7.) U
33.0529
(8.) V
0.093272
(9.) W
10.1004
(10.) Xe
-2.8165e-12
(11.) Ye
4.3033e-12
(12.) Ze
-2202
(13.) DehavillandBeaverFlyingQualities/Environment Model/Dryden Wind Turbulence Model (Continuous (+q +r))/Filters on angular rates/Hpgw/pgw_p
0
0
(14.) DehavillandBeaverFlyingQualities/Environment Model/Dryden Wind Turbulence Model (Continuous (+q +r))/Filters on angular rates/Hqgw/qgw_p
0
0
(15.) DehavillandBeaverFlyingQualities/Environment Model/Dryden Wind Turbulence Model (Continuous (+q +r))/Filters on angular rates/Hrgw/rgw_p
0
0
(16.) DehavillandBeaverFlyingQualities/Environment Model/Dryden Wind Turbulence Model (Continuous (+q +r))/Filters on velocities/Hugw(s)/ug_p
0
0
(17.) DehavillandBeaverFlyingQualities/Environment Model/Dryden Wind Turbulence Model (Continuous (+q +r))/Filters on velocities/Hvgw(s)/vg_p1
0
0
(18.) DehavillandBeaverFlyingQualities/Environment Model/Dryden Wind Turbulence Model (Continuous (+q +r))/Filters on velocities/Hvgw(s)/vgw_p2
0
0
(19.) DehavillandBeaverFlyingQualities/Environment Model/Dryden Wind Turbulence Model (Continuous (+q +r))/Filters on velocities/Hwgw(s)/wg_p1
5.1038e-14
0
(20.) DehavillandBeaverFlyingQualities/Environment Model/Dryden Wind Turbulence Model (Continuous (+q +r))/Filters on velocities/Hwgw(s)/wg_p2
0
0
Inputs:
----------
u
_________
(1.) DehavillandBeaverFlyingQualities/AileronCmd
0.0013469
(2.) DehavillandBeaverFlyingQualities/ElevatorCmd
-0.14185
(3.) DehavillandBeaverFlyingQualities/RudderCmd
-0.03733
Linearize the Vehicle Model at a Trimmed Operating Point
Define a set of linear analysis points in the model. In this example, an input perturbation is applied to the Aileron, Elevator, Rudder, and Throttle Command Input ports. Output measurements are taken for states , , and .
io(1) = linio([dhbModel '/ElevatorCmd'], 1, 'input'); io(2) = linio([dhbModel '/AileronCmd'], 1, 'input'); io(3) = linio([dhbModel '/RudderCmd'], 1, 'input'); io(4) = linio([dhbModel '/6DOF EOM'], 1, 'output', [], 'p'); io(5) = linio([dhbModel '/6DOF EOM'], 1, 'output', [], 'q'); io(6) = linio([dhbModel '/6DOF EOM'], 1, 'output', [], 'r'); [~] = setlinio(dhbModel,io); % Linearize the airframe dhbLinSys = linearizeAirframe(dhbModel, dhbOpTrim)

dhbLinSys =
A =
U W q theta V p r phi
U 0.00745 0.3422 -10.29 -9.347 0.0002891 0 0.09327 0
W -0.2811 -0.9307 32.23 -2.856 0.0006505 -0.09327 0 -0.08631
q 0.04963 -0.1624 -2.241 0 0.0003388 -7.309e-20 -0.2069 0
theta 0 0 1 0 0 0 -0.009234 8.621e-20
V -0.003445 -0.00459 0 -0.02638 -0.1329 9.943 -32.59 9.346
p 0.000192 -5.787e-05 0.002573 0 -0.06176 -3.704 1.232 0
r -1.06e-05 -2.057e-06 0.1266 0 0.00398 -0.5424 -0.4194 0
phi 0 0 0.002822 -9.426e-20 0 1 0.3056 3.995e-22
B =
Aileron Elevator Rudder
U 0 0 0.2039
W 0 -2.381 0
q 0 -6.022 0
theta 0 0 0
V -0.177 0 1.621
p -4.28 0 0.2095
r -0.02396 0 -1.432
phi 0 0 0
C =
U W q theta V p r phi
p 0 0 0 0 0 1 0 0
q 0 0 1 0 0 0 0 0
r 0 0 0 0 0 0 1 0
D =
Aileron Elevator Rudder
p 0 0 0
q 0 0 0
r 0 0 0
Continuous-time state-space model.
Model Properties
View the linearization result first as a continuous-time transfer function:
dhbLinSysTF = tf(dhbLinSys)
dhbLinSysTF =
From input "Aileron" to output...
-4.28 s^7 - 15.92 s^6 - 42.31 s^5 - 23.95 s^4 - 11.73 s^3 - 2.218 s^2 - 0.7365 s + 0.04815
p: ---------------------------------------------------------------------------------------------
s^8 + 7.42 s^7 + 24.91 s^6 + 48.08 s^5 + 39.6 s^4 + 26.94 s^3 + 5.145 s^2 + 2.438 s + 0.05262
0.004897 s^6 - 0.5359 s^5 - 0.5795 s^4 - 0.0673 s^3 + 0.03212 s^2 + 0.003037 s - 0.001455
q: ---------------------------------------------------------------------------------------------
s^8 + 7.42 s^7 + 24.91 s^6 + 48.08 s^5 + 39.6 s^4 + 26.94 s^3 + 5.145 s^2 + 2.438 s + 0.05262
-0.02396 s^7 + 2.153 s^6 + 6.965 s^5 + 17.74 s^4 + 1.486 s^3 + 0.7177 s^2 - 0.002263 s - 0.1576
r: -----------------------------------------------------------------------------------------------
s^8 + 7.42 s^7 + 24.91 s^6 + 48.08 s^5 + 39.6 s^4 + 26.94 s^3 + 5.145 s^2 + 2.438 s + 0.05262
From input "Elevator" to output...
-0.01536 s^6 - 0.939 s^5 - 2.502 s^4 - 1.372 s^3 - 0.0289 s^2 + 0.01623 s - 3.446e-05
p: ---------------------------------------------------------------------------------------------
s^8 + 7.42 s^7 + 24.91 s^6 + 48.08 s^5 + 39.6 s^4 + 26.94 s^3 + 5.145 s^2 + 2.438 s + 0.05262
-6.022 s^7 - 30.81 s^6 - 43.76 s^5 - 36.56 s^4 - 16.06 s^3 - 1.838 s^2 - 0.03403 s + 1.041e-06
q: ----------------------------------------------------------------------------------------------
s^8 + 7.42 s^7 + 24.91 s^6 + 48.08 s^5 + 39.6 s^4 + 26.94 s^3 + 5.145 s^2 + 2.438 s + 0.05262
-0.7626 s^6 - 3.573 s^5 - 3.434 s^4 - 1.421 s^3 - 0.4758 s^2 - 0.04876 s + 0.0001128
r: ---------------------------------------------------------------------------------------------
s^8 + 7.42 s^7 + 24.91 s^6 + 48.08 s^5 + 39.6 s^4 + 26.94 s^3 + 5.145 s^2 + 2.438 s + 0.05262
From input "Rudder" to output...
0.2095 s^7 - 1.086 s^6 - 6.983 s^5 - 23.29 s^4 - 24.58 s^3 - 1.349 s^2 - 2.694 s + 0.2278
p: ---------------------------------------------------------------------------------------------
s^8 + 7.42 s^7 + 24.91 s^6 + 48.08 s^5 + 39.6 s^4 + 26.94 s^3 + 5.145 s^2 + 2.438 s + 0.05262
0.3069 s^6 + 1.51 s^5 + 1.523 s^4 + 0.524 s^3 + 0.1392 s^2 - 0.0004648 s - 0.006884
q: ---------------------------------------------------------------------------------------------
s^8 + 7.42 s^7 + 24.91 s^6 + 48.08 s^5 + 39.6 s^4 + 26.94 s^3 + 5.145 s^2 + 2.438 s + 0.05262
-1.432 s^7 - 10.13 s^6 - 30.55 s^5 - 50.66 s^4 - 18.97 s^3 - 12.41 s^2 - 1.833 s - 0.7455
r: ---------------------------------------------------------------------------------------------
s^8 + 7.42 s^7 + 24.91 s^6 + 48.08 s^5 + 39.6 s^4 + 26.94 s^3 + 5.145 s^2 + 2.438 s + 0.05262
Continuous-time transfer function.
Model Properties
Discussion of Coupling Between Longitudinal and Lateral-directional Modes
The A and B matrices of the state-space model above can be partitioned to separate the longitudinal and lateral states.

A Matrix Coupling
It is evident by the presence of non-zero terms in the upper-right and lower-left blocks of the A matrix that coupling between longitudinal and lateral-directional modes is present. The terms are small in magnitude compared to terms in the upper-left and lower-right blocks. Coupling is expected, and occurs when sideslip and roll angles are non-zero. The coupling effect is minimized in this example by defining a trim condition with a near-zero sideslip.
Given the small relative magnitude of the coupling terms in the A matrix, the rest of the example assumes that the longitudinal and lateral dynamic modes are decoupled and analyzes the longitudinal and lateral dynamics separately. However, it is important to note that in some cases, the coupling impact on the dynamic behavior cannot be ignored. Nonnegligible coupling terms can also be an indication that the selected trim condition is not suitable for linearization.
B Matrix Coupling
The B matrix can be partitioned to separate longitudinal (elevator) and lateral (aileron and rudder) controls inputs.
B = table(dhbLinSys.B(:,2), dhbLinSys.B(:,1), dhbLinSys.B(:,3), 'RowNames',dhbLinSys.StateName, 'VariableNames', [dhbLinSys.InputName(2); dhbLinSys.InputName([1,3])])
B=8×3 table
Elevator Aileron Rudder
________ _________ _______
U 0 0 0.20391
W -2.3806 0 0
q -6.0222 0 0
theta 0 0 0
V 0 -0.177 1.6214
p 0 -4.2797 0.20955
r 0 -0.023961 -1.432
phi 0 0 0
Note that the elevator has no effect on the lateral-directional states. The effects of aileron and rudder controls on the longitudinal states are minimal.
Visualize these relationships with step response plots. Notice the minimal coupling that exists between the longitudinal and lateral-directional states and controls.
step(dhbLinSysTF)

Reduce Combined State-Space Model to Decoupled Longitudinal Model
dhbLonLinSys = xelim(dhbLinSys, 5:8, 'Truncate')dhbLonLinSys =
A =
U W q theta
U 0.00745 0.3422 -10.29 -9.347
W -0.2811 -0.9307 32.23 -2.856
q 0.04963 -0.1624 -2.241 0
theta 0 0 1 0
B =
Aileron Elevator Rudder
U 0 0 0.2039
W 0 -2.381 0
q 0 -6.022 0
theta 0 0 0
C =
U W q theta
p 0 0 0 0
q 0 0 1 0
r 0 0 0 0
D =
Aileron Elevator Rudder
p 0 0 0
q 0 0 0
r 0 0 0
Continuous-time state-space model.
Model Properties
dhbLonLinSysTF = tf(dhbLonLinSys)
dhbLonLinSysTF =
From input "Aileron" to output...
p: 0
q: 0
r: 0
From input "Elevator" to output...
p: 0
-6.022 s^3 - 5.174 s^2 - 0.5809 s - 1.361e-17
q: -----------------------------------------------
s^4 + 3.164 s^3 + 7.903 s^2 + 0.5583 s + 0.9104
r: 0
From input "Rudder" to output...
p: 0
0.01012 s^2 + 0.01873 s - 7.807e-20
q: -----------------------------------------------
s^4 + 3.164 s^3 + 7.903 s^2 + 0.5583 s + 0.9104
r: 0
Continuous-time transfer function.
Model Properties
stepplot(dhbLonLinSys(2, 2))

Reduce Combined State-Space Model to Decoupled Lateral-Directional Model
dhbLatLinSys = xelim(dhbLinSys, 1:4, 'Truncate')dhbLatLinSys =
A =
V p r phi
V -0.1329 9.943 -32.59 9.346
p -0.06176 -3.704 1.232 0
r 0.00398 -0.5424 -0.4194 0
phi 0 1 0.3056 3.995e-22
B =
Aileron Elevator Rudder
V -0.177 0 1.621
p -4.28 0 0.2095
r -0.02396 0 -1.432
phi 0 0 0
C =
V p r phi
p 0 1 0 0
q 0 0 0 0
r 0 0 1 0
D =
Aileron Elevator Rudder
p 0 0 0
q 0 0 0
r 0 0 0
Continuous-time state-space model.
Model Properties
dhbLatLinSysTF = tf(dhbLatLinSys)
dhbLatLinSysTF =
From input "Aileron" to output...
-4.28 s^3 - 2.382 s^2 - 0.8421 s + 0.05288
p: -----------------------------------------------
s^4 + 4.256 s^3 + 3.514 s^2 + 2.642 s + 0.05849
q: 0
-0.02396 s^3 + 2.229 s^2 + 0.1039 s - 0.173
r: -----------------------------------------------
s^4 + 4.256 s^3 + 3.514 s^2 + 2.642 s + 0.05849
From input "Elevator" to output...
p: 0
q: 0
r: 0
From input "Rudder" to output...
0.2095 s^3 - 1.749 s^2 - 3.112 s + 0.2502
p: -----------------------------------------------
s^4 + 4.256 s^3 + 3.514 s^2 + 2.642 s + 0.05849
q: 0
-1.432 s^3 - 5.601 s^2 - 1.513 s - 0.8188
r: -----------------------------------------------
s^4 + 4.256 s^3 + 3.514 s^2 + 2.642 s + 0.05849
Continuous-time transfer function.
Model Properties
stepplot(dhbLatLinSys([1,3], [1,3]))

Discussion of Characteristic Equation Roots and Their Connection to Dynamic Stability
To determine if an airframe is dynamically stable at a particular operating point, examine the roots of the decoupled longitudinal and lateral-directional characteristic equations (separately). In general, the roots of both equations are of the form:
where and are real numbers. These roots characterize the modes of the system motion and are used in determining stability:
If is negative and is nonzero, the motion is a periodic damped oscillation, as seen here.
t = 0:.1:10; plot(t, exp(-.25*t).*sin(3*t)); ylabel('Displacement'); xlabel('Time (sec)'); title('Damped Oscillation');

If is positive and is nonzero, the motion is a periodic diverging oscillation.
plot(t, exp(.25*t).*sin(3*t)); ylabel('Displacement'); xlabel('Time (sec)'); title('Diverging Oscillation');

If is zero, the motion is aperiodic. It diverges if is positive and converges if is negative.
plot(t, exp(.25*t)); hold on; plot(t, exp(-.25*t)); legend('positive \eta', 'negative \eta'); hold off; ylabel('Displacement'); xlabel('Time (sec)'); title('Aperiodic Motion');

Analyze the Longitudinal Stability Characteristics of the Vehicle Model
This section demonstrates a longitudinal dynamic stability analysis. A more comprehensive longitudinal stability analysis and discussion is provided in the LongitudinalFlyingQuality3DOFAnalysisExample. This example highlights the results of that analysis.
Using the above criteria, it follows that any real root or real part of a root must be negative in order for the dynamic system to be stable. The roots of the longitudinal state-space model are:
dhbLonRoots = eig(dhbLonLinSys)
dhbLonRoots = 4×1 complex
-1.5698 + 2.2900i
-1.5698 - 2.2900i
-0.0122 + 0.3434i
-0.0122 - 0.3434i
Visualize these roots using a Zero-Pole Plot. As discussed, for inherent stability all roots should have negative real components.
pzplot(dhbLonLinSys,'b'); grid on;

Calculate Short-Period Mode Characteristics
We can compute the damping ratio and the undamped natural frequency of the short-period mode using the relationship:
Short-Period Mode Damping Ratio and Natural Frequency
dhbZeta_sp = sqrt(1/(1+(imag(dhbLonRoots(1))/real(dhbLonRoots(1)))^2))
dhbZeta_sp = 0.5654
dhbOmega_n_sp = -real(dhbLonRoots(1))/dhbZeta_sp
dhbOmega_n_sp = 2.7764
Time to Double the Short-Period Mode Amplitude
dhbT_2_sp = log(2)/(-dhbZeta_sp*dhbOmega_n_sp)
dhbT_2_sp = -0.4416
Note that the damping ratio is positive and the corresponding time-to-double is be negative. This means that in this case is representative of the time-to-halve the short-period mode amplitude, or .
Calculate Phugoid Mode Characteristics
We can compute the damping ratio and the undamped natural frequency of the phugoid mode using the relationship:
Phugoid Mode Damping Ratio and Natural Frequency
dhbZeta_ph = sqrt(1/(1+(imag(dhbLonRoots(3))/real(dhbLonRoots(3)))^2))
dhbZeta_ph = 0.0354
dhbOmega_n_ph = -real(dhbLonRoots(3))/dhbZeta_ph
dhbOmega_n_ph = 0.3437
Time to Double the Phugoid Mode Amplitude
dhbT_2_ph = log(2)/(-dhbZeta_ph*dhbOmega_n_ph)
dhbT_2_ph = -56.9741
Note that the damping ratio is positive and the corresponding time-to-double is be negative. This means that in this case is representative of the time-to-halve the phugoid mode amplitude, or .
Plot the Phugoid and Short-Period Responses
Observe that the short-period mode is much better damped than the phugoid mode.
Note the difference in time scales!
figure; subplot(2,1,1) t = 0:.1:500; plot(t, dhbOmega_n_ph/sqrt(1-dhbZeta_ph^2).*exp(-dhbZeta_ph*dhbOmega_n_ph*t).*sin(dhbOmega_n_ph*sqrt(1-dhbZeta_ph^2)*t)) ylabel('Displacement'); xlabel('Time (sec)'); title('Long-period (Phugoid) Response'); grid on; subplot(2,1,2) t = 0:.025:10; plot(t, dhbOmega_n_sp/sqrt(1-dhbZeta_sp^2).*exp(-dhbZeta_sp*dhbOmega_n_sp*t).*sin(dhbOmega_n_sp*sqrt(1-dhbZeta_sp^2)*t)) ylabel('Displacement'); xlabel('Time (sec)'); title('Short-period Response'); grid on

To quickly perform the longitudinal stability analysis use the computeLongitudinalFlyingQualities function.
longFlyingQual = computeLongitudinalFlyingQualities(dhbModel, dhbLinSys)
longFlyingQual = struct with fields:
PhugoidMode: [1×1 struct]
ShortPeriodMode: [1×1 struct]
phugoidModeStruct = longFlyingQual.PhugoidMode
phugoidModeStruct = struct with fields:
root: [2×1 double]
oscillatoryMode: 'Phugoid (Long-Period Mode)'
zeta: 0.0354
wn: 0.3437
T2: -56.9741
Tc: []
response: 'converging oscillatory motion'
description: 'complex conjugate pair with negative real components'
RequirementSource: "MIL-F-8785C"
RequirementName: "Phugoid Stability"
ID: "3.2.1.2"
FlyingQualityLevel: "2"
FlightPhase: "B"
AircraftClass: ["I" "II" "III" "IV"]
Verified: 1
MILF8785CRequirement: 'Satisfies MIL-F-8785C Level 2 Criteria (zeta_ph >= 0.0)'
Analyze the Lateral-directional Stability Characteristics of the Vehicle Model
(The analysis in this section can be performed using computeLateralDirectionalFlyingQualities(dhbModel, dhbLinSys).)
Using the above criteria, it follows that any real root or real part of a root must be negative in order for the dynamic system to be stable. The roots of the lateral-directional state-space model are:
dhbLatRoots = eig(dhbLatLinSys)
dhbLatRoots = 4×1 complex
-3.4601 + 0.0000i
-0.3867 + 0.7691i
-0.3867 - 0.7691i
-0.0228 + 0.0000i
Visualize these roots using a Zero-Pole Plot. As discussed, for inherent stability all roots should have negative real components.
figure; pzplot(dhbLatLinSys,'b'); grid on;
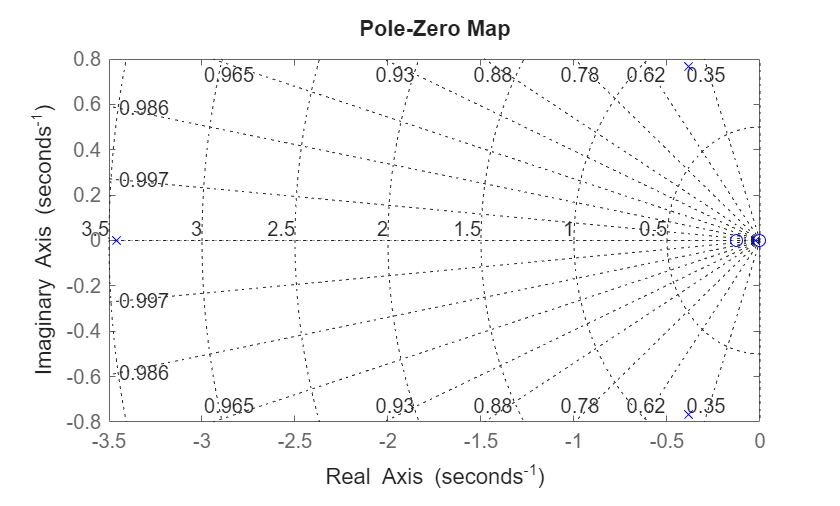
The roots are one pair of complex conjugates and two real roots. This is expected for inherently stable aircraft. The complex conjugate pair is the dutch roll mode. The slower real root with smaller magnitude is the spiral mode, and the remaining faster real root is the roll-subsidence mode. Compute the damping ratio and the undamped natural frequency of dutch roll mode, and the time constant and time to double amplitude of the roll and spiral modes using the following relationships:
and
,
,
Calculate Dutch Roll Mode Characteristics
Compute the damping ratio and the undamped natural frequency of the dutch roll mode using the relationship:
Dutch Roll Mode Damping Ratio
dhbZeta_dr = sqrt(1/(1+(imag(dhbLatRoots(2))/real(dhbLatRoots(2)))^2))
dhbZeta_dr = 0.4492
Dutch Roll Mode Undamped Natural Frequency
rad/s
dhbOmega_n_dr = -real(dhbLatRoots(2))/dhbZeta_dr
dhbOmega_n_dr = 0.8608
Time to Double the Dutch Roll Mode Amplitude
sec
dhbT_2_dr = log(2)/(-dhbZeta_dr*dhbOmega_n_dr)
dhbT_2_dr = -1.7925
Note that the dutch roll mode damping ratio is positive, so the time-to-double the dutch roll mode amplitude is negative. This means that represents the time-to-halve the dutch roll mode amplitude, or .
Calculate Spiral Mode Characteristics
Compute the time constant and time to double amplitude of the spiral mode using the relationships:
,
Spiral Mode Time Constant
sec
dhbTau_s = -1/dhbLatRoots(4)
dhbTau_s = 43.8378
Time to Double the Spiral Mode Amplitude
sec
dhbT_2_s = -log(2)*dhbTau_s
dhbT_2_s = -30.3861
Note that the time-to-double the spiral mode amplitude is negative. This means that represents the time-to-halve the spiral mode amplitude, or .
Calculate Roll-Subsidence Mode Characteristics
Compute the time constant and time to double amplitude of the roll mode using the relationships:
,
Roll Mode Time Constant
dhbTau_r = -1/dhbLatRoots(1)
dhbTau_r = 0.2890
Time to Double the Roll Mode Amplitude
dhbT_2_r = -log(2)*dhbTau_r
dhbT_2_r = -0.2003
Note that the time-to-double the roll mode amplitude is negative. This means that represents the time-to-halve the roll mode amplitude, or .
Visualize Dutch Roll Response
t = 0:.1:30; figure; plot(t, dhbOmega_n_dr/sqrt(1-dhbZeta_dr^2).*exp(-dhbZeta_dr*dhbOmega_n_dr*t).*sin(dhbOmega_n_dr*sqrt(1-dhbZeta_dr^2)*t)) ylabel('Displacement'); xlabel('Time (sec)'); title('Dutch Roll Response'); grid on; grid on;

Visualize Roll and Spiral Responses
Observe that the roll mode is much better damped than the spiral mode.
Note the difference in time scales!
figure; subplot(2,1,1) t = 0:.1:5; plot(t, 1/dhbTau_r*exp(-t/dhbTau_r)) ylabel('Displacement'); xlabel('Time (sec)'); title('Roll Subsidence Mode Response'); grid on; subplot(2,1,2)
t = 0:.1:300; plot(t, 1/dhbTau_s*exp(-t/dhbTau_s)) ylabel('Displacement'); xlabel('Time (sec)'); title('Spiral Mode Response'); grid on;

Quickly perform the lateral stability analysis using the computeLateralDirectionalFlyingQualities function.
latFlyingQual = computeLateralDirectionalFlyingQualities(dhbModel, dhbLinSys)
latFlyingQual = struct with fields:
DutchRollMode: [1×1 struct]
RollMode: [1×1 struct]
SpiralMode: [1×1 struct]
DutchRollModeStruct = latFlyingQual.DutchRollMode
DutchRollModeStruct = struct with fields:
root: [2×1 double]
oscillatoryMode: 'Dutch Roll Mode'
zeta: 0.4492
wn: 0.8608
T2: -1.7925
Tc: []
response: 'converging oscillatory motion'
description: 'complex conjugate pair with negative real components'
RequirementSource: "MIL-F-8785C"
RequirementName: "Lateral-Directional Oscillations (Dutch Roll)"
ID: "3.3.1.1"
FlyingQualityLevel: "1"
FlightPhase: "B"
AircraftClass: ["I" "II" "III" "IV"]
Verified: 1
MILF8785CRequirement: 'Satisfies MIL-F-8785C Level 1 Criteria (zeta_d >= 0.08, omega_n >= 0.4, zeta_d*omega_n_d >= 0.15)'
MIL-F-8785C Flying Quality Requirements
Flying quality requirements are presented for three levels of flying qualities. These flying quality levels, in decreasing order of desirability, are:
Level 1: Flying qualities clearly adequate to accomplish mission flight phase. Corresponds with Cooper-Harper Scale values 1-3.5.
Level 2: Flying qualities adequate to accomplish mission flight phase with some increase in pilot workload required or degradation in mission effectiveness. Corresponds with Cooper-Harper Scale values 3.5-6.5.
Level 3: Flying qualities adequate for airplane to be safely controlled, but excessive pilot workload is required or mission effectiveness is inadequate. Corresponds with Cooper-Harper Scale values 6.5-9+.
Note that airplanes must be designed to satisfy Level 1 requirements with all systems in their normal operating state.
Longitudinal Flying Quality Requirements
Phugoid Mode Damping Requirements
Per MIL-F-8785C, the long-period airspeed oscillations (phugoid) which occur when an airplane seeks a stabilized airspeed following a disturbance must meet the following minimum requirements:
Level 1:
Level 2:
Level 3: sec
where is the phugoid damping ratio and is the time-to-double the phugoid amplitude.
With , the phugoid mode for this aircraft is close, but does not meet Level 1 criteria of the MIL-F-8785C standard. The response however is damped (), and the phugoid mode meets Level 2 criteria.
Short-Period Mode Damping Requirements
MIL-F-8785C outlines upper and lower limits for the short-period damping ratio. If damping is too low, short-period response can produce troublesome oscillation, and if damping is too high, response to control inputs can be sluggish. The following requirements are for Flight Phase B (all airplane classes) as defined in MIL-F-8785C (non-terminal flight phases that are normally accomplished using gradual maneuvers - climb, cruise, loiter, descent, etc.):
Level 1:
Level 2:
Level 3:
where is the short-period damping ratio.
With , the short-period mode for this aircraft meets the Level 1 criteria of the MIL-F-8785C standard.
Lateral-Directional Flying Quality Requirements
Dutch Roll Mode Damping Requirements
Per MIL-F-8785C, the dutch roll undamped natural frequency and damping ratio should meet the following requirements. Note that Level 1 requirements in MIL-F-8785C are separated by flight phase and airplane class. The following requirements are for Flight Phase B (all airplane classes) as defined in MIL-F-8785C (non-terminal flight phases that are normally accomplished using gradual maneuvers - climb, cruise, loiter, descent, etc.):
Level 1:
rad/s
rad/s
Level 2:
rad/s
rad/s
Level 3:
rad/s
where is the dutch roll damping ratio and is the dutch roll natural frequency.
With , , and , the dutch roll mode for this aircraft meets the Level 1 criteria of the MIL-F-8785C standard.
Roll-Subsidence Mode Time Constant Requirements
MIL-F-8785C outlines the following maximum allowable roll-subsidence mode time constants. The roll-subsidence mode time constant is a measure of roll rate subsidence. A small time constant signifies a rapid decrease of roll rate following pilot-provided lateral control input. The following requirements are for Flight Phase B (all airplane classes) as defined in MIL-F-8785C (non-terminal flight phases that are normally accomplished using gradual maneuvers - climb, cruise, loiter, descent, etc.):
Level 1:
Level 2:
Level 3:
where is the roll-subsidence mode time constant.
With , the roll-subsidence mode for this aircraft meets the Level 1 criteria of the MIL-F-8785C standard.
Spiral Mode Time to Double Amplitude Requirements
While MIL-F-8785C does not provide specific damping requirements for the spiral mode, it does list limits for the allowable time to double amplitude of spiral mode divergence. The following requirements are for Flight Phase B (all airplane classes) as defined in MIL-F-8785C (non-terminal flight phases that are normally accomplished using gradual maneuvers - climb, cruise, loiter, descent, etc.):
Level 1:
Level 2:
Level 3:
where is the time to double the amplitude in the spiral mode. Note that if the spiral model root is negative, the aircraft is spiral mode stable, and the time to double the spiral model amplitude is negative. In this case represents the time-to-halve the spiral mode amplitude Because the requirements only provide guidance for aircraft with unstable spiral mode behavior, an aircraft with stable spiral mode response is deemed to meet MIL-F-8785C Level 1 Criteria in this section.
With , the spiral mode for this aircraft meets the Level 1 criteria of the MIL-F-8785C standard.
References
[1] Moorehouse, David J., Woodcock, Robert J., "Background Information and User Guide For MIL-F-8785C, Military Specification - Flying Qualities of Piloted Airplanes", AFWAL-TR-81-3109, July 1982.
[2] Roskam, J., "Airplane Flight Dynamics and Automatic Flight Controls (Part 1)", DAR Corporation, 2003.
[3] McCormick, B.W. "Aerodynamics, Aeronautics, and Flight Mechanics" 2rd Ed., John Wiley & Sons Inc., 1995.
[4] Stevens, Brian, and Frank Lewis, Aircraft Control and Simulation, Second Edition, John Wiley & Sons, 2003