Continuously Variable Transmission
Push belt continuously variable transmission with independent radii control
Libraries:
Powertrain Blockset /
Transmission /
Transmission Systems
Description
The Continuously Variable Transmission block implements a push belt continuously variable transmission (CVT) with independent radii control. Use the block for control system design, powertrain matching, and fuel economy studies. You can configure the block for internal or external control:
Internal — Input direction and pulley ratio requests
External — Input direction and pulley displacement requests
The table summarizes the pulley kinematic, speed reduction, and dynamic calculations made by the Continuously Variable Transmission block.
| Calculation | Pulley Kinematics | Reverse and Final Speed Reduction | Dynamics |
|---|---|---|---|
| Final angular speed ratio | ✓ | ✓ | ✓ |
| Belt torque applied to the secondary and primary pulleys | ✓ | ||
| Torque applied to the secondary and primary pulleys | ✓ | ||
| Angular velocity of secondary and primary pulleys | ✓ | ✓ | ✓ |
| Belt and pulley geometry | ✓ | ||
| Belt linear speed | ✓ | ||
| Wrap angle on secondary and primary pulley | ✓ | ||
| Primary and secondary pulley radii | ✓ |
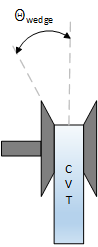
The figure shows the CVT variator with two configurations. In the first configuration, which illustrates speed reduction, the variator is set to decrease the primary pulley radius and increase the secondary pulley radius. In the second configuration, which illustrates overdrive, the variator is set to increase the primary pulley radius and decrease the secondary pulley radius.

Pulley Kinematics
Using the physical dimensions of the system, the block calculates the primary and secondary variator positions that meet the pulley ratio request.
The figure and equations summarize the geometric dependencies.
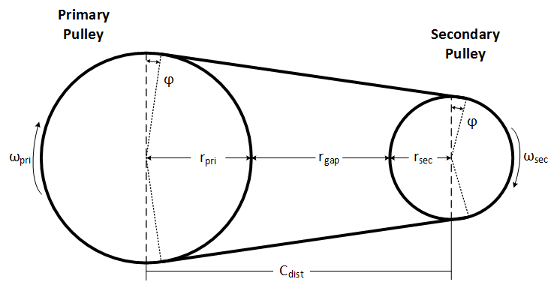
The equations use these variables.
| ratiorequest | Pulley gear ratio request |
| ratiocommand | Pulley gear ratio command, based on request and physical limitations |
| rgap | Gap distance between variator pulleys |
| Cdist | Distance between variator pulley centers |
| rpmax | Maximum variator primary pulley radius |
| rsmax | Maximum variator secondary pulley radius |
| rpmin | Minimum variator primary pulley radius |
| rsmin | Minimum variator secondary pulley radius |
| ro | Initial pulley radii with gear ratio of |
| Lo | Initial belt length, resulting from variator specification |
| xpri | Variator primary pulley displacement, resulting from controller request |
| xsec | Variator secondary pulley displacement, resulting from controller request |
| rpri | Variator primary pulley radius, resulting from controller request |
| rsec | Variator secondary pulley radius, resulting from controller request |
| Θwedge | Variator wedge angle |
| Φ | Angle of belt to pulley contact point |
| L | Belt length, resulting from variator position |
Reverse and Final Speed Reduction
The CVT input shaft connects to a planetary gear set that drives the primary pulley. The shift direction determines the input gear inertia, efficiency, and gear ratio. The shift direction is the filtered commanded direction:
For forward motion ():
For reverse motion ():
The gear ratio and efficiency determine the input drive shaft speed and torque applied to the primary pulley:
The block reduces the secondary pulley speed and applied torque using a fixed gear ratio.
The final gear ratio, without slip, is given by:
The equations use these variables.
| Ni | Input planetary gear ratio |
| Dir | CVT direction command |
| Dirshift | Direction used to determine planetary inertia, efficiency, and ratio |
| τs | Direction shift time constant |
| ηfwd, ηrev | Forward and reverse gear efficiency, respectively |
| Jfwd, Jrev | Forward and reverse gear inertia, respectively |
| Nrev | Reverse gear ratio |
| Tapp_pri, Tapp_sec | Torque applied to primary and secondary pulleys, respectively |
| Ti | Input drive shaft torque |
| ωi, ωo | Input and output drive shaft speed, respectively |
| ωpri, ωsec | Primary and secondary pulley speed, respectively |
| Nfinal | Total no-slip gear ratio |
Dynamics
The maximum torque that the CVT can transmit depends on the friction between the pulleys and belt. According to Prediction of Friction Drive Limit of Metal V-Belt, the torque friction is defined as:
Without macro slip, the tangential acceleration of the pulley is assumed to be equal to the belt acceleration. Once the torque reaches the static friction limit, the belt begins to slip, and the pulley and belt acceleration are independent. During slip, the torque transmitted by the belt is a function of the kinetic friction factor. During the transition from slip to non-slip conditions, the belt and tangential pulley velocities are equal.
The block implements these equations for four different slip conditions.
| Condition | Equations |
|---|---|
|
Belt slips on both secondary and primary pulleys |
|
|
Belt slips on only the primary pulley |
|
|
Belt slips on only the secondary pulley |
|
|
Belt does not slip |
|
|
Slip direction |
|
The equations use these variables.
| TBoP_pri, TBoP_sec | Belt torque acting on the primary and secondary pulleys, respectively |
| Tapp_pri, Tapp_sec | Torque applied to primary and secondary pulleys, respectively |
| Jpri, Jsec | Primary and secondary pulley rotational inertias, respectively |
| bpri, bsec | Primary and secondary pulley rotational viscous damping, respectively |
| Fax | Pulley clamp force |
| μ | Coefficient of friction |
| μkin, μstatic | Coefficient of kinetic and static friction |
| vb, аb | Linear speed and acceleration of the belt, respectively |
| mb | Total belt mass |
| rpri, rsec | Radii of the primary and secondary pulleys, respectively |
| Φwrap | Wrap angle of belt to pulley contact point |
| Φwrap_pri, Φwrap_sec | Primary and secondary pulley wrap angles, respectively |
Power Accounting
For the power accounting, the block implements these equations.
| Bus Signal | Description | Variable | Equations | ||
|---|---|---|---|---|---|
|
|
| Engine power | Peng | |
PwrDiffrntl | Differential power | Pdiff | |||
|
| PwrBltLoss | Belt slip power loss | Pbltloss | ||
PwrGearInLoss | Input planetary gear mechanical power loss | Pgrinloss | |||
PwrGearOutLoss | Output gear reduction mechanical power loss | Pgroutloss | |||
PwrDampLoss | Mechanical damping loss | Pdamploss | |||
|
| PwrStoredTrans | Rate change in rotational kinetic energy | Pstr | ||
The equations use these variables.
| Tapp_pri, Tapp_sec | Torque applied to primary and secondary pulleys, respectively |
| Ti, To | Input and output drive shaft torque, respectively |
| Jpri, Jsec | Primary and secondary pulley rotational inertias, respectively |
| bpri, bsec | Primary and secondary pulley rotational viscous damping, respectively |
| ωpri, ωsec | Primary and secondary pulley speed, respectively |
| ωi, ωo | Input and output drive shaft speed, respectively |
| vb, аb | Linear speed and acceleration of the belt, respectively |
| rpri, rsec | Radii of the primary and secondary pulleys, respectively |
Examples
Ports
Inputs
Output
Parameters
References
[1] Ambekar, Ashok G. Mechanism and Machine Theory. New Delhi: Prentice-Hall of India, 2007.
[2] Bonsen, B. Efficiency optimization of the push-belt CVT by variator slip control. Ph.D. Thesis. Eindhoven University of Technology, 2006.
[3] CVT How Does It Work. CVT New Zealand 2010 Ltd, 10 Feb. 2011. Web. 25 Apr. 2016.
[4] Klaassen, T. W. G. L. The Empact CVT: Dynamics and Control of an Electromechanically Actuated CVT. Ph.D. Thesis. Eindhoven University of Technology, 2007.
[5] Sakagami, K. Prediction of Friction Drive Limit of Metal V-Belt. Warrendale, PA: SAE International Journal of Engines 8(3):1408-1416, 2015.
Extended Capabilities
Version History
Introduced in R2017a