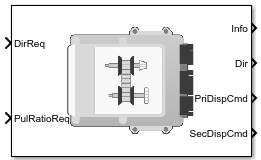
CVT Controller
Continuously variable transmission controller
Libraries:
Powertrain Blockset /
Transmission /
Transmission Controllers
Description
The CVT Controller block implements a push belt continuously variable transmission (CVT) controller. The block uses standard pulley and geometric equations to calculate the kinematic setpoints for the CVT variator. You can use the block to control a CVT.
Pulley Kinematics
Using the physical dimensions of the system, the block calculates the primary and secondary variator positions that meet the pulley ratio request.
The figure and equations summarize the geometric dependencies.
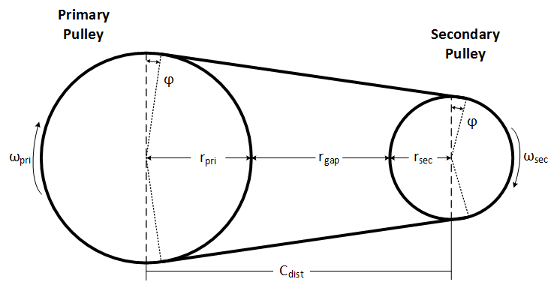
The equations use these variables.
| ratiorequest | Pulley gear ratio request |
| ratiocommand | Pulley gear ratio command, based on request and physical limitations |
| rgap | Gap distance between variator pulleys |
| Cdist | Distance between variator pulley centers |
| rpmax | Maximum variator primary pulley radius |
| rsmax | Maximum variator secondary pulley radius |
| rpmin | Minimum variator primary pulley radius |
| rsmin | Minimum variator secondary pulley radius |
| ro | Initial pulley radii with gear ratio of |
| Lo | Initial belt length, resulting from variator specification |
| xpri | Variator primary pulley displacement, resulting from controller request |
| xsec | Variator secondary pulley displacement, resulting from controller request |
| rpri | Variator primary pulley radius, resulting from controller request |
| rsec | Variator secondary pulley radius, resulting from controller request |
| Θwedge | Variator wedge angle |
| Φ | Angle of belt to pulley contact point |
| L | Belt length, resulting from variator position |
Examples
Ports
Inputs
Output
Parameters
References
[1] Ambekar, Ashok G. Mechanism and Machine Theory. New Delhi: Prentice-Hall of India, 2007.
[2] Bonsen, B. Efficiency optimization of the push-belt CVT by variator slip control. Ph.D. Thesis. Eindhoven University of Technology, 2006.
[3] CVT How Does It Work. CVT New Zealand 2010 Ltd. February 10, 2011. Accessed April 25, 2016.
[4] Klaassen, T. W. G. L. The Empact CVT: Dynamics and Control of an Electromechanically Actuated CVT. Ph.D. Thesis. Eindhoven University of Technology, 2007.
Extended Capabilities
Version History
Introduced in R2017a