La traduction de cette page n'est pas à jour. Cliquez ici pour voir la dernière version en anglais.

Examiner la 16-QAM en utilisant MATLAB

Étape 1 sur 3 dans Calculer le BER pour un système QAM avec un canal AWGN en utilisant MATLAB

Cet exemple explique comment développer un stream de données en utilisant une liaison de communications comportant un modulateur en bande de base, un canal et un démodulateur. Cet exemple représente une portion des données aléatoires dans un diagramme en tige. Les signaux émis et reçus sont illustrés dans des diagrammes de constellation, et le taux d’erreur bit (BER) est calculé. Pour ajouter un filtre de mise en forme d’impulsions à la liaison de communications, voir l’exemple Utiliser la mise en forme d’impulsion sur un signal 16-QAM. Pour ajouter un code de correction d’erreurs sans voie de retour à la liaison de communication avec un filtrage de mise en forme d'impulsion, voir l’exemple Utiliser la correction d’erreur sans voie de retour sur un signal 16-QAM.

Moduler un signal aléatoire

Le schéma de modulation utilise une bande de base 16-QAM et le signal passe au travers d’un canal à bruit blanc Gaussien additif (AWGN). Les opérations de simulation de base utilisent Communications Toolbox™ et les fonctions MATLAB® suivantes :

• rng — Contrôle la génération de nombre aléatoire

• randi — Génère un stream de données aléatoires

• bit2int — Convertit les données binaires en symboles à valeurs entières

• qammod — Module en utilisant la 16-QAM

• comm.AWGNChannel — Altère les données émises en utilisant un canal AWGN

• scatterplot — Créée des diagrammes de constellation

• qamdemod — Démodule en utilisant la 16-QAM

• int2bit — Convertit les symboles à valeurs entières en données binaires

• biterr — Calcule le BER du système

Générer un stream de données binaires aléatoires

Le format conventionnel pour représenter un signal dans MATLAB est un vecteur ou matrice. La fonction randi crée un vecteur colonne contenant les valeurs d’un stream de données binaires. La longueur du stream de données binaires (c’est-à-dire le nombre de lignes dans le vecteur colonne) est réglée arbitrairement à 30 000.

Définissez les paramètres.

M = 16;      % Modulation order (alphabet size or number of points in signal constellation)
k = log2(M); % Number of bits per symbol
n = 30000;   % Number of bits to process
sps = 1;     % Number of samples per symbol (oversampling factor)

Configurez la fonction rng sur son état par défaut, ou sur n’importe quelle valeur statique initiale, pour que l'exemple génère des résultats reproductibles. Utilisez ensuite la fonction randi pour générer des données binaires aléatoires.

rng default;
dataIn = randi([0 1],n,1); % Generate vector of binary data

Utilisez un diagramme en tige pour afficher les valeurs binaires des 40 premiers bits du stream de données binaires aléatoires. Utilisez l’opérateur deux points (:) dans l’appel de la fonction stem pour sélectionner une portion du vecteur binaire.

stem(dataIn(1:40),'filled');
title('Random Bits');
xlabel('Bit Index');
ylabel('Binary Value');

Convertir les données binaires en symboles à valeurs entières

La configuration par défaut de la fonction qammod attend des données à valeurs entières comme symboles d’entrées à moduler. Dans cet exemple, le stream de données binaires est prétraité en valeurs entières avant d’utiliser la fonction qammod. En particulier, la fonction bit2int convertit chaque quadruplet en un entier correspondant dans la plage [0, (M–1)]. L’ordre de modulation, M, est 16 dans cet exemple.

Effectuez un mapping bit-symbole en déterminant le nombre de bits par symbole définit par $$k=lo{g}_2(M)$$. Puis, utilisez la fonction bit2int pour convertir chaque quadruplet en une valeur entière.

dataSymbolsIn = bit2int(dataIn,k);

Tracez les dix premiers symboles dans un diagramme en tige.

figure;                    % Create new figure window.
stem(dataSymbolsIn(1:10));
title('Random Symbols');
xlabel('Symbol Index');
ylabel('Integer Value');

Moduler en utilisant 16-QAM

Utilisez la fonction qammod pour appliquer la modulation 16-QAM avec un offset de phase de zéro sur le vecteur colonne dataSymbolsIn, pour les mappings bit-symbole codés en binaires et Gray.

dataMod = qammod(dataSymbolsIn,M,'bin'); % Binary-encoded
dataModG = qammod(dataSymbolsIn,M);      % Gray-encoded

L’opération de modulation produit des vecteurs colonnes complexes qui contiennent des valeurs, éléments de la constellation du signal 16-QAM. Plus tard dans cet exemple, les diagrammes de constellation affichent le mapping des symboles binaires et Gray.

Pour plus d’informations sur les fonctions de modulation, veuillez consulter Digital Baseband Modulation. Pour un exemple utilisant le codage Gray avec une modulation par déplacement de phase (PSK), veuillez consulter Symbol Mapping Examples.

Ajouter de bruit blanc Gaussien

Le signal modulé passe à travers le canal en utilisant la fonction awgn avec le rapport signal à bruit spécifié (SNR). Convertissez le rapport de l'énergie par bit en fonction de la densité spectrale du bruit (${\mathit{E}}_{\mathrm{b}}/{\mathit{N}}_0$) en une valeur SNR pour une utilisation par la fonction awgn. La variable sps n’est pas significative dans cet exemple, mais permet d'étendre plus facilement l’exemple à l'utilisation de la mise en forme d’impulsion. Pour plus d’informations, voir l’exemple Utiliser la mise en forme d’impulsion sur un signal 16-QAM.

Calculez le SNR lorsque le canal a un ${\mathit{E}}_{\mathrm{b}}/{\mathit{N}}_0$ de 10 dB.

EbNo = 10;
snr = EbNo+10*log10(k)-10*log10(sps);

Passez le signal à travers le canal AWGN pour les mappings de symboles codés en binaire et Gray.

receivedSignal = awgn(dataMod,snr,'measured');
receivedSignalG = awgn(dataModG,snr,'measured');

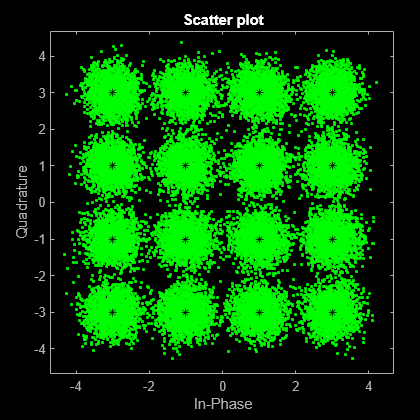
Créer un diagramme de constellation

Utilisez la fonction scatterplot pour afficher les composantes en phase et en quadratures du signal modulé, dataMod, et le signal de bruit reçu après le canal. Les effets du canal AWGN sont présents dans le diagramme de constellation.

sPlotFig = scatterplot(receivedSignal,1,0,'g.');
hold on
scatterplot(dataMod,1,0,'k*',sPlotFig)

Démoduler 16-QAM

Utilisez la fonction qamdemod pour démoduler les données reçues et obtenir en sortie des symboles à valeur entière.

dataSymbolsOut = qamdemod(receivedSignal,M,'bin'); % Binary-encoded data symbols
dataSymbolsOutG = qamdemod(receivedSignalG,M);     % Gray-coded data symbols

Convertir les symboles à valeur entière en données binaires

Utilisez la fonction int2bit pour convertir les symboles codés en binaire depuis le démodulateur QAM en vecteur binaire de longueur $\left({\mathit{N}}_{\mathrm{sym}}\times {\mathit{N}}_{\mathrm{bits}/\mathrm{sym}}\right)$. ${\mathit{N}}_{\mathrm{sym}}$ est le nombre total de symboles QAM, et ${\mathit{N}}_{\mathrm{bits}/\mathrm{sym}}$ est le nombre de bits par symbole. Pour la 16-QAM, ${\mathit{N}}_{\mathrm{bits}/\mathrm{sym}}$ = 4. Répétez le processus pour les symboles en code Gray.

Inversez le mapping bit-symbole effectué plus tôt dans cet exemple.

dataOut = int2bit(dataSymbolsOut,k);
dataOutG = int2bit(dataSymbolsOutG,k);

Calculer le BER du système

La fonction biterr calcule les statistiques d’erreur bit du stream de données binaires original, dataIn, et les streams de données reçues dataOut et dataOutG. Le codage Gray réduit le BER de manière significative.

Utilisez la fonction taux d’erreur pour calculer les statistiques d’erreurs. Utilisez la fonction fprintf pour afficher les résultats.

[numErrors,ber] = biterr(dataIn,dataOut);
fprintf('\nThe binary coding bit error rate is %5.2e, based on %d errors.\n', ...
    ber,numErrors)

The binary coding bit error rate is 2.27e-03, based on 68 errors.

[numErrorsG,berG] = biterr(dataIn,dataOutG);
fprintf('\nThe Gray coding bit error rate is %5.2e, based on %d errors.\n', ...
    berG,numErrorsG)

The Gray coding bit error rate is 1.63e-03, based on 49 errors.

Tracer les constellations de signaux

Le diagramme de constellation présenté précédemment traçait les points de la constellation QAM, mais n’indiquait pas le mapping entre les valeurs des symboles et les points de constellation. Dans cette section, le diagramme de constellation indique les mappings pour les codages de données en binaire et Gray aux points de constellation.

Montrer le mapping des symboles binaires codés Gray et naturels pour les constellations 16-QAM

Appliquer la modulation 16-QAM pour réaliser des ensembles de points de constellation en utilisant le mapping de symboles codés en binaire et le mapping de symboles codés Gray.

M = 16;                       % Modulation order
x = (0:15);                   % Integer input
symbin = qammod(x,M,'bin');   % 16-QAM output (binary-coded)
symgray = qammod(x,M,'gray'); % 16-QAM output (Gray-coded)

Utilisez la fonction scatterplot pour tracer le diagramme de constellation et l’annoter avec des représentations binaires (rouge) et Gray (noir) des points de constellation.

scatterplot(symgray,1,0,'b*');
for k = 1:M
    text(real(symgray(k)) - 0.0,imag(symgray(k)) + 0.3, ...
        dec2base(x(k),2,4));
     text(real(symgray(k)) - 0.5,imag(symgray(k)) + 0.3, ...
         num2str(x(k)));
    
    text(real(symbin(k)) - 0.0,imag(symbin(k)) - 0.3, ...
        dec2base(x(k),2,4),'Color',[1 0 0]);
    text(real(symbin(k)) - 0.5,imag(symbin(k)) - 0.3, ...
        num2str(x(k)),'Color',[1 0 0]);
end
title('16-QAM Symbol Mapping')
axis([-4 4 -4 4])

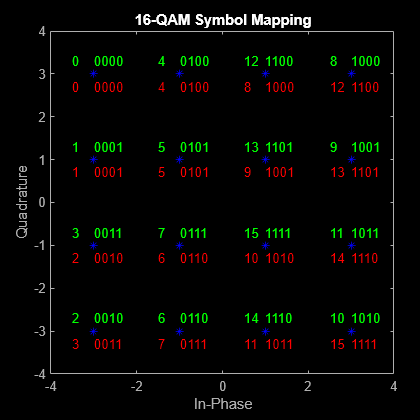
Examiner les tracés

L’utilisation du mapping des symboles codés Gray améliore les performances du BER, car les points de la constellation du signal codé Gray ne diffèrent de chaque point voisin adjacent que d’un bit. Tandis qu’avec le mapping de symboles codés en binaire, certains points adjacents de la constellation diffèrent les uns des autres de deux bits. Par exemple, les valeurs codées en binaire pour 1 (0 0 0 1) et 2 (0 0 1 0) diffèrent de 2 bits (le troisième et quatrième bit).

Sujets associés

• Calculer le BER pour un système QAM avec un canal AWGN en utilisant MATLAB

Calculer le BER pour un système QAM avec un canal AWGN en utilisant MATLAB

Suivant