AGC
Adaptively adjust gain for constant signal-level output
Libraries:
Communications Toolbox /
RF Impairments Correction
Description
The automatic gain controller (AGC) block adaptively adjusts its gain to achieve a constant signal level at the output.
This icon shows the AGC block with the optional Px port.![]()
Examples
The doc_agc_received_signal_amplitude model uses an AGC block to adjust the received signal power to approximately 1 watt.
A constellation diagram displays the signal before and after the signal level is adjusted by the AGC block. Random integer-valued symbols are QPSK modulated and then the signal level is scaled down by using a Gain block. The AGC block adjusts the signal to achieve a desired power level of 1 W. A constellation diagram displays the signal input to and output from the AGC block.
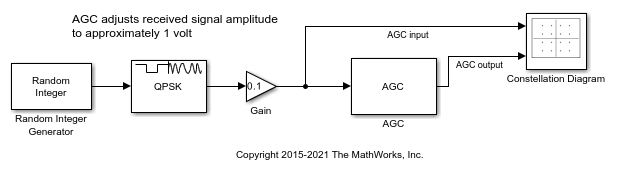
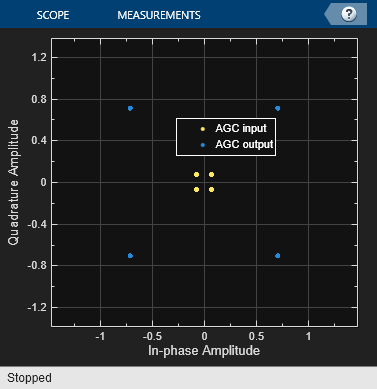
Run the model and display the constellation diagram to show the signal level adjustments performed by the AGC block.
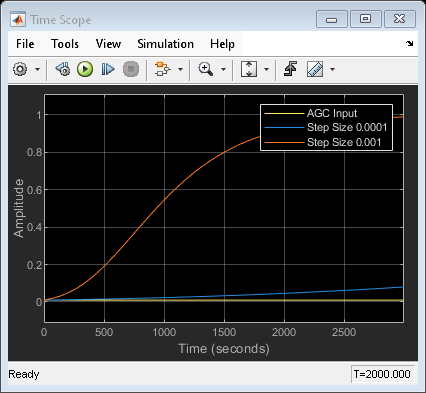
This model uses AGC blocks with different step size settings to adjust the received signal power.
A time scope plots the effect of step size on AGC performance. Random integer-valued symbols are QPSK modulated and then the signal level is scaled down by using a Gain block. Three signal branches flow to a time scope to plot the received signal magnitude with no AGC, AGC with step size set to 0.0001, and AGC with step size set to 0.001.

Run the model and display the time scope to show the signal level adjustments performed by the AGC blocks.
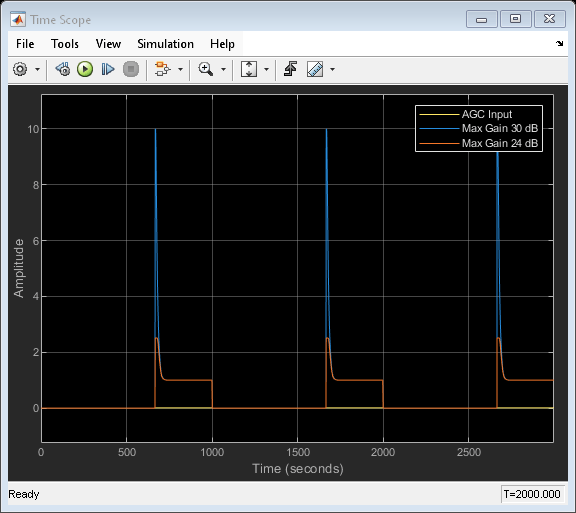
This model uses AGC blocks with different maximum gain settings to adjust the received signal power.
A time scope plots the effect of maximum gain on AGC performance. The maximum gain setting affects the ability of the AGC to reach its target output power. Random integer-valued symbols are QPSK modulated and then the signal level is scaled down by using a Gain block. Three signal branches flow to a time scope to plot the received signal magnitude with no AGC, AGC with maximum gain set to 30 dB, and AGC with maximum gain set to 24 dB.
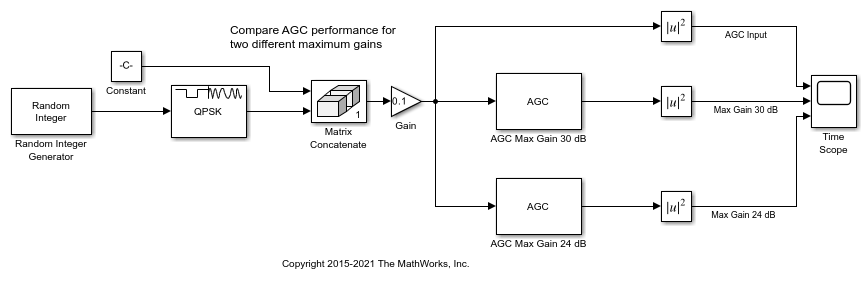
Run the model and display the time scope to show the signal level adjustments performed by the AGC blocks.
Ports
Input
Input signal, specified as a column vector. This port is unnamed on the block mask.
Data Types: single | double | int | uint
Complex Number Support: Yes
Output
Output signal, returned as an NS-element column vector. NS is the length of the input signal. The output signal is the same data type as the input signal.
Power level estimate, returned as an
NS-element column vector.
NS is the length of the
input signal. You can use powerlevel as an energy
detector output.
Dependencies
To enable this port, select the Enable output of estimated input power parameter.
Parameters
To edit block parameters interactively, use the Property Inspector. From the Simulink® Toolstrip, on the Simulation tab, in the Prepare gallery, select Property Inspector.
Step size for gain updates, specified as a positive scalar. Increasing the step size enables the AGC to respond more quickly to changes in the input signal level but increases variation in the output signal level after reaching steady-state operation. For more information, see AGC Performance Criteria.
Target output power level, specified as a positive scalar. The power level is measured in watts referenced to 1 ohm.
Length of the averaging window in samples, specified as a positive integer. For more information on how the averaging length influences the variance of the AGC output signal in steady-state operation and the execution speed, see Tips.
Maximum power gain in dB, specified as a positive scalar. Large gain adjustments can cause clipping when a small input signal power suddenly increases. Use this property to avoid large gain adjustments by limiting the gain that the AGC applies to the input signal. For an example, see Compare AGC Performance for Different Maximum Gains.
Select this check box to provide an output port, Px,
that returns an estimate of the input signal power.
Type of simulation to run, specified as Interpreted
execution or Code generation.
Interpreted execution— Simulate the model by using the MATLAB® interpreter. This option requires less startup time, but the speed of subsequent simulations is slower than with theCode generationoption. In this mode, you can debug the source code of the block.Code generation— Simulate the model by using generated C code. The first time you run a simulation, Simulink generates C code for the block. The model reuses the C code for subsequent simulations unless the model changes. This option requires additional startup time, but the speed of the subsequent simulations is faster than with theInterpreted executionoption.
For more information, see Interpreted Execution vs. Code Generation (Simulink).
Block Characteristics
Data Types |
|
Multidimensional Signals |
|
Variable-Size Signals |
|
More About
The AGC implementation uses a logarithmic feedback loop. As this figure of the logarithmic-loop AGC algorithm shows, the output signal is the product of the input signal and the exponential of the loop gain. The error signal is the difference between the reference level and the product of the logarithm of the detector output and the exponential of the loop gain. After multiplying by the step size, the AGC passes the error signal to an integrator.

The logarithmic-loop AGC performs well for a variety of signal types, including amplitude modulation. The AGC Detector is applied to the input signal, which improves convergence times, but increases signal power variation at the detector input. Large signal variation at the detector input is acceptable for floating-point systems.
Mathematically, the algorithm is summarized as
where:
x is the input signal.
y is the output signal.
g is the loop gain.
Detector(•) is the detector function.
z is the detector output.
A is the reference value.
err is the error signal.
K is the step size.
The AGC detector output, z, computes a square law detector given by
where N is the update period. The square law detector produces an output proportional to the square of the input signal y.
Increasing the step size decreases the attack time and decay times, but it also increases gain pumping.
Attack time — The duration taken for the AGC to respond to an increase in the input amplitude
Decay time — The duration taken for the AGC to respond to a decrease in the input amplitude
Gain pumping — The variation in the gain value during steady-state operation
Tips
This block is designed for streaming applications.
If the signal amplitude does not change within the frame, you can simulate an ideal AGC by calculating the average gain desired for a frame of samples. Then, apply the gain to each sample in the frame.
If you use the AGC with higher order QAM signals, you might need to reduce the variation in the gain during steady-state operation. Inspect the constellation diagram at the output of the AGC during steady-state operation. You can increase the averaging length to avoid frequent gain adjustments. An increase in averaging length reduces execution speed.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.
Version History
Introduced in R2013a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Sélectionner un site web
Choisissez un site web pour accéder au contenu traduit dans votre langue (lorsqu'il est disponible) et voir les événements et les offres locales. D’après votre position, nous vous recommandons de sélectionner la région suivante : .
Vous pouvez également sélectionner un site web dans la liste suivante :
Comment optimiser les performances du site
Pour optimiser les performances du site, sélectionnez la région Chine (en chinois ou en anglais). Les sites de MathWorks pour les autres pays ne sont pas optimisés pour les visites provenant de votre région.
Amériques
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)