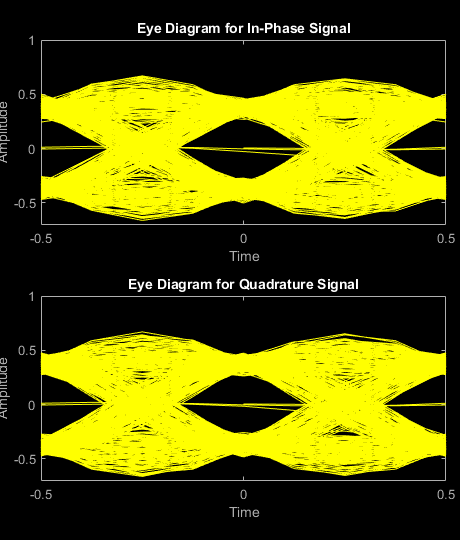
eyediagram
Generate eye diagram
Syntax
Description
eyediagram(
specifies plot attributes for the eye diagram.x,n,period,offset,plotstring)
h = eyediagram(___)
Examples
Input Arguments
Output Arguments
Version History
Introduced before R2006a