Prepare Data for CSI Processing

Since R2025a

This example shows how to generate channel estimates and prepare a data set to train AI-based systems, such as an autoencoder for channel state information (CSI) feedback compression. In this example, you:

1. Generate channel estimates.

2. Preprocess the channel estimates.

3. Visualize the preprocessed channel estimate.

4. Generate a data set of channel estimates in bulk for training neural networks.

Introduction

In conventional 5G radio networks, CSI parameters are quantities that relate to the state of a channel and are extracted from the channel estimate array. The CSI feedback includes several parameters, such as the channel quality indication (CQI), the precoding matrix indices (PMI) with different codebook sets, and the rank indicator (RI). The user equipment (UE) uses the CSI reference signal (CSI-RS) to measure and compute the CSI parameters. The UE reports CSI parameters to the access network node (gNB) as feedback. Upon receiving the CSI parameters, the gNB schedules downlink data transmissions with attributes such as modulation scheme, code rate, number of transmission layers, and MIMO precoding. This figure shows an overview of a CSI-RS transmission, CSI feedback, and the transmission of downlink data that is scheduled based on the CSI parameters.

The UE processes the channel estimate to reduce the amount of CSI feedback data. As an alternative approach, the UE compresses and sends back the channel estimate array. After reception, the gNB decompresses and processes the channel estimate to determine downlink data parameters. You can compress and decompress the CSI feedback using an autoencoder neural network [2, 3]. This approach eliminates the use of the existing quantized codebook and can improve overall system performance. For more information, see NR PDSCH Throughput Using Channel State Information Feedback (5G Toolbox).

Generate and Preprocess Data

The first step of designing an AI-based system is to prepare training and testing data. In this example, you generate simulated channel estimates and preprocess the data. Use 5G Toolbox™ functions to configure a channel with the following parameters.

Carrier Configuration

Set the number of resource blocks to 52 and subcarrier spacing to 15.

nSizeGrid = 52;                                   % Number resource blocks (RB)
                                                  % 12 subcarriers per RB
options.SubcarrierSpacing = 15; % 15, 30, 60, 120 kHz

Create an nrCarrierConfig object and set the carrier parameters.

carrier = nrCarrierConfig;
carrier.NSizeGrid = nSizeGrid;
carrier.SubcarrierSpacing = options.SubcarrierSpacing;
waveInfo = nrOFDMInfo(carrier);

Configure MIMO Channel

Specify the transmit antenna size and receive antenna size.

options.TxAntennaSize = [2 2 2 1 1];   % rows, columns, polarization, panels
options.RxAntennaSize = [2 1 1 1 1];   % rows, columns, polarization, panels
options.MaxDoppler = 5;                % Hz
options.RMSDelaySpread = 300e-9;       % s
numSubCarriers = carrier.NSizeGrid*12; % 12 subcarriers per RB

Select a delay profile to represent the multiple-input multiple-output (MIMO) fading channel.

options.DelayProfile = "CDL-C"; % CDL-A, CDL-B, CDL-C, CDL-D, CDL-D, CDL-E

Create an nrCDLChannel object and set the channel parameters.

samplesPerSlot = ...
  sum(waveInfo.SymbolLengths(1:waveInfo.SymbolsPerSlot));

channel = nrCDLChannel;
channel.DelayProfile = options.DelayProfile;
channel.DelaySpread = options.RMSDelaySpread;     % s
channel.MaximumDopplerShift = options.MaxDoppler; % Hz
channel.RandomStream = "Global stream";
channel.TransmitAntennaArray.Size = options.TxAntennaSize;
channel.ReceiveAntennaArray.Size = options.RxAntennaSize;
channel.ChannelFiltering = false;        % No filtering for 
                                         % perfect estimate
channel.NumTimeSamples = samplesPerSlot; % 1 slot worth of samples
channel.SampleRate = waveInfo.SampleRate;

Simulate Channel

Simulate the channel to get the perfect channel estimate Hest. The nrPerfectChannelEstimate function performs perfect channel estimation. The function first reconstructs the channel impulse response from the channel path gains pathGains and the path filter impulse response pathFilters. The function then performs orthogonal frequency division multiplexing (OFDM) demodulation. The carrier variable specifies the parameters for the OFDM demodulation.

[pathGains,sampleTimes] = channel();
pathFilters = getPathFilters(channel);

Set ZeroTimingOffset option to true, to get the channel estimate with true timing delay. This setting ensures continuous channel estimates. Set ZeroTimingOffset option to false, to get the estimated timing delay based on the strongest channel path.

options.ZeroTimingOffset = true;
if options.ZeroTimingOffset
  % Perfect timing sync
  offset = 0;
else
  offset = nrPerfectTimingEstimate(pathGains, pathFilters);
end
Hest = nrPerfectChannelEstimate(carrier, pathGains, ...
                                pathFilters, offset, ...
                                sampleTimes);
reset(channel);

The channel estimate matrix is an ${\left[{\mathit{N}}_{\mathrm{subcarriers}}{\mathit{N}}_{\mathrm{symbols}}{\mathit{N}}_{\mathrm{rx}}{\mathit{N}}_{\mathrm{tx}}\right]}_{}$array for each slot.

% Get dimensions of Channel estimate
[nSub,nS,nRx,nTx] = size(Hest)

nSub = 
624

nS = 
14

nRx = 
2

nTx = 
8

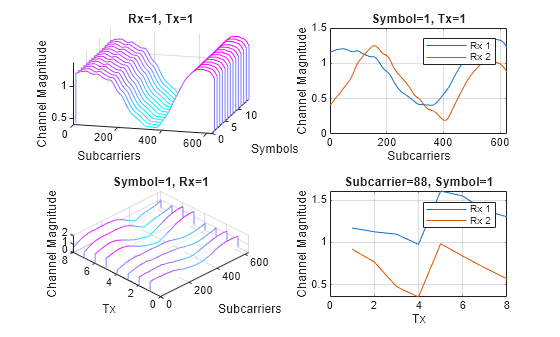
Plot the channel response. The upper left plot shows the channel frequency response as a function of time (symbols) for receive antenna 1 and transmit antenna 1. The lower left plot shows the channel frequency response as a function of transmit antennas for symbol 1 and receive antenna 1. The upper right plot shows the channel frequency response for all receive antennas for symbol 1 and transmit antenna 1. The lower right plot shows the change in channel magnitude response as a function of transmit antennas for all receive antennas for a subcarrier and symbol 1.

helperPlotChannelResponse(Hest)

Preprocess Channel Estimate

You can preprocess the channel estimate to reduce the size using these methods,

• Delay-angle domain: Real-valued array collected post truncation.

• Frequency-spatial domain: Real-valued array collected after 2-D inverse discrete Fourier transform (IDFT).

This figure shows preprocessing of the channel estimate reduction.

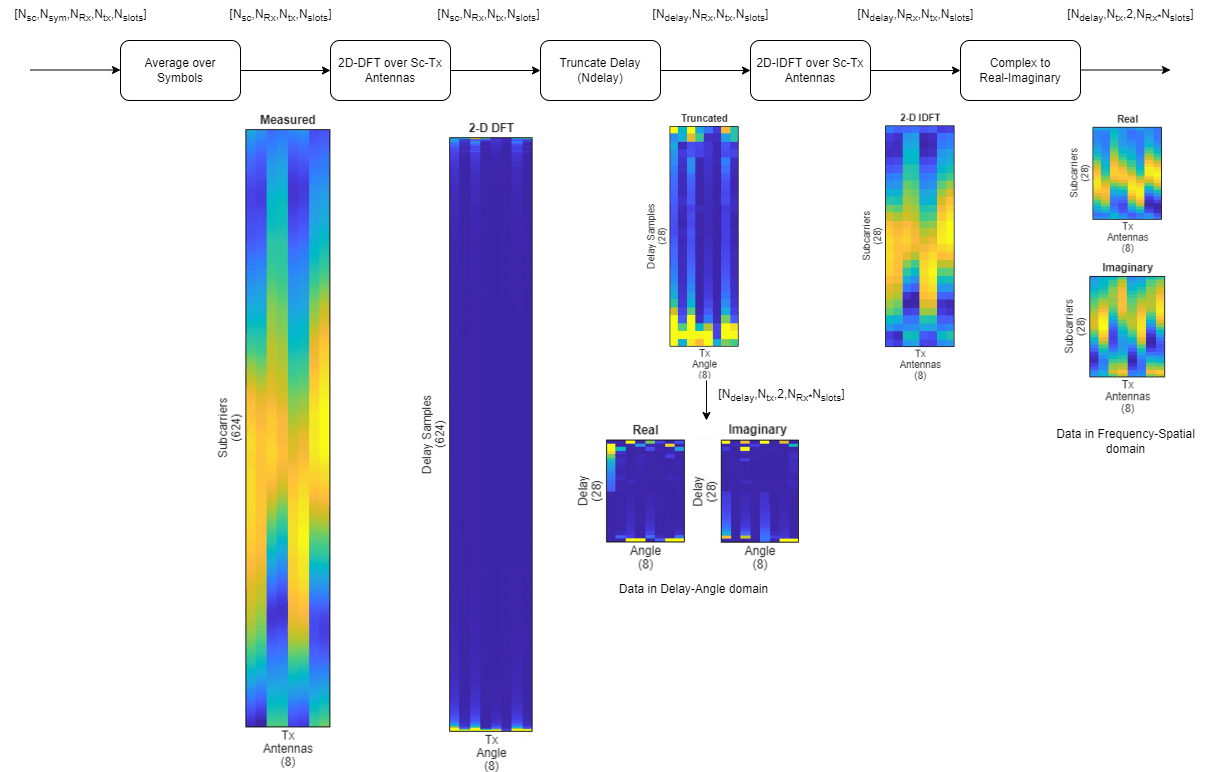
Assume that the channel coherence time is much larger than the slot time. Average the channel estimate over a slot and obtain a $\left[{\mathit{N}}_{\mathrm{subcarriers}}1{\mathit{N}}_{\mathrm{rx}}{\mathit{N}}_{\mathrm{tx}}\right]$array.

Hmean = squeeze(mean(Hest,2));

To enable operation on subcarriers and Tx antennas, move the Tx and Rx antenna dimensions to the second and third dimensions, respectively.

Hmean = permute(Hmean,[1 3 2]);

To obtain the delay-angle representation of the channel, apply a 2-D discrete Fourier transform (DFT) over subcarriers and Tx antennas for each Rx antenna and slot.

Hdft2 = fft2(Hmean);

Since the multipath delay in the channel is limited, truncate the delay dimension to remove values that do not carry information. The sampling period on the delay dimension is ${\mathit{T}}_{\mathrm{delay}}=1/({\mathit{N}}_{\mathrm{subcarriers}}\ast {\mathit{F}}_{\mathrm{ss}})$, where ${\mathit{F}}_{\mathrm{ss}}$ is subcarrier spacing. The expected RMS delay spread in delay samples is ${\tau }_{\mathrm{RMS}}/{\mathit{T}}_{\mathrm{delay}}$, where ${\tau }_{\mathrm{RMS}}$ is the RMS delay spread of the channel in seconds.

Tdelay = 1/(numSubCarriers*carrier.SubcarrierSpacing*1e3);
rmsTauSamples = channel.DelaySpread/Tdelay;
maxTruncationFactor = floor(numSubCarriers/rmsTauSamples);

Truncate the channel estimate to an even number of samples that is 10 times the expected RMS delay spread. Increasing the truncationFactor value decreases performance loss due to preprocessing, but it increases the neural network complexity, the number of required training data points, and the training time. A neural network with more learnable parameters might not converge to a better solution.

options.TruncationFactor = 10;
options.MaxDelay = round((channel.DelaySpread/Tdelay)*options.TruncationFactor/2)*2

options = struct with fields:
    SubcarrierSpacing: 15
        TxAntennaSize: [2 2 2 1 1]
        RxAntennaSize: [2 1 1 1 1]
           MaxDoppler: 5
       RMSDelaySpread: 3.0000e-07
         DelayProfile: "CDL-C"
     ZeroTimingOffset: 1
     TruncationFactor: 10
             MaxDelay: 28

Calculate the truncation indices and truncate the channel estimate.

midPoint = floor(nSub/2);
lowerEdge = midPoint - (nSub-options.MaxDelay)/2 + 1;
upperEdge = midPoint + (nSub-options.MaxDelay)/2;
Htemp = Hdft2([1:lowerEdge-1 upperEdge+1:end],:,:);

Select the domain for preprocessed data preparation in delay-angle domain or frequency-spatial domain.

options.DataDomain = "Frequency-Spatial";
switch options.DataDomain
    case "Delay-Angle"
        Htrunc = Htemp;
    case "Frequency-Spatial"
        Htrunc = ifft2(Htemp);
end
HtruncReal = cat(3, real(Htrunc), imag(Htrunc));
size(HtruncReal)

ans = 1×3

    28     8     4

Visualize Generated Data

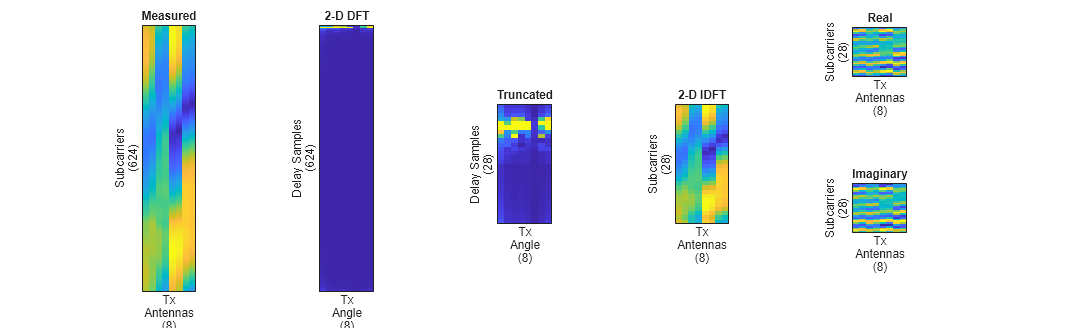
Plot the channel estimate signal at each stage of the preprocessing.

helperPlotCSIFeedbackPreprocessingSteps(Hmean(:,:,1), ...
                                        Hdft2(:,:,1), Htemp(:,:,1), ...
                                        Htrunc(:,:,1), nSub, ...
                                        nTx, ...
                                        options.MaxDelay, ...
                                        options.DataDomain);

Prepare Data in Bulk

You can set the number of samples to be generated for the data set below. For a shorter run time, the number of samples is set to 500.

numSamples = 500;

If Parallel Computing Toolbox™ is available, set the autoEncOpt.UseParallel variable to true to enable parallel data generation. Data generation takes about six minute for 15000 samples on a PC with Intel® Xeon® W-2133 CPU @ 3.60 GHz while running in parallel on six workers.

options.UseParallel = false;

Set the options.SaveData variable to true, to save the preprocessed channel estimates to .mat files.

options.SaveData = true;
options.DataDir = "Data";
options.DataFilePrefix = "CH_est";

Generate Samples

The helperCSINetGenerateData helper function generates 'numSamples' of preprocessed $\left[{\mathit{N}}_{\mathrm{delay}}{\mathit{N}}_{\mathrm{tx}}2\right]$ channel estimates by using the process described. When you enable options.SaveData, the function saves each $\left[{\mathit{N}}_{\mathrm{delay}}{\mathit{N}}_{\mathrm{tx}}2{\mathit{N}}_{\mathrm{rx}}\right]$ channel estimate as an individual file in the options.DataDir with the prefix of options.DataFilePrefix. The function also returns the generated data in HtruncReal.

HtruncReal = helperCSINetGenerateData(numSamples,channel,carrier,options);

Starting CSI data generation
1 worker(s) running
00:00:07 - 20% Completed
00:00:21 - 60% Completed
00:00:33 - 100% Completed

The HtruncReal variable contains $$N_{frames}$$ of frames. Each frame has data for $$N_{rx}$$ receive antennas, which are independent.

[maxDelay,nTx,Niq,nRx,Nframes] = size(HtruncReal)

maxDelay = 
28

nTx = 
8

Niq = 
2

nRx = 
2

Nframes = 
250

Combine frames and antennas.

HtruncReal = reshape(HtruncReal,maxDelay,nTx,Niq,nRx*Nframes);
[maxDelay,nTx,Niq,Nsamples] = size(HtruncReal)

maxDelay = 
28

nTx = 
8

Niq = 
2

Nsamples = 
500

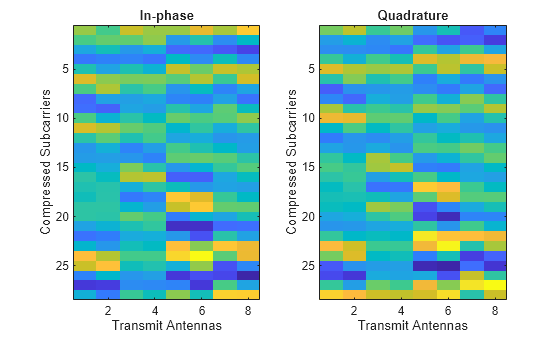
Display a sample.

figure
subplot(1,2,1)
imagesc(HtruncReal(:,:,1,1,1))
xlabel("Transmit Antennas")
ylabel("Compressed Subcarriers")
title("In-phase")
subplot(1,2,2)
imagesc(HtruncReal(:,:,2,1,1))
xlabel("Transmit Antennas")
ylabel("Compressed Subcarriers")
title("Quadrature")

Further Exploration

This example shows how to generate and preprocess data for different autoencoder based CSI Feedback compression. For information on how to design and train autoencoder CSI Feedback networks, see these examples:

• CSI Feedback with Autoencoders (5G Toolbox)

• CSI Feedback with Transformer Autoencoder

• Train PyTorch Channel Prediction Models

• Offline Training and Testing of PyTorch Model for CSI Feedback Compression

• Online Training and Testing of PyTorch Model for CSI Feedback Compression

• CSINet Channel Compression in MATLAB Using Keras

Helper Functions

• helperCSIGenerateData.m

• helperCSINetGenerateData.m

• helperCSIChannelEstimate.m

• helperCSIPreprocessChannelEstimate.m

• helperValidateCSIDataFiles.m

Local Functions

function helperPlotChannelResponse(Hest)
% helperPlotChannelResponse Plot channel response

figure
tiledlayout(2,2)
nexttile
waterfall(abs(Hest(:,:,1,1))')
xlabel("Subcarriers");
ylabel("Symbols");
zlabel("Channel Magnitude")
view(15,30)
colormap("cool")
title("Rx=1, Tx=1")
nexttile
plot(squeeze(abs(Hest(:,1,:,1))))
grid on
xlabel("Subcarriers");
ylabel("Channel Magnitude")
legend("Rx 1", "Rx 2")
title("Symbol=1, Tx=1")
nexttile
waterfall(squeeze(abs(Hest(:,1,1,:)))')
view(-45,75)
grid on
xlabel("Subcarriers");
ylabel("Tx");
zlabel("Channel Magnitude")
title("Symbol=1, Rx=1")
nexttile
nSubCarriers = size(Hest,1);
subCarrier = randi(nSubCarriers);
plot(squeeze(abs(Hest(subCarrier,1,:,:)))') 
grid on
xlabel("Tx");
ylabel("Channel Magnitude")
legend("Rx 1", "Rx 2")
title("Subcarrier=" + subCarrier + ", Symbol=1")
end

function helperPlotCSIFeedbackPreprocessingSteps(Hmean,Hdft2,Htemp,Htrunc, ...
    nSub,nTx,maxDelay,dataDomain)
% helperPlotCSIFeedbackPreprocessingSteps Plot preprocessing workflow

hfig = figure;
hfig.Position(3) = hfig.Position(3)*2;
subplot(2,5,[1 6])
himg = imagesc(abs(Hmean));
himg.Parent.YDir = "normal";
himg.Parent.Position(3) = 0.05;
himg.Parent.XTick=''; himg.Parent.YTick='';
xlabel(sprintf('Tx\nAntennas\n(%d)',nTx));
ylabel(sprintf('Subcarriers\n(%d)',nSub'));
title("Measured")
subplot(2,5,[2 7])
himg = image(abs(Hdft2));
himg.Parent.YDir = "normal";
himg.Parent.Position(3) = 0.05;
himg.Parent.XTick=''; himg.Parent.YTick='';
title("2-D DFT")
xlabel(sprintf('Tx\nAngle\n(%d)',nTx));
ylabel(sprintf('Delay Samples\n(%d)',nSub'));
subplot(2,5,[3 8])
himg = image(abs(Htemp));
himg.Parent.YDir = "normal";
himg.Parent.Position(3) = 0.05;
himg.Parent.Position(4) = himg.Parent.Position(4)*10*maxDelay/nSub;
himg.Parent.Position(2) = (1 - himg.Parent.Position(4)) / 2;
himg.Parent.XTick=''; himg.Parent.YTick='';
xlabel(sprintf('Tx\nAngle\n(%d)',nTx));
ylabel(sprintf('Delay Samples\n(%d)',maxDelay'));
title("Truncated")
if strcmpi(dataDomain,"Frequency-Spatial")
    subplot(2,5,[4 9])
    himg = imagesc(abs(Htrunc));
    himg.Parent.YDir = "normal";
    himg.Parent.Position(3) = 0.05;
    himg.Parent.Position(4) = himg.Parent.Position(4)*10*maxDelay/nSub;
    himg.Parent.Position(2) = (1 - himg.Parent.Position(4)) / 2;
    himg.Parent.XTick=''; himg.Parent.YTick='';
    xlabel(sprintf('Tx\nAntennas\n(%d)',nTx));
    ylabel(sprintf('Subcarriers\n(%d)',maxDelay'));
    title("2-D IDFT")
    subplot(2,5,5)
    himg = imagesc(real(Htrunc));
    himg.Parent.YDir = "normal";
    himg.Parent.Position(3) = 0.05;
    himg.Parent.Position(4) = himg.Parent.Position(4)*10*maxDelay/nSub;
    himg.Parent.Position(2) = himg.Parent.Position(2) + 0.18;
    himg.Parent.XTick=''; himg.Parent.YTick='';
    xlabel(sprintf('Tx\nAntennas\n(%d)',nTx));
    ylabel(sprintf('Subcarriers\n(%d)',maxDelay'));
    title("Real")
    subplot(2,5,10)
    himg = imagesc(imag(Htrunc));
    himg.Parent.YDir = "normal";
    himg.Parent.Position(3) = 0.05;
    himg.Parent.Position(4) = himg.Parent.Position(4)*10*maxDelay/nSub;
    himg.Parent.Position(2) = himg.Parent.Position(2) + 0.18;
    himg.Parent.XTick=''; himg.Parent.YTick='';
    xlabel(sprintf('Tx\nAntennas\n(%d)',nTx));
    ylabel(sprintf('Subcarriers\n(%d)',maxDelay'));
    title("Imaginary")
elseif strcmpi(dataDomain,"Delay-Angle")
    subplot(2,5,4)
    himg = image(real(Htrunc));
    himg.Parent.YDir = "normal";
    himg.Parent.Position(3) = 0.05;
    himg.Parent.Position(4) = himg.Parent.Position(4)*10*maxDelay/nSub;
    himg.Parent.Position(2) = himg.Parent.Position(2) + 0.18;
    himg.Parent.XTick=''; himg.Parent.YTick='';
    xlabel(sprintf('Angle\n(%d)',nTx));
    ylabel(sprintf('Delay\n(%d)',maxDelay'));
    title("Real")
    subplot(2,5,9)
    himg = image(imag(Htrunc));
    himg.Parent.YDir = "normal";
    himg.Parent.Position(3) = 0.05;
    himg.Parent.Position(4) = himg.Parent.Position(4)*10*maxDelay/nSub;
    himg.Parent.Position(2) = himg.Parent.Position(2) + 0.18;
    himg.Parent.XTick=''; himg.Parent.YTick='';
    xlabel(sprintf('Angle\n(%d)',nTx));
    ylabel(sprintf('Delay\n(%d)',maxDelay'));
    title("Imaginary")
end
end

References

[1] 3GPP TR 38.901. "Study on channel model for frequencies from 0.5 to 100 GHz." 3rd Generation Partnership Project; Technical Specification Group Radio Access Network.

[2] Wen, Chao-Kai, Wan-Ting Shih, and Shi Jin. "Deep Learning for Massive MIMO CSI Feedback." IEEE Wireless Communications Letters 7, no. 5 (October 2018): 748–51. https://doi.org/10.1109/LWC.2018.2818160.

[3] Zimaglia, Elisa, Daniel G. Riviello, Roberto Garello, and Roberto Fantini. "A Novel Deep Learning Approach to CSI Feedback Reporting for NR 5G Cellular Systems." In 2020 IEEE Microwave Theory and Techniques in Wireless Communications (MTTW), 47–52. Riga, Latvia: IEEE, 2020. https://doi.org/10.1109/MTTW51045.2020.9245055.