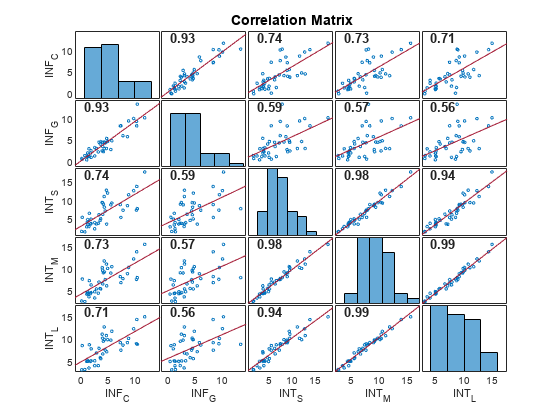
corrplot
Plot variable correlations
Syntax
Description
[ plots Pearson's correlation coefficients
between all pairs of variables in the input matrix of time series data. The plot is a
R,PValue]
= corrplot(X)numVars-by-numVars grid, where
numVars is the number of time series variables (columns) in the data,
including the following subplots:
Each off diagonal subplot contains a scatterplot of a pair of variables with a least-squares reference line, the slope of which is equal to the displayed correlation coefficient.
Each diagonal subplot contains the distribution of a variable as a histogram.
Also, the function returns the correlation matrix in the plots and a matrix of p-values for testing the null hypothesis that each pair of coefficients is not correlated against the alternative hypothesis of a nonzero correlation.
[
plots the Pearson's correlation coefficients between all pairs of variables in the input
table or timetable, and also returns tables for the correlation matrix and matrix of
p-values.R,PValue] = corrplot(Tbl)
To select a subset of variables, for which to plot the correlation matrix, use the
DataVariables name-value argument.
[___] = corrplot(___,
specifies options using one or more name-value arguments in
addition to any of the input argument combinations in previous syntaxes.
Name=Value)corrplot returns the output argument combination for the
corresponding input arguments. For example,
corrplot(Tbl,Type="Spearman",TestR="on",DataVariables=1:5) computes
Spearman’s rank correlation coefficient for the first 5 variables of the table
Tbl and tests for significant correlation coefficients.
corrplot(___) plots the correlation matrix.
corrplot(
plots on the axes specified by ax,___)ax instead of
the current axes (gca). ax can precede any of the input
argument combinations in the previous syntaxes.
[___, plots the diagnostics of the input series and
additionally returns handles to plotted graphics objects. Use elements of
H]
= corrplot(___)H to modify properties of the plot after you create it.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
Tips
The setting
Rows="pairwise"(the default) can return a correlation matrix that is not positive definite. The settingRows="complete"returns a positive-definite matrix, but, in general, the estimates are based on fewer observations.
Algorithms
corrplotcomputes p-values for Pearson’s correlation by transforming the correlation to create a t-statistic withnumObs– 2 degrees of freedom. The transformation is exact when the input time series data is normal.corrplotcomputes p-values for Kendall’s and Spearman’s rank correlations by using either the exact permutation distributions (for small sample sizes) or large-sample approximations.corrplotcomputes p-values for two-tailed tests by doubling the more significant of the two one-tailed p-values.