Performance Considerations
Managing Memory
There are two general approaches for managing memory when solving most problems supported by the SDE engine:
Managing Memory with Outputs
Perform a traditional simulation to simulate the underlying variables of interest, specifically requesting and then manipulating the output arrays.
This approach is straightforward and the best choice for small or medium-sized problems. Since its outputs are arrays, it is convenient to manipulate simulated results in the MATLAB® matrix-based language. However, as the scale of the problem increases, the benefit of this approach decreases, because the output arrays must store large quantities of possibly extraneous information.
For example, consider pricing a European option in which the terminal price of
the underlying asset is the only value of interest. To ease the memory burden of
the traditional approach, reduce the number of simulated periods specified by
the required input NPeriods and specify the optional input
NSteps. This enables you to manage memory without
sacrificing accuracy (see Optimizing Accuracy: About Solution Precision and Error).
In addition, simulation methods can determine the number of output arguments and allocate memory accordingly. Specifically, all simulation methods support the same output argument list:
[Paths,Times,Z]
where Paths and Z can be large,
three-dimensional time series arrays. However, the underlying noise array is
typically unnecessary, and is only stored if requested as an output. In other
words, Z is stored only at your request; do not request it if
you do not need it.
If you need the output noise array Z, but do not need the
Paths time series array, then you can avoid storing
Paths two ways:
It is best practice to use the
~output argument placeholder. For example, use the following output argument list to storeZandTimes, but notPaths:[~,Times,Z]
Use the optional input flag
StorePaths, which all simulation methods support. By default,Pathsis stored (StorePaths=true). However, settingStorePathstofalsereturnsPathsas an empty matrix.
Managing Memory Using End-of-Period Processing Functions
Specify one or more end-of-period processing functions to manage and store only the information of interest, avoiding simulation outputs altogether.
This approach requires you to specify one or more end-of-period processing
functions, and is often the preferred approach for large-scale problems. This
approach allows you to avoid simulation outputs altogether. Since no outputs are
requested, the three-dimensional time series arrays Paths and
Z are not stored.
This approach often requires more effort, but is far more elegant and allows you to customize tasks and dramatically reduce memory usage. See Price European Stock Options Using Monte Carlo Simulation.
Enhancing Performance
The following approaches improve performance when solving SDE problems:
Specifying model parameters as traditional MATLAB arrays and functions, in various combinations. This provides a flexible interface that can support virtually any general nonlinear relationship. However, while functions offer a convenient and elegant solution for many problems, simulations typically run faster when you specify parameters as double-precision vectors or matrices. Thus, it is a good practice to specify model parameters as arrays when possible.
Use models that have overloaded Euler simulation methods, when possible. Using Brownian motion (
BM) and geometric Brownian motion (GBM) models that provide overloaded Euler simulation methods take advantage of separable, constant-parameter models. These specialized methods are exceptionally fast, but are only available to models with constant parameters that are simulated without specifying end-of-period processing and noise generation functions.Replace the simulation of a constant-parameter, univariate model derived from the
SDEDDOclass with that of a diagonal multivariate model. Treat the multivariate model as a portfolio of univariate models. This increases the dimensionality of the model and enhances performance by decreasing the effective number of simulation trials.Note
This technique is applicable only to constant-parameter univariate models without specifying end-of-period processing and noise generation functions.
Take advantage of the fact that simulation methods are designed to detect the presence of
NaN(not a number) conditions returned from end-of-period processing functions. ANaNrepresents the result of an undefined numerical calculation, and any subsequent calculation based on aNaNproduces anotherNaN. This helps improve performance in certain situations. For example, consider simulating paths of the underlier of a knock-out barrier option (that is, an option that becomes worthless when the price of the underlying asset crosses some prescribed barrier). Your end-of-period function could detect a barrier crossing and return aNaNto signal early termination of the current trial.
Optimizing Accuracy: About Solution Precision and Error
The simulation architecture does not, in general, simulate exact solutions to any SDE. Instead, the simulation architecture provides a discrete-time approximation of the underlying continuous-time process, a simulation technique often known as a Euler approximation.
In the most general case, a given simulation derives directly from an SDE. Therefore, the simulated discrete-time process approaches the underlying continuous-time process only in the limit as the time increment dt approaches zero. In other words, the simulation architecture places more importance on ensuring that the probability distributions of the discrete-time and continuous-time processes are close, than on the pathwise proximity of the processes.
Before illustrating techniques to improve the approximation of solutions, it is helpful to understand the source of error. Throughout this architecture, all simulation methods assume that model parameters are piecewise constant over any time interval of length dt. In fact, the methods even evaluate dynamic parameters at the beginning of each time interval and hold them fixed for the duration of the interval. This sampling approach introduces discretization error.
However, there are certain models for which the piecewise constant approach provides exact solutions:
Creating Brownian Motion (BM) Models with constant parameters, simulated by Euler approximation (
simByEuler).Creating Geometric Brownian Motion (GBM) Models with constant parameters, simulated by closed-form solution (
simBySolution).Creating Hull-White/Vasicek (HWV) Gaussian Diffusion Models with constant parameters, simulated by closed-form solution (
simBySolution)
More generally, you can simulate the exact solutions for these models even if the parameters vary with time, if they vary in a piecewise constant way such that parameter changes coincide with the specified sampling times. However, such exact coincidence is unlikely; therefore, the previously discussed constant parameter condition is commonly used in practice.
One obvious way to improve accuracy involves sampling the discrete-time process more frequently. This decreases the time increment (dt), causing the sampled process to more closely approximate the underlying continuous-time process. Although decreasing the time increment is universally applicable, however, there is a tradeoff among accuracy, run-time performance, and memory usage.
To manage this tradeoff, specify an optional input argument,
NSteps, for all simulation methods. NSteps
indicates the number of intermediate time steps within each time increment
dt, at which the process is sampled but not reported.
It is important and convenient at this point to emphasize the relationship of the
inputs NSteps, NPeriods, and
DeltaTime to the output vector Times,
which represents the actual observation times at which the simulated paths are reported.
NPeriods, a required input, indicates the number of simulation periods of lengthDeltaTime, and determines the number of rows in the simulated three-dimensionalPathstime series array (if an output is requested).DeltaTimeis optional, and indicates the correspondingNPeriods-length vector of positive time increments between successive samples. It represents the familiar dt found in stochastic differential equations. IfDeltaTimeis unspecified, the default value of 1 is used.NStepsis also optional, and is only loosely related toNPeriodsandDeltaTime.NStepsspecifies the number of intermediate time steps within each time incrementDeltaTime.Specifically, each time increment
DeltaTimeis partitioned intoNStepssubintervals of lengthDeltaTime/NStepseach, and refines the simulation by evaluating the simulated state vector at(NSteps - 1)intermediate times. Although the output state vector (if requested) is not reported at these intermediate times, this refinement improves accuracy by causing the simulation to more closely approximate the underlying continuous-time process. IfNStepsis unspecified, the default is1(to indicate no intermediate evaluation).The output
Timesis anNPeriods + 1-length column vector of observation times associated with the simulated paths. Each element ofTimesis associated with a corresponding row ofPaths.
The following example illustrates this intermediate sampling by
comparing the difference between a closed-form solution and a sequence of Euler
approximations derived from various values of NSteps.
Improve Solution Accuracy
Consider a univariate geometric Brownian motion (GBM) model using gbm with constant parameters:
Assume that the expected rate of return and volatility parameters are annualized, and that a calendar year comprises 250 trading days.
Use simBySolution to simulate approximately four years of univariate prices for both the exact solution and the Euler approximation (using simByEuler) for various values of NSteps.
nPeriods = 1000; dt = 1/250; obj = gbm(0.1,0.4,'StartState',100); rng(575,'twister') [X1,T1] = simBySolution(obj,nPeriods,'DeltaTime',dt); rng(575,'twister') [Y1,T1] = simByEuler(obj,nPeriods,'DeltaTime',dt); rng(575,'twister') [X2,T2] = simBySolution(obj,nPeriods,'DeltaTime', ... dt,'nSteps',2); rng(575,'twister') [Y2,T2] = simByEuler(obj,nPeriods,'DeltaTime', ... dt,'nSteps',2); rng(575,'twister') [X3,T3] = simBySolution(obj,nPeriods, 'DeltaTime', ... dt,'nSteps',10); rng(575,'twister') [Y3,T3] = simByEuler(obj,nPeriods,'DeltaTime', ... dt,'nSteps',10); rng(575,'twister') [X4,T4] = simBySolution(obj,nPeriods,'DeltaTime', ... dt,'nSteps',100); rng(575,'twister') [Y4,T4] = simByEuler(obj,nPeriods,'DeltaTime', ... dt,'nSteps',100);
Compare the error (the difference between the exact solution and the Euler approximation) graphically.
clf; plot(T1,X1 - Y1,'red') hold on; plot(T2,X2 - Y2,'blue') plot(T3,X3 - Y3,'green') plot(T4,X4 - Y4,'black') hold off xlabel('Time (Years)') ylabel('Price Difference') title('Exact Solution Minus Euler Approximation') legend({'# of Steps = 1' '# of Steps = 2' ... '# of Steps = 10' '# of Steps = 100'}, ... 'Location', 'Best') hold off
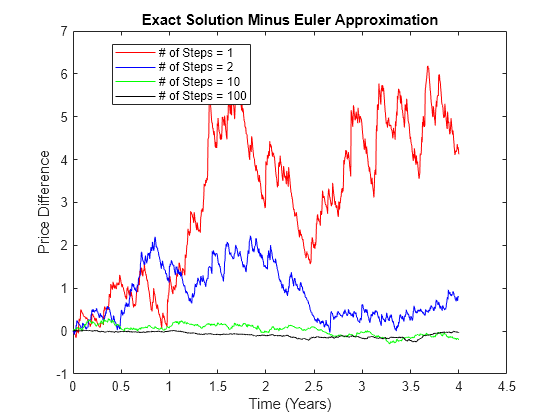
As expected, the simulation error decreases as the number of intermediate time steps increases. Because the intermediate states are not reported, all simulated time series have the same number of observations regardless of the actual value of NSteps.
Furthermore, since the previously simulated exact solutions are correct for any number of intermediate time steps, additional computations are not needed for this example. In fact, this assessment is correct. The exact solutions are sampled at intermediate times to ensure that the simulation uses the same sequence of Gaussian random variates in the same order. Without this assurance, there is no way to compare simulated prices on a pathwise basis. However, there might be valid reasons for sampling exact solutions at closely spaced intervals, such as pricing path-dependent options.
See Also
sde | bm | gbm | merton | bates | drift | diffusion | sdeddo | sdeld | cev | cir | heston | hwv | sdemrd | rvm | roughbergomi | roughheston | ts2func | simulate | simByEuler | interpolate | simByQuadExp | simBySolution | simBySolution
Topics
- Simulating Equity Prices
- Simulating Interest Rates
- Price American Basket Options Using Standard Monte Carlo and Quasi-Monte Carlo Simulation
- Improving Performance of Monte Carlo Simulation with Parallel Computing
- Base SDE Models
- Drift and Diffusion Models
- Linear Drift Models
- Parametric Models
- SDEs
- SDE Models
- SDE Class Hierarchy